20 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 8 Bài 5: Trường hợp đồng dạng thứ nhất của tam giác

Câu 1:

21/07/2024

ΔABC ~ ΔDEF theo tỉ số k₁, ΔMNP ~ ΔDEF theo tỉ số k₂. ΔABC ~ ΔMNP theo tỉ số nào?

A. k₁

B. $\frac{k_{2}}{k_{1}}$

C. k₁k₂

D. $\frac{k_{1}}{k_{2}}$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Vì ΔABC ~ ΔDEF theo tỉ số k₁, ΔMNP ~ ΔDEF theo tỉ số k₂nên

ta có $\frac{A B}{D E} = k_{1}$ => AB = k₁.DE

và $\frac{M N}{D E} = k_{2}$ => MN = k₂.DE

Từ đó ta có $\frac{A B}{M N} = \frac{k_{1} . D E}{k_{2} . D E} = \frac{k_{1}}{k_{2}}$

Câu 2:

17/07/2024

Một tam giác có cạnh nhỏ nhất bằng 8, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 27, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng.

A. x = 5; y = 10

B. x = 6; y = 12

C. x = 12; y = 18

D. x = 6; y = 18

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Tam giác thứ nhất có các cạnh là 8 < x < y

Tam giác thứ hai có các cạnh là x < y < 27

Vì hai tam giác đồng dạng nên $\frac{8}{x} = \frac{x}{y} = \frac{y}{27}$

ta có x.y = 8.27 và x² = 8y.

Do đó x² = 8y = 8. $\frac{8.27}{x}$ nên x³ = 64.27 = (4.3)³

Vậy x = 12, y = 18

Câu 3:

15/07/2024

Cho ΔABC đồng dạng với ΔMNP. Biết AB = 2cm, BC = 3cm, MN = 6cm, MP = 6cm. Hãy chọn khẳng định sai:

A. AC = 2cm

B. NP = 9cm

C. ΔMNP cân tại M

D. ΔABC cân tại C

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Vì ΔABC đồng dạng với ΔMNP

nên $\frac{A B}{M N} = \frac{A C}{M P} = \frac{B C}{N P}$ hay $\frac{2}{6} = \frac{A C}{6} = \frac{3}{N P}$

=> AC = $\frac{2.6}{6}$ = 2; NP = $\frac{6.3}{2}$ = 9

Vậy NP = 9cm, AC = 2cm nên A, B đúng.

Tam giác ABC cân tại A, MNP cân tại M nên C đúng, D sai.

Câu 4:

15/07/2024

Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Chọn câu đúng?

A. ΔA’B’C’ ~ ΔABC theo tỉ số k = $\frac{1}{2}$

B. ΔEDF ~ ΔABC theo tỉ số k = $\frac{1}{2}$

C. ΔA’B’C’ ~ ΔABC theo tỉ số k = $\frac{1}{2}$

D. ΔA’B’C’ ~ ΔEDF theo tỉ số k = $\frac{1}{2}$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

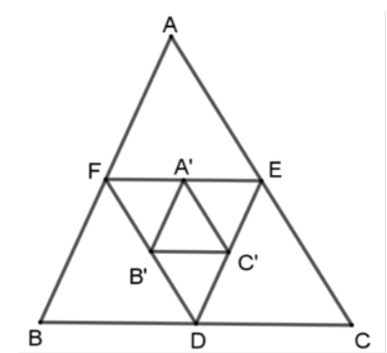
Vì D, E, F theo thứ tự làm trung điểm của BC, CA, AB nên EF, ED, FD là các đường trung bình của tam giác ABC nên $\frac{E F}{B C} = \frac{F D}{A C} = \frac{E D}{A B} = \frac{1}{2}$

suy ra ΔABC ~ ΔDEF (c - c - c) theo tỉ số đồng dạng k = 2.

Tương tự ta có A’B’, B’C’, C’A’ là các đường trung bình của tam giác DEF

nên ΔA’B’C’ ~ ΔDEF theo tỉ số k = $\frac{1}{2}$

Theo tính chất đường trung bình $\frac{B' C}{E F} = \frac{1}{2}$

mà $\frac{E F}{B C} = \frac{1}{2}$ (cmt) suy ra $\frac{B' C'}{B C} = \frac{1}{4}$

Tương tự $\frac{A' B'}{A B} = \frac{A' C'}{A C} = \frac{1}{4}$

Do đó ΔA’B’C’ ~ ΔABC theo tỉ số k = $\frac{1}{4}$

Câu 5:

17/07/2024

Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:

A. 2cm, 3cm, 4cm và 10cm, 15cm, 20cm.

B. 3cm, 4cm, 6cm và 9cm, 12cm, 16cm

C. 2cm, 2cm, 2cm và 1cm, 1cm, 1cm

D. 14cm, 15cm, 16cm và 7cm, 7,5cm, 8cm

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Ta thấy

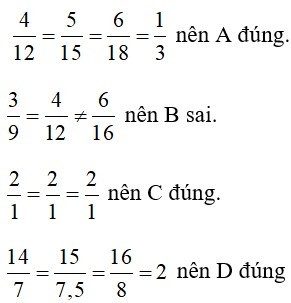
Câu 6:

15/07/2024

ΔDEF ~ ΔABC theo tỉ số k₁, ΔMNP ~ ΔDEF theo tỉ số k₂. ΔABC ~ ΔMNP theo tỉ số nào?

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Vì ΔDEF ~ ΔABC theo tỉ số k₁, ΔMNP ~ ΔDEF theo tỉ số k₂nên

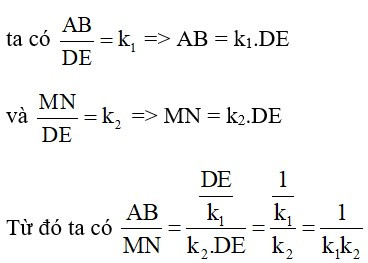
Câu 7:

23/07/2024

Cho 2 tam giác RSK và PQM có $\frac{R S}{M P} = \frac{R K}{P Q} = \frac{K S}{M Q}$ , khi đó ta có:

A. ΔRSK ~ ΔPQM

B. ΔRSK ~ ΔQPM

C. ΔRSK ~ ΔPMQ

D. ΔRSK ~ ΔQMP

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

2 tam giác RSK và PQM có $\frac{R S}{M P} = \frac{R K}{P Q} = \frac{K S}{M Q}$ ,

khi đó ta có: ΔRSK ~ ΔPMQ

Câu 8:

23/07/2024

Một tam giác có cạnh nhỏ nhất bằng 12, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 40,5, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng, từ đó suy ra giá trị của S = x + y bằng:

A. 45

B. 60

C. 55

D. 35

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Tam giác thứ nhất có các cạnh là 12 < x < y

Tam giác thứ hai có các cạnh là x < y < 40,5

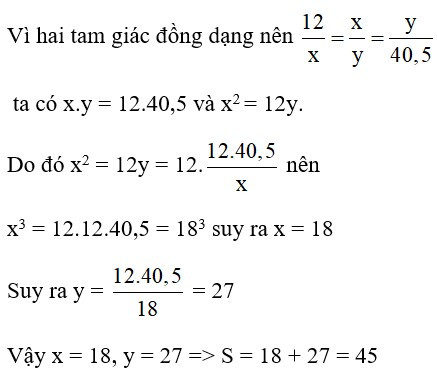
Câu 9:

15/07/2024

Cho ΔABC ~ ΔIKH. Số khẳng định sai trong các khẳng định trên là:

A. 0

B. 1

C. 2

D. 3

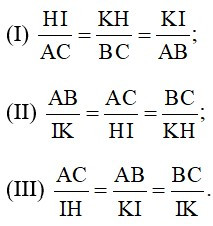
Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Vì ΔABC ~ ΔIKH nên $\frac{A B}{I K} = \frac{B C}{K H} = \frac{A C}{I H}$

hay $\frac{I K}{A B} = \frac{K H}{B C} = \frac{I H}{A C}$ nên (I) và (II) đúng, (III) sai.

Do đó chỉ có 1 khẳng định sai.

Câu 10:

23/07/2024

Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE.

1. ΔABD đồng dạng với tam giác nào dưới đây?

A. ΔAEG

B. ΔABC

C. Cả A và B

D. Không có tam giác nào

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

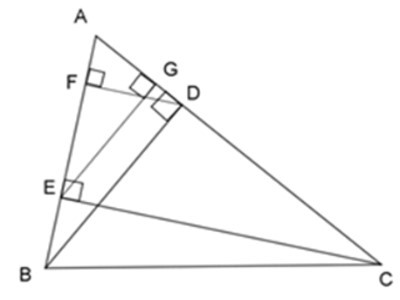
Xét ΔABD và ΔAEG, ta có:

BD ⊥ AC (BD là đường cao)

EG ⊥ AC (EG là đường cao)

=> BD // EG

Theo định lý Talet, ta có: $\frac{A E}{A B} = \frac{A G}{A D} = \frac{E G}{B D}$

=> ΔAEG ~ ΔABD (c - c - c) (đpcm)

Câu 11:

23/07/2024

Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE.

Chọn khẳng định đúng?

A. AD.AE = AB.AF

B. AD.AE = AB.AG = AC.AF

C. AD.AE = AC.GA

D. AD.AE = AB.AF = AC.AG

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

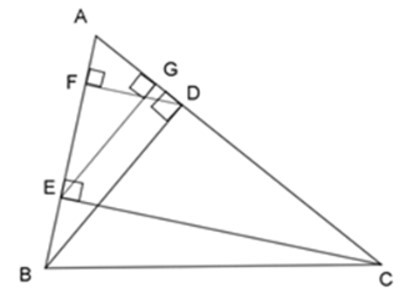
Từ câu trước ta có:

$\frac{A E}{A B} = \frac{A G}{A D}$

=> AE.AD = AB.AG (1)

Chứng minh tương tự, ta được:

ΔAFD ~ ΔAEC (c - c - c)

=> $\frac{A F}{A E} = \frac{A D}{A C}$

=> AF.AC = AE.AD (2)

Từ (1) và (2) ta có:

AD.AE = AB.AG = AC.AF

Câu 12:

20/07/2024

Tứ giác ABCD có AB = 8cm, BC = 15cm, CD = 18cm, AD = 10cm, BD = 12cm. Chọn câu đúng nhất:

A. ΔABD ~ ΔBDC

B. ABCD là hình thang

C. ABCD là hình thang vuông

D. Cả A, B đều đúng

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

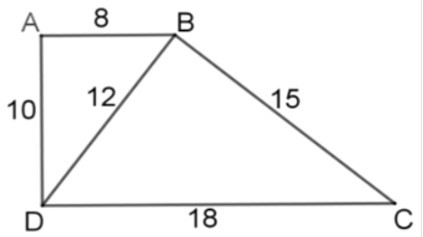
Ta có: $\frac{A B}{B D} = \frac{A D}{B C} = \frac{B D}{D C}$

(vì $\frac{8}{12} = \frac{10}{15} = \frac{12}{18} (= \frac{2}{3})$ )

Nên ΔABD ~ ΔBDC (c - c - c)

ΔABD ~ ΔBDC nên góc ABD = BDC.

Mà hai góc này ở vị trí so le trong nên AB // CD.

Vậy ABCD là hình thang.

Lại có BD² = 144 < 164 = AD² + AB² nên ΔABD không vuông. Do đó ABCD không là hình thang vuông

Vậy A, B đều đúng, C sai.

Câu 13:

15/07/2024

Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:

A. 4cm, 5cm, 6cm và 12cm, 15cm, 18cm.

B. 3cm, 4cm, 6cm và 9cm, 12cm, 18cm

C. 1,5cm, 2cm, 2cm và 1cm, 1cm, 1cm

D. 14cm, 15cm, 16cm và 7cm, 7,5cm, 8cm

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Ta thấy

$\frac{4}{12} = \frac{5}{15} = \frac{6}{18} = \frac{1}{3}; \frac{3}{9} = \frac{4}{12} = \frac{6}{18} = \frac{1}{3}$

và

$\frac{14}{7} = \frac{15}{7,5} = \frac{16}{8} = 2; \frac{1,5}{2} \neq \frac{2}{1} = \frac{2}{1}$

nên C sai.

Câu 14:

15/07/2024

Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Xét các khẳng định sau:

(I) ΔEDF ~ ΔABC theo tỉ số k = $\frac{1}{2}$

(II) ΔA’B’C’ ~ ΔABC theo tỉ số k = $\frac{1}{4}$

(III) ΔA’B’C’ ~ ΔEDF theo tỉ số k = 2

Số khẳng định đúng là:

A. 2

B. 1

C. 3

D. 0

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

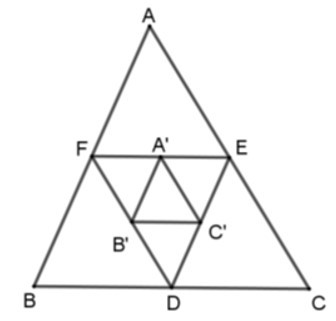
Vì D, E, F theo thứ tự làm trung điểm của BC, CA, AB nên EF, ED, FD là các đường trung bình của tam giác ABC nên $\frac{E F}{B C} = \frac{F D}{A C} = \frac{E D}{A B} = \frac{1}{2}$

suy ra ΔEDF ~ ΔABC (c - c - c) theo tỉ số đồng dạng

k = $\frac{1}{2}$ hay (I) đúng.

Tương tự ta có A’B’, B’C’, C’A’ là các đường trung bình của tam giác DEF

nên ΔA’B’C’ ~ ΔDEF theo tỉ số k = $\frac{1}{2}$ nên (III) sai

Theo tính chất đường trung bình

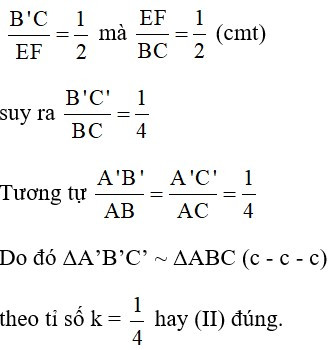
Do đó có 2 khẳng định đúng

Câu 15:

15/07/2024

Cho 2 tam giác RSK và PQM có $\frac{R S}{P Q} = \frac{R K}{P M} = \frac{S K}{Q M}$ , khi đó ta có

A. ΔRSK ~ ΔPQM

B. ΔRSK ~ ΔQPM

C. ΔRSK ~ ΔMPQ

D. ΔRSK ~ ΔQMP

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

2 tam giác RSK và PQM có $\frac{R S}{P Q} = \frac{R K}{P M} = \frac{S K}{Q M}$ , khi đó ta có: ΔRSK ~ ΔPQM

Câu 16:

15/07/2024

Cho ΔABC ~ ΔIKH. Có bao nhiêu khẳng định đúng trong các khẳng định sau:

A. 0

B. 1

C. 2

D. 3

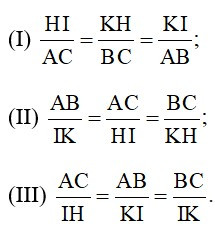
Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Vì ΔABC ~ ΔIKH nên $\frac{A B}{I K} = \frac{B C}{K H} = \frac{A C}{I H}$

hay $\frac{I K}{A B} = \frac{K H}{B C} = \frac{I H}{A C}$ nên (I) và (II) đúng, (III) sai.

Câu 17:

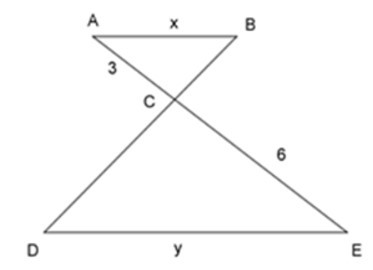
22/07/2024

Cho tam giác ΔABC ~ ΔEDC như hình vẽ, tỉ số độ dài của x và y là:

A. 7

B. $\frac{1}{2}$

C. $\frac{7}{4}$

D. $\frac{7}{16}$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Ta có: ΔABC ~ ΔEDC

=> $\frac{A B}{E D} = \frac{A C}{E C} \Leftrightarrow \frac{x}{y} = \frac{3}{6} = \frac{1}{2}$

Câu 18:

15/07/2024

Tứ giác ABCD có AB = 9cm, BC = 20cm, CD = 25cm, AD = 12cm, BD = 15cm. Chọn câu sai:

A. ΔABD ~ ΔBDC

B. ABCD là hình thang

C. ABCD là hình thang vuông

D. ABCD là hình thang cân

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

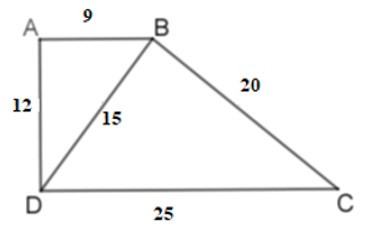
Ta có: $\frac{A B}{B D} = \frac{A D}{B C} = \frac{B D}{D C}$

(vì $\frac{9}{15} = \frac{12}{20} = \frac{15}{25} (= \frac{3}{3})$ )

Nên ΔABD ~ ΔBDC (c - c - c)

ΔABD ~ ΔBDC nên góc ABD = BDC.

Mà hai góc này ở vị trí so le trong nên AB // CD.

Vậy ABCD là hình thang.

Lại có BD² = 225 = AD² + AB² nên ΔABD vuông tại A. Do đó ABCD là hình thang vuông

Vậy A, B, C đều đúng, D sai

Câu 19:

17/07/2024

Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE.

1. Xét các cặp tam giác sau đây, số cặp tam giác đồng dạng với nhau là:

(1) ΔAEG và ΔABD

(2) ΔADF và ΔACE

(3) ΔABC và ΔAEC

A. 1

B. 0

C. 2

D. 3

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

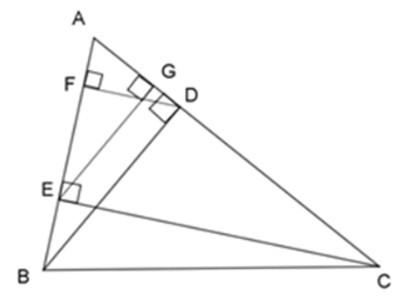
Xét ΔABD và ΔAEG, ta có:

BD ⊥ AC (BD là đường cao)

EG ⊥ AC (EG là đường cao)

=> BD // EG

Theo định lý Talet, ta có: $\frac{A E}{A B} = \frac{A G}{A D} = \frac{E G}{B D}$

=> ΔAEG ~ ΔABD (c - c - c) nên (1) đúng.

Tương tự ta cũng chứng minh được ΔADF ~ ΔACE nên (2) đúng

Dễ thấy (3) sai vì $\frac{A E}{A B} \neq \frac{A C}{A C}$

Vậy có hai cặp tam giác đồng dạng trong các cặp đã nêu.

Câu 20:

20/07/2024

Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE.

2. Chọn khẳng định không đúng?

A. AD.AE = AB.AFG

B. AD.AE = AC.AF

C. AD.AE = AC.FD

D. AE.EG = AB.BD

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

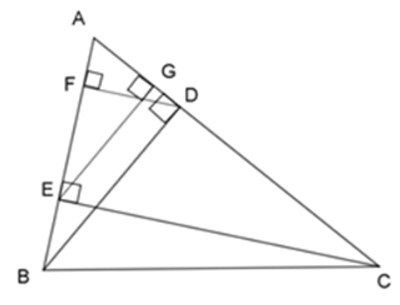
Từ câu trước ta có: $\frac{A E}{A B} = \frac{A G}{A D} = \frac{E G}{B D}$

=> AE.AD = AB.AG (1) nên A đúng

Chứng minh tương tự, ta được:

ΔAFD ~ ΔAEC (c - c - c)

=> $\frac{A F}{A E} = \frac{A D}{A C}$

=> AF.AC = AE.AD (2) nên B đúng

Ngoài ra $\frac{A D}{A C} = \frac{F D}{E C}$

=> AD.EC = AC.FD nên C đúng

Chỉ có đáp án D sai vì $\frac{A E}{E G} = \frac{A B}{B D}$

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3