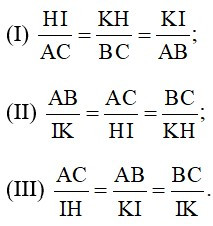Câu hỏi:
23/07/2024 176Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE.
1. ΔABD đồng dạng với tam giác nào dưới đây?
A. ΔAEG
B. ΔABC
C. Cả A và B
D. Không có tam giác nào
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: A
Giải thích:
Lời giải
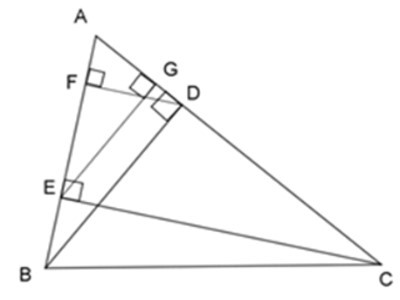
Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lý Talet, ta có:
=> ΔAEG ~ ΔABD (c - c - c) (đpcm)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE.
Chọn khẳng định đúng?
Câu 2:
Cho ΔABC đồng dạng với ΔMNP. Biết AB = 2cm, BC = 3cm, MN = 6cm, MP = 6cm. Hãy chọn khẳng định sai:
Câu 3:
ΔDEF ~ ΔABC theo tỉ số k1, ΔMNP ~ ΔDEF theo tỉ số k2. ΔABC ~ ΔMNP theo tỉ số nào?
Câu 4:
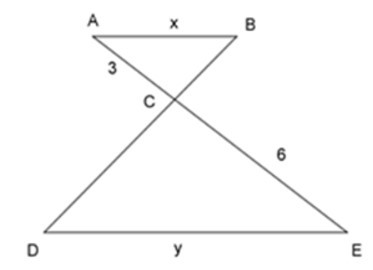
Cho tam giác ΔABC ~ ΔEDC như hình vẽ, tỉ số độ dài của x và y là:
Câu 7:
Một tam giác có cạnh nhỏ nhất bằng 8, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 27, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng.
Câu 8:
Tứ giác ABCD có AB = 8cm, BC = 15cm, CD = 18cm, AD = 10cm, BD = 12cm. Chọn câu đúng nhất:
Câu 9:
Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Chọn câu đúng?
Câu 10:
Cho ΔABC ~ ΔIKH. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
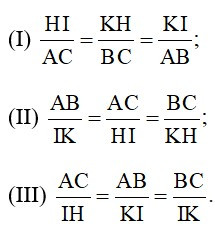
Câu 11:
Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
Câu 12:
Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Xét các khẳng định sau:
(I) ΔEDF ~ ΔABC theo tỉ số k =
(II) ΔA’B’C’ ~ ΔABC theo tỉ số k =
(III) ΔA’B’C’ ~ ΔEDF theo tỉ số k = 2
Số khẳng định đúng là:
Câu 13:
Tứ giác ABCD có AB = 9cm, BC = 20cm, CD = 25cm, AD = 12cm, BD = 15cm. Chọn câu sai:
Câu 14:
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE.
2. Chọn khẳng định không đúng?
Câu 15:
Một tam giác có cạnh nhỏ nhất bằng 12, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 40,5, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng, từ đó suy ra giá trị của S = x + y bằng: