Trắc nghiệm Toán 8 Bài 2: Định lý đảo và hệ quả của định lý Ta-let
-
316 lượt thi
-
18 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Cho hình vẽ. Điều kiện nào sau đây không suy ra được DE // BC?
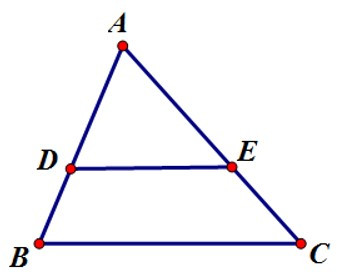
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Theo định lý đảo của định lý Ta-lét. Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Dễ thấy, từ các điều kiện
Dễ thấy, từ các điều kiện
; ; ta đều suy ra được DE // BC.
Chỉ có D sai.
Câu 2:
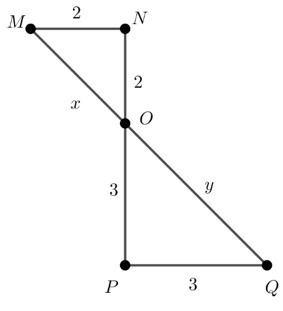
23/07/2024Tính các độ dài x, y trong hình bên:
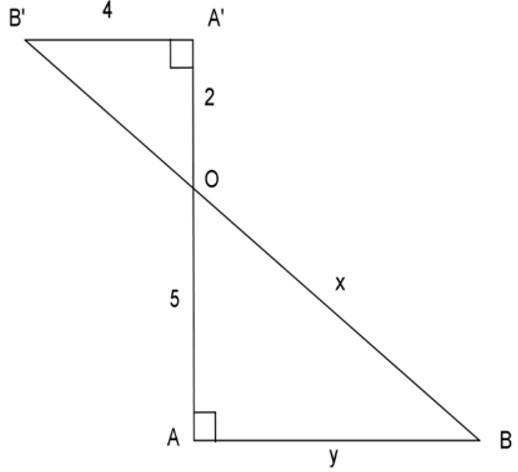
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Áp dụng định lý Py-ta-go cho tam giác vuông OA’B’,
ta có: OA’2 + A’B’2 = OB’2
Câu 3:
23/07/2024Chọn câu trả lời đúng:
Cho hình thang ABCD (AB // CD), O là giao điểm của AC và BD. Xét các khẳng định sau:
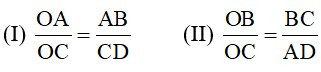
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
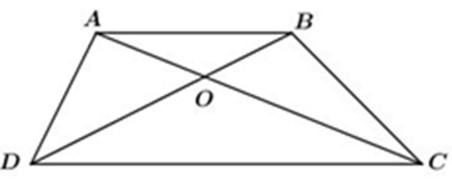
Vì AB // CD, áp dụng hệ quả định lý Talet,
Câu 4:
16/07/2024Cho hình thang ABCD (AB // CD) có diện tích 36cm2, AB = 4cm, CD = 8cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD.
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
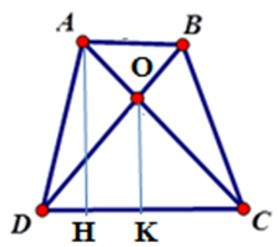
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang:
Câu 5:
23/07/2024Cho hình vẽ, Có bao nhiêu cặp đường thẳng song song
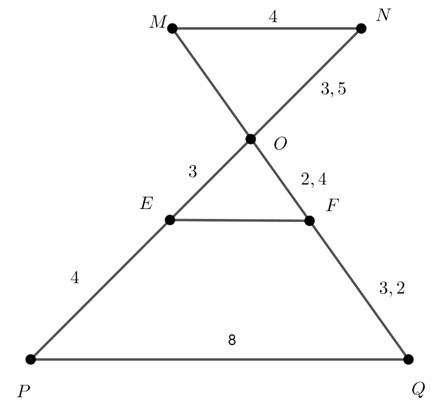
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Câu 6:
23/07/2024Cho hình thang ABCD (AB // CD) có diện tích 48cm2, AB = 4cm, CD = 8cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD.
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
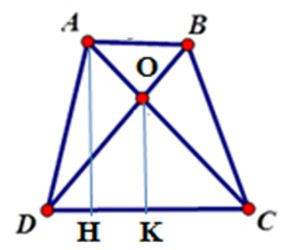
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang:
Câu 7:
14/07/2024Cho hình thang ABCD (AB // CD) có diện tích 48cm2, AB = 4cm, CD = 8cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD.
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang:
Câu 8:
23/07/2024hãy chọn câu sai. Cho hình vẽ với AB < AC:
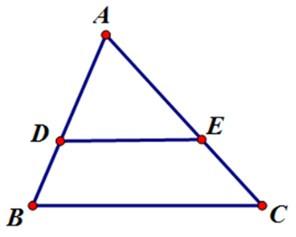
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Theo định lý đảo của định lý Ta-lét. Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Nên D sai.
Câu 9:
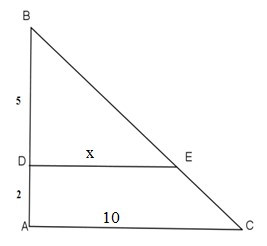
23/07/2024Cho hình vẽ. Tìm x (làm tròn kết quả đến chữ thập phân thứ hai)
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có: AB = BD + AD = 5 + 2 = 7
Vì DE // AC, áp dụng hệ quả của định lý Talet, ta có:
Câu 10:
23/07/2024Cho tam giác ABC có AB = 9cm, điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E Є AC), kẻ EF song song với CD (F Є AB). Tính độ dài AF.
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
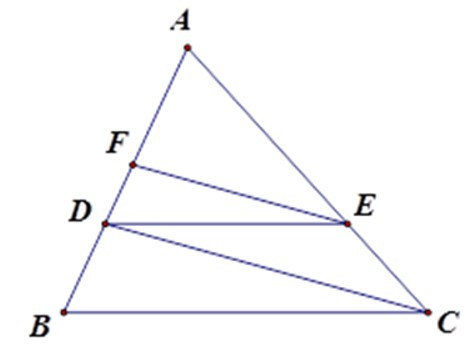
Áp dụng định lý Ta-lét:
Câu 11:
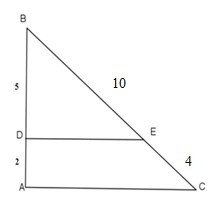
17/07/2024Cho hình vẽ. Hai đường thẳng nào dưới đây song song
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có :
Theo định lý đảo của định lý Talet, ta suy ra DE//AC
Câu 12:
23/07/2024Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB và AC theo thứ tự tại D và E. Qua E kẻ đường thẳng song song với CD, cắt AB ở F. Biết AB = 16, AF = 9, độ dài AD là:
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
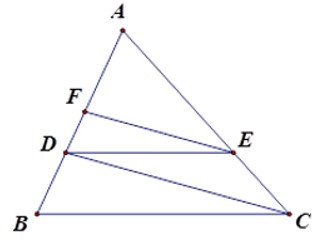
Áp dụng định lý Ta-lét:
Câu 13:
22/07/2024Cho hình vẽ sau :
Phát biểu nào dưới đây là đúng
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có :
Câu 14:
23/07/2024Cho điểm M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM.
1. Đặt MA = a, MB = b. Tính ME, MF theo a và b.
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
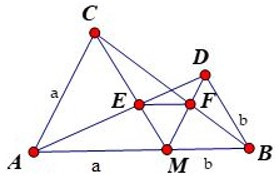
Vì các tam giác AMC và BMD đều
Câu 15:
23/07/2024Cho điểm M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM.
Tam giác MEF là tam giác gì? Chọn đáp án đúng nhất?
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
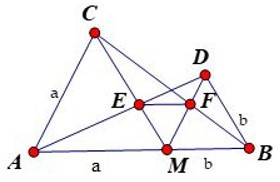
Câu 16:
23/07/2024Cho hình thang ABCD (AB // CD) có diện tích 36cm2, AB = 4cm, CD = 8cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD.
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
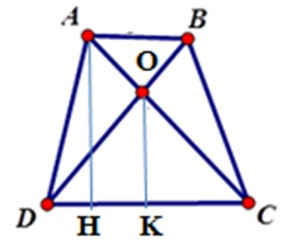
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang:
Câu 17:
22/07/2024Cho điểm M thuộc đoạn thẳng AB sao cho MA = 2MB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM.
1. Đặt MB = a. Tính ME, MF theo a.
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
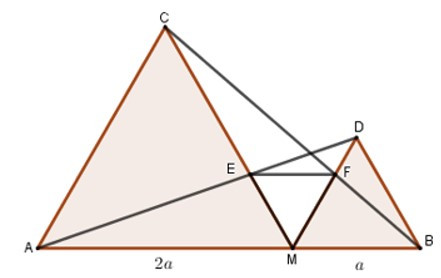
Đặt MB = a => MA = 2a
Vì các tam giác AMC và BMD đều
nên = 600 (hai góc ở vị trí đồng vị)
=> MD // AC
Vì MD // AC nên theo hệ quả định lý Talet cho hai tam giác DEM và AEC ta có
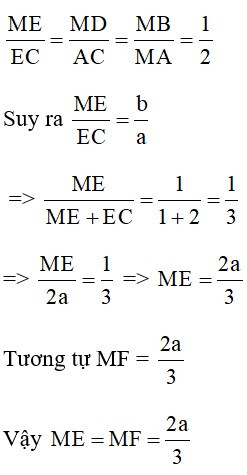
Câu 18:
23/07/2024Cho điểm M thuộc đoạn thẳng AB sao cho MA = 2MB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM.
Chọn khẳng định đúng nhất.
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
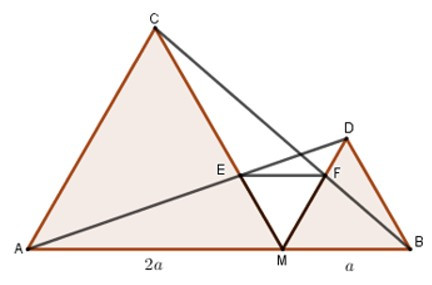
Từ câu 1) ta có ME = MF
=> ΔEMF cân tại M
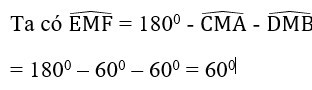
Từ đó MEF là tam giác cân có một góc bằng 600 nên nó là tam giác đều
Vậy EF = ME = MF =