Trắc nghiệm Toán 8 Bài 6: Trường hợp đồng dạng thứ hai của tam giác
-
332 lượt thi
-
19 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Để hai tam giác ABC và EDF đồng dạng thì số đo góc D trong hình vẽ dưới bằng:
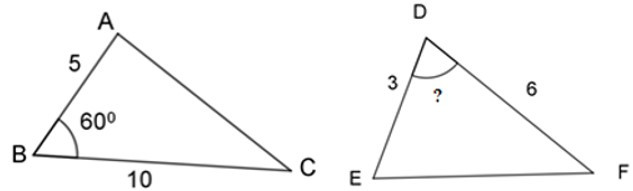
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
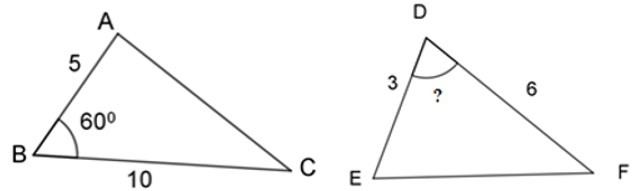
Có:
Để hai tam giác đã cho đồng dạng thì góc ABC = EDF = 600.
Câu 2:
21/07/2024Với AB // CD thì giá trị của x trong hình vẽ dưới đây là
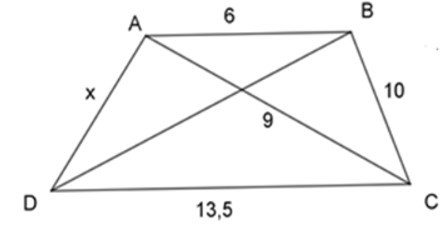
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
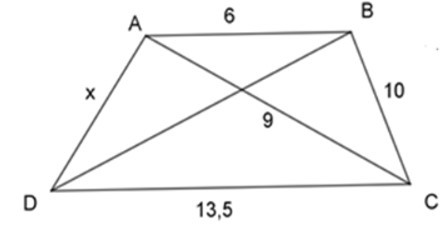
Ta có:
Câu 3:
22/07/2024Cho hình vẽ dưới đây, tính giá trị của x?
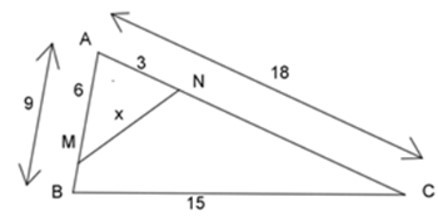
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
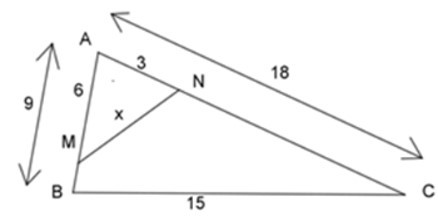
Ta có:
Câu 4:
20/07/2024Cho tam giác ABC có AB = 8cm, AC = 16cm.
Điểm D thuộc cạnh AB sao cho BD = 2cm.
Điểm E thuộc cạnh AC sao cho CE = 13cm.
1. Chọn câu đúng.
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
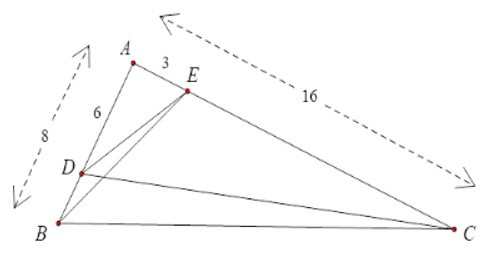
Ta có:
Xét ΔAED và ΔABC có A chung
và (cmt)
Nên ΔAED ~ ΔABC (c.g.c)
Câu 5:
22/07/2024Cho tam giác ABC có AB = 8cm, AC = 16cm.
Điểm D thuộc cạnh AB sao cho BD = 2cm.
Điểm E thuộc cạnh AC sao cho CE = 13cm.
2. Chọn câu sai.
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
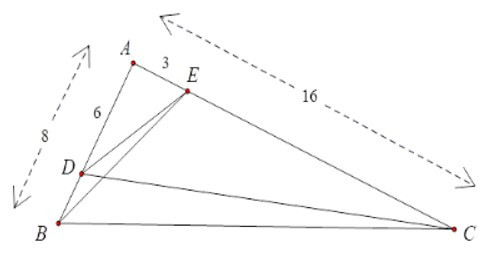
+ Xét ΔABE và ΔACD có A chung
và nên
ΔABE ~ ΔACD (c - g - c)
suy ra góc (hai góc tương ứng)
và
=> AE.CD = AD.BE
+ ΔAED ~ ΔABC (cmt)
nên
AE.AC = AB.AD
Nên A, C, D đúng, B sai.
Câu 6:
14/07/2024Cho tam giác ABC có AB = 12cm, AC = 18cm, BC = 27cm. Điểm D thuộc cạnh BC sao cho CD = 12cm. Tính độ dài AD.
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
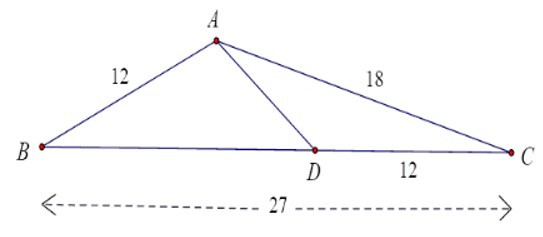
Ta có
Câu 7:
22/07/2024Cho tam giác nhọn ABC có C = 400. Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của các tam giác ABC, ACD. Tính số đo góc AKH.
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
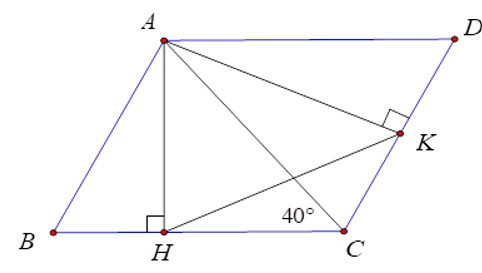
Vì AD.AH = AB.AK (=SABCD)
Câu 8:
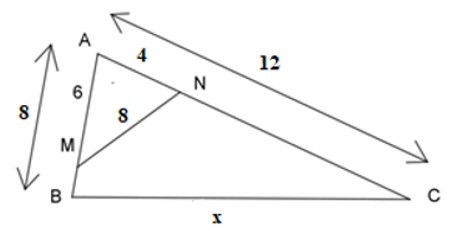
18/07/2024Cho hình vẽ dưới đây, tính giá trị của x?
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
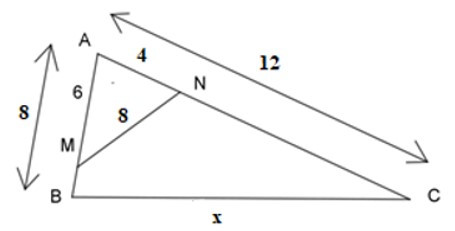
Ta có:
Câu 9:
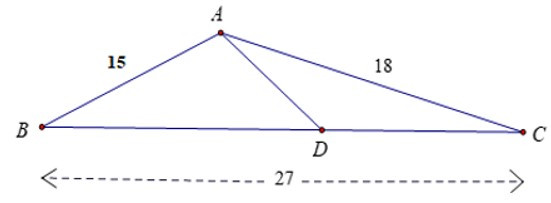
16/07/2024Cho tam giác ABC có AB = 15cm, AC = 18cm, BC = 27cm. Điểm D
thuộc cạnh BC sao cho . Độ dài AD là:
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Câu 10:
14/07/2024Cho hình thang vuông ABCD (A = D = 900) có AB = 16cm, CD = 25cm, BD = 20cm.
1. Tam giác ABD đồng dạng với tam giác nào dưới đây?
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
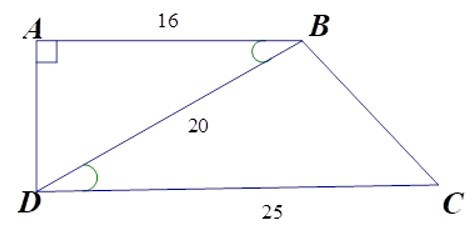
ΔABD và ΔBDC có góc ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD);
Và (vì )
Do đó ΔABD ~ ΔBDC (c.g.c)
Câu 11:
22/07/2024Cho hình thang vuông ABCD (A = D = 900) có AB = 16cm, CD = 25cm, BD = 20cm.
Độ dài cạnh BC là
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
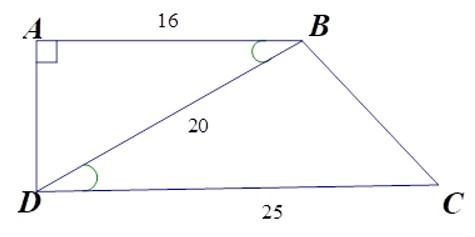
Vì ΔABD ~ ΔBDC (cmt) nên góc A = DBC.
Ta có A = 900 nên DBC = 900. Theo định lí Pytago, ta có
BC2 = CD2 - BD2 = 252 - 202 = 152.
Vậy BC = 15cm
Câu 12:
19/07/2024Cho hình thang ABCD có: AB // CD, AB = 4, CD = 16, AC = 8, AD = 12. Độ dài BC là:
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
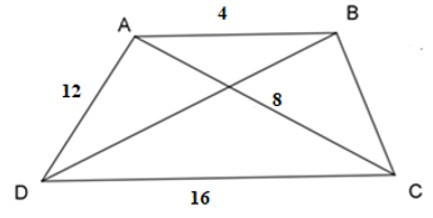
Ta có:
Câu 13:
20/07/2024Cho ΔABC, lấy 2 điểm D và E lần lượt nằm bên cạnh AB và AC
sao cho . Kết luận nào sai?
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
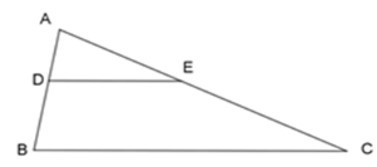
Xét ΔADE và ΔABC ta có:
Câu 14:
22/07/2024Cho hình thang vuông ABCD (A = D = 900)
có AB = 1cm, CD = 4cm, BD = 2cm.
1.Chọn kết luận sai?
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
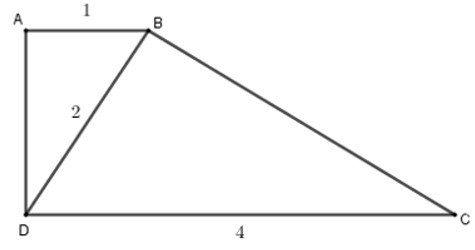
ΔABD và ΔBDC có: ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD)
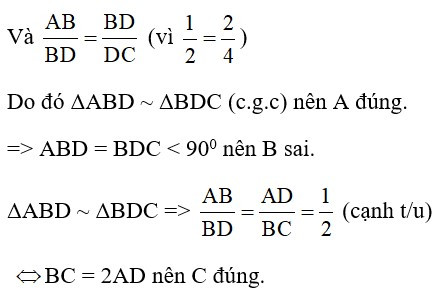
BAD = DBC = 900 nên BD BC hay D đúng
Vậy chỉ có B sai.
Câu 15:
17/07/2024Cho hình thang vuông ABCD (A = D = 900)
có AB = 1cm, CD = 4cm, BD = 2cm.
2. Độ dài cạn BC là (làm tròn đến hai chữ số thập phân)
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Tam giác BDC vuông tại B (theo câu trên), định lý Pitago ta có:
BD2 + BC2 = CD2
22 + BC2 = 42
BC2 = 12 => BC ≈ 3,46
Câu 16:
23/07/2024Hãy chọn câu đúng. Nếu ΔABC và ΔDEF
có góc B = D; thì:
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
ΔABC và ΔDEF có góc B = D;
thì ΔABC đồng dạng với ΔEDF
Câu 17:
14/07/2024Cho ΔABC và ΔDEF có góc B = E; , chọn kết luận đúng
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
ΔABC và ΔDEF có góc B = E; thì ΔABC đồng dạng với ΔDEF
Câu 18:
10/07/2024Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
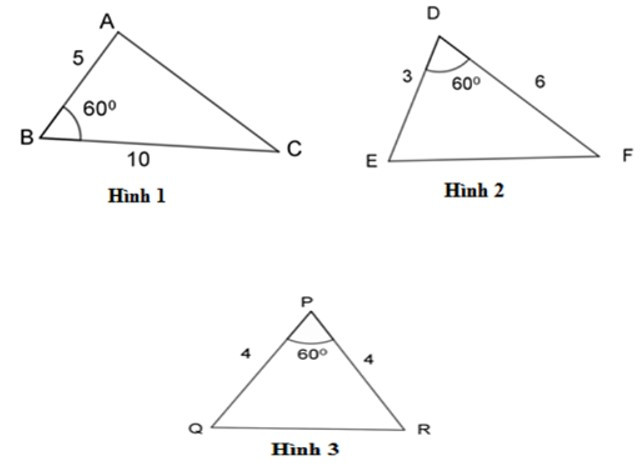
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
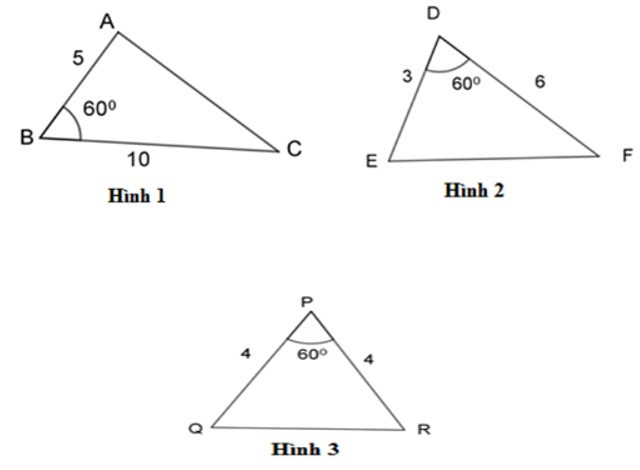
Có:
Xét ΔABC và ΔEDF ta có:
(cmt)
B = D = 600 (gt)
=> ΔABC ~ ΔEDF (c - g - c).
Câu 19:
15/07/2024Cho ΔABC, trên cạnh AB lấy điểm D khác A, B. Qua D kẻ đường thẳng song song với BC cắt AC tại E. Chọn kết luận sai?
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
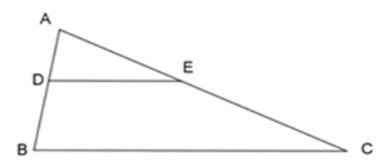
Do DE // BC nên theo định lý Talet đảo ta có nên C đúng.
Xét ΔADE và ΔABC ta có:
(cmt)
A chung.
=> ΔADE ~ ΔABC (c - g - c) nên A đúng
=> ADE = ABC (cặp góc tương ứng) nên D sai.