Dạng 3: Chứng minh các yếu tố hình học liên quan
-
417 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
16/07/2024Cho tam giác ABC, AB = 4 cm, AC = 6 cm, BC = 8 cm. Kéo dài AB lấy điểm D sao cho AB = BD, kéo dài AC lấy điểm E sao cho AC = CE, kéo dài trung tuyến AM của tam giác ABC lấy F sao cho AM = MF. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: C
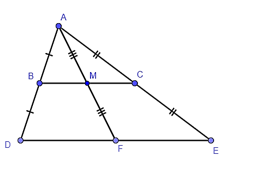
Vì AC = CE nên CE = 6 cm.
Từ giả thiết, ta có tam giác ADE có B là trung điểm của AD, C là trung điểm của AE.
Do đó BC là đường trung bình của tam giác ADE.
Suy ra BC=12DE , BC // DE (tính chất đường trung bình của tam giác).
Hay DE = 2BC = 2 ⋅ 8 = 16 (cm).
Trong tam giác ADF có B là trung điểm của AD, M là trung điểm của AF.
Do đó BM là đường trung bình của tam giác ADF.
Suy ra BM // DF (tính chất đường trung bình của tam giác).
Hay BC // DF (M ∈ BC).
Vì BC // DE và BC // DF nên D, E, F thẳng hàng.
Vậy đáp án C đúng.
Câu 2:
18/07/2024Cho tam giác MNP cân tại M có D là trung điểm của NP. Từ D kẻ DE song song với MP (E ∈ MN), kẻ DF song song với MN (F ∈ MP). Khi đó ME bằng với đoạn thẳng nào?
Xem đáp án
Đáp án đúng là: D
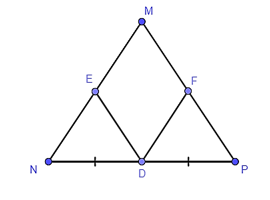
Trong tam giác MNP có:
+ D là trung điểm của NP, DE // MP, E ∈ MN.
Do đó E là trung điểm của MN (tính chất đường trung bình của tam giác).
Suy ra ME = EN = 12MN (1).
+ D là trung điểm của NP, DF // MN, F ∈ MP.
Do đó F là trung điểm của MP (tính chất đường trung bình của tam giác).
Suy ra MF = FP = 12 MP (2).
Mà tam giác MNP cân tại M nên MN = MP (3).
Từ (1), (2), (3) suy ra ME = EN = MF = FP.
Câu 3:
20/07/2024Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AC. Qua A kẻ Ax song song với BC cắt HI tại K. Khi đó HK song song với:
Xem đáp án
Đáp án đúng là: A
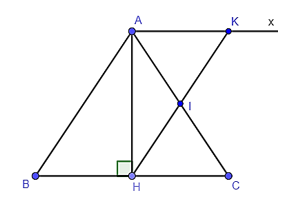
Vì tam giác ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến.
Suy ra H là trung điểm của BC.
Trong tam giác ABC có H là trung điểm của BC, I là trung điểm của AC.
Do đó HI là đường trung bình của tam giác ABC.
Suy ra HI // AB (tính chất đường trung bình của tam giác).
Vì K ∈ HI nên HK // AB.
Câu 4:
20/07/2024Cho tam giác OMN cân tại O. I là trung điểm của đường cao OH, NI cắt OM tại K. Từ H kẻ Hx song song với NK cắt OM tại D. Khi đó độ dài OM gấp mấy lần độ dài OK?
Xem đáp án
Đáp án đúng là: C
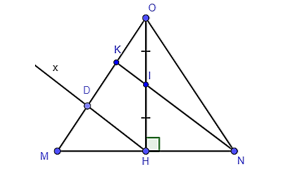
Vì tam giác OMN cân tại O nên OH vừa là đường cao vừa là đường trung tuyến.
Suy ra H là trung điểm của MN.
Trong tam giác MKN có H là trung điểm của MN, DH // KN, D ∈ MK.
Do đó D là trung điểm của MK.
Suy ra MD = DK (1).
Trong tam giác ODH có I là trung điểm của OH, KI // DH (do I ∈ NK), K ∈ OD.
Do đó K là trung điểm của OD.
Suy ra OK = DK (2).
Lại có OK + DK + MD = OM (3).
Từ (1), (2), (3) suy ra OM = 3OK.
Câu 5:
21/07/2024Cho tam giác ABC trên nửa mặt phẳng bờ AC không chứa điểm B lấy điểm D bất kì. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, AD, DC. Khi đó EF + FH + HG + GE bằng
Xem đáp án
Đáp án đúng là: C
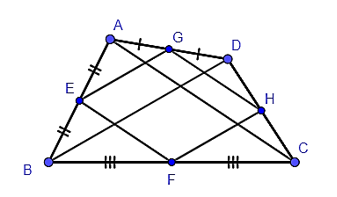
Trong tam giác ABD có E là trung điểm của AB, G là trung điểm của AD
Do đó EG là đường trung bình của tam giác ABD.
Suy ra EG=12BD (tính chất đường trung bình của tam giác).
Trong tam giác CBD có F là trung điểm của BC, H là trung điểm của CD
Do đó FH là đường trung bình của tam giác CBD.
Suy ra FH=12BD (tính chất đường trung bình của tam giác).
Trong tam giác ADC có H là trung điểm của DC, G là trung điểm của AD
Do đó HG là đường trung bình của tam giác ADC.
Suy ra HG=12AC (tính chất đường trung bình của tam giác).
Trong tam giác ABC có E là trung điểm của AB, F là trung điểm của BC
Do đó EF là đường trung bình của tam giác ABC.
Suy ra EF=12AC (tính chất đường trung bình của tam giác).
Ta có EF + FH + HG + GE = 12AC+12BD +12AC+12BD = AC + BD.
Câu 6:
16/07/2024Cho tam giác ABC đều, I là trung điểm BC. Từ I kẻ IK // AB (K ∈ AC), IH // AC (H ∈ AB). Tam giác IHK là tam giác gì?
Xem đáp án
Đáp án đúng là: A
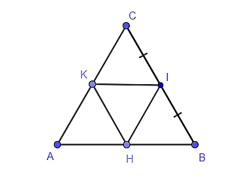
Trong tam giác ABC có I là trung điểm BC, HI // AC, H ∈ AB.
Do đó H là trung điểm của AB (tính chất đường trung bình của tam giác).
Suy ra HI là đường trung bình của tam giác ABC.
Nên HI=12AC (tính chất đường trung bình của tam giác).
Chứng minh tương tự ta có HK, IK là đường trung bình của tam giác ABC.
Nên HK=12BC, KI=12AB (tính chất đường trung bình của tam giác).
Vì tam giác ABC đều nên AB = AC = BC.
Suy ra HI = HK = KI.
Vậy tam giác HIK là tam giác đều.
Câu 7:
16/07/2024Cho tam giác MNP, trên MN lấy hai điểm D, E sao cho MD = DE = EN. Gọi I là trung điểm NP, PD cắt MI tại H. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: B
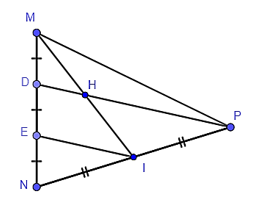
Trong tam giác NDP có I là trung điểm NP, E là trung điểm DN (DE = EN).
Do đó EI là đường trung bình của tam giác NDP.
Suy ra EI // PD và EI=12PD (tính chất đường trung bình của tam giác) (1).
Trong tam giác MEI có D là trung điểm ME (MD = DE), DH // EI (H ∈ DP).
Suy ra H là trung điểm của MI.
Nên HD là đường trung bình của tam giác MEI.
Suy ra HD=12EI (tính chất đường trung bình của tam giác) (2).
Từ (1) và (2) suy ra HD=13EI=12⋅12PD=14PD .
Câu 8:
20/07/2024Cho tam giác ABC vuông tại B, phân giác AD. Gọi M, N, I lần lượt là trung điểm của AD, AC, CD. Tứ giác BMNI là hình gì?
Xem đáp án
Đáp án đúng là: C
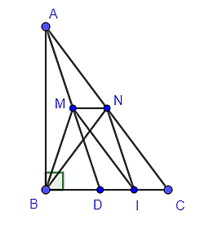
Trong tam giác ADC có M là trung điểm AD, N là trung điểm AC.
Do đó MN là đường trung bình của tam giác ADC.
Suy ra MN // DC (tính chất đường trung bình của tam giác).
Do đó, MN // BI. Suy ra tứ giác BMNI là hình thang.
Trong tam giác ADC có M là trung điểm AD, I là trung điểm DC.
Do đó MI là đường trung bình của tam giác ADC.
Suy ra MI=12AC (tính chất đường trung bình của tam giác) (1).
Trong tam giác ABC vuông tại B, có BN là trung tuyến nên BN=12AC(2).
Từ (1) và (2) suy ra MI = BN.
Vậy BMNI là hình thang cân (hình thang có 2 đường chéo bằng nhau là hình thang cân).
Câu 9:
22/07/2024Cho tam giác ABC, các đường trung tuyến BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Đoạn thẳng DE song song và bằng với đoạn thẳng nào?
Xem đáp án
Đáp án đúng là: B
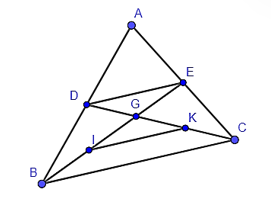
Trong tam giác ABC có D là trung điểm AB, E là trung điểm AC.
Do đó DE là đường trung bình của tam giác ABC.
Suy ra DE // BC và DE=12BC (tính chất đường trung bình của tam giác) (1).
Trong tam giác GBC có I là trung điểm GB, K là trung điểm GC.
Do đó IK là đường trung bình của tam giác GBC.
Suy ra IK // BC và IK=12BC (tính chất đường trung bình của tam giác) (2).
Từ (1) và (2) suy ra IK // DE và IK = DE.
Câu 10:
16/07/2024Cho tứ giác ABCD có AB = 2a, CD = 2b. Gọi E, F lần lượt là trung điểm của AD, BC. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: D
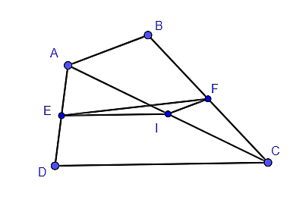
Gọi I là trung điểm của AC.
Trong tam giác ADC có E là trung điểm AD, I là trung điểm của AC.
Do đó EI là đường trung bình của tam giác ADC.
Suy ra EI=12CD hay EI=12⋅2b = b (tính chất đường trung bình của tam giác).
Trong tam giác ABC có F là trung điểm BC, I là trung điểm của AC.
Do đó FI là đường trung bình của tam giác ABC.
Suy ra FI=12AB hay FI=12⋅2a = a (tính chất đường trung bình của tam giác).
Trong tam giác EFI có: EF ≤ EI + FI (bất đẳng thức tam giác) hay EF ≤ b + a.