Câu hỏi:
19/07/2024 116
Cho tam giác OMN cân tại O. I là trung điểm của đường cao OH, NI cắt OM tại K. Từ H kẻ Hx song song với NK cắt OM tại D. Khi đó độ dài OM gấp mấy lần độ dài OK?
Cho tam giác OMN cân tại O. I là trung điểm của đường cao OH, NI cắt OM tại K. Từ H kẻ Hx song song với NK cắt OM tại D. Khi đó độ dài OM gấp mấy lần độ dài OK?
A. 2;
B. 4;
C. 3;
D. .
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
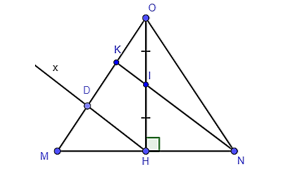
Vì tam giác OMN cân tại O nên OH vừa là đường cao vừa là đường trung tuyến.
Suy ra H là trung điểm của MN.
Trong tam giác MKN có H là trung điểm của MN, DH // KN, D ∈ MK.
Do đó D là trung điểm của MK.
Suy ra MD = DK (1).
Trong tam giác ODH có I là trung điểm của OH, KI // DH (do I ∈ NK), K ∈ OD.
Do đó K là trung điểm của OD.
Suy ra OK = DK (2).
Lại có OK + DK + MD = OM (3).
Từ (1), (2), (3) suy ra OM = 3OK.
Đáp án đúng là: C

Vì tam giác OMN cân tại O nên OH vừa là đường cao vừa là đường trung tuyến.
Suy ra H là trung điểm của MN.
Trong tam giác MKN có H là trung điểm của MN, DH // KN, D ∈ MK.
Do đó D là trung điểm của MK.
Suy ra MD = DK (1).
Trong tam giác ODH có I là trung điểm của OH, KI // DH (do I ∈ NK), K ∈ OD.
Do đó K là trung điểm của OD.
Suy ra OK = DK (2).
Lại có OK + DK + MD = OM (3).
Từ (1), (2), (3) suy ra OM = 3OK.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác MNP cân tại M có D là trung điểm của NP. Từ D kẻ DE song song với MP (E ∈ MN), kẻ DF song song với MN (F ∈ MP). Khi đó ME bằng với đoạn thẳng nào?
Cho tam giác MNP cân tại M có D là trung điểm của NP. Từ D kẻ DE song song với MP (E ∈ MN), kẻ DF song song với MN (F ∈ MP). Khi đó ME bằng với đoạn thẳng nào?
Câu 2:
Cho tam giác ABC, các đường trung tuyến BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Đoạn thẳng DE song song và bằng với đoạn thẳng nào?
Cho tam giác ABC, các đường trung tuyến BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Đoạn thẳng DE song song và bằng với đoạn thẳng nào?
Câu 3:
Cho tam giác ABC trên nửa mặt phẳng bờ AC không chứa điểm B lấy điểm D bất kì. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, AD, DC. Khi đó EF + FH + HG + GE bằng
Cho tam giác ABC trên nửa mặt phẳng bờ AC không chứa điểm B lấy điểm D bất kì. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, AD, DC. Khi đó EF + FH + HG + GE bằng
Câu 4:
Cho tam giác ABC vuông tại B, phân giác AD. Gọi M, N, I lần lượt là trung điểm của AD, AC, CD. Tứ giác BMNI là hình gì?
Cho tam giác ABC vuông tại B, phân giác AD. Gọi M, N, I lần lượt là trung điểm của AD, AC, CD. Tứ giác BMNI là hình gì?
Câu 5:
Cho tứ giác ABCD có AB = 2a, CD = 2b. Gọi E, F lần lượt là trung điểm của AD, BC. Khẳng định nào sau đây là đúng?
Cho tứ giác ABCD có AB = 2a, CD = 2b. Gọi E, F lần lượt là trung điểm của AD, BC. Khẳng định nào sau đây là đúng?
Câu 6:
Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AC. Qua A kẻ Ax song song với BC cắt HI tại K. Khi đó HK song song với:
Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AC. Qua A kẻ Ax song song với BC cắt HI tại K. Khi đó HK song song với:
Câu 7:
Cho tam giác MNP, trên MN lấy hai điểm D, E sao cho MD = DE = EN. Gọi I là trung điểm NP, PD cắt MI tại H. Khẳng định nào sau đây là đúng?
Cho tam giác MNP, trên MN lấy hai điểm D, E sao cho MD = DE = EN. Gọi I là trung điểm NP, PD cắt MI tại H. Khẳng định nào sau đây là đúng?
Câu 8:
Cho tam giác ABC đều, I là trung điểm BC. Từ I kẻ IK // AB (K ∈ AC), IH // AC (H ∈ AB). Tam giác IHK là tam giác gì?
Cho tam giác ABC đều, I là trung điểm BC. Từ I kẻ IK // AB (K ∈ AC), IH // AC (H ∈ AB). Tam giác IHK là tam giác gì?
Câu 9:
Cho tam giác ABC, AB = 4 cm, AC = 6 cm, BC = 8 cm. Kéo dài AB lấy điểm D sao cho AB = BD, kéo dài AC lấy điểm E sao cho AC = CE, kéo dài trung tuyến AM của tam giác ABC lấy F sao cho AM = MF. Khẳng định nào sau đây là đúng?
Cho tam giác ABC, AB = 4 cm, AC = 6 cm, BC = 8 cm. Kéo dài AB lấy điểm D sao cho AB = BD, kéo dài AC lấy điểm E sao cho AC = CE, kéo dài trung tuyến AM của tam giác ABC lấy F sao cho AM = MF. Khẳng định nào sau đây là đúng?











