Trắc nghiệm Phép chia số phức (có đáp án)
Trắc nghiệm Toán 12 Bài 3: Phép chia số phức
-
447 lượt thi
-
26 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
14/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có: z=21+i√3=2(1−i√3)(1+i√3)(1−i√3)
=2−2i√34=12−i√32
Suy ra ˉz=12+i√32
Câu 2:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
z=7−11i2−i=(7−11i)(2+i)22+12
=14+11+7i−22i5=25−15i5
=5−3i
⇒ˉz=5+3i
Vậy phần thực và phần ảo của ˉz là 5 và 3
Câu 3:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có: z=11+i=1−i(1+i)(1−i)
=1−i1−i2=1−i1+1=1−i2
=12−12i
⇒ˉz=12+12i
Câu 4:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Ta có 1z=ˉzz.ˉz=ˉz|z|2
Do đó 1−iz+i=(2−3i)ˉz|z|2+2
⇔1−iz+i=2−3iz+2
⇔−1+2iz=2−i
⇒z=−1+2i2−i=−4+3i5
Suy ra |z|=1
Câu 5:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có: z=5−3i, suy ra ˉz=5+3i
Do đó 1ˉz=15+3i=5−3i(5+3i)(5−3i)
=5−3i25−9i2=5−3i34=534−334i
⇒{a=534b=−334
⇒S=a+b=117
Câu 6:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Ta có ⇔z+1=1−i1+i
⇔z+1=−i
⇒z=−1−i
Suy ra w=z3+1
=(−1−i)3+1
=−(1+i)3+1=3−2i
⇒M(3;−2)
Câu 7:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Ta có:
|w|=9⇒|z2|=9⇔|z|2=9
⇔|z|=3⇔|m+3i1−i|=3
⇔|m+3i|√2=3
⇔|m+3i|=3√2
⇔√m2+9=3√2
⇔m2+9=18
⇔m2=9
⇔m=±3
Câu 8:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
z=a+bi
⇒z2=(a+bi)2
=a2+2abi+b2i2
=a2−b2+2abi
w=1(a+bi)2=1a2−b2+2abi
=a2−b2−2abi(a2−b2+2abi)(a2−b2−2abi)
=a2−b2−2abi(a2−b2)2−(2abi)2
=a2−b2−2abia4+b4−2a2b2−4a2b2i2
=a2−b2−2abia4+b4−2a2b2+4a2b2
=a2−b2−2abia4+b4+2a2b2
=a2−b2−2abi(a2+b2)2
=a2−b2(a2+b2)2−2ab(a2+b2)2i
Nên phần thực của số phức w là: a2−b2(a2+b2)2
Câu 9:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có:
3−4iz=(2+3i)ˉz|z|2+2+i
⇔3−4iz=(2+3i)ˉzz.ˉz+2+i
⇔3−4iz=2+3iz+2+i
⇔3−4i=2+3i+(2+i).z
⇔(2+i).z=1−7i
⇔z=1−7i2+i=−1−3i
Vậy |z|=√(−1)2+(−3)2=√10
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Giả thiết (1+2i)|z|=√10z−2+i
⇔|z|+2i.|z|+2−i=√10z
⇔|z|+2+(2|z|−1)i=√10z
Lấy môđun hai vế của (*), ta được
√(|z|+2)2+(2|z|−1)2=√10|z|
⇒|z|=1
Do đó: |z|4+|z|2=2
Câu 11:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Đặt z=x+yi(x;y∈ℝ) ta có: z−iz+i=x+yi−ix+yi+i=x+(y−1)ix+(y+1)i (ĐK z≠−i)
=[x+(y−1)i][x−(y+1)i]x2+(y+1)2
=x2−(y2−1)+[x(y−1)−x(y+1)]ix2+(y+1)2 là số thực khi phần ảo
xy−x−xy−xx2+(y+1)2=0⇔x=0
Do đó tập hợp điểm biểu diễn z là đường thẳng x=0 (trục tung) bỏ đi điểm (0;−1).
Câu 12:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có: |z−iz+i|=1
⇔|z−i|=|z+i| (với z≠−i)
Đặt z=x+yi(x;y∈ℝ) ta có:
|x+yi−i|=|x+yi+i|
⇔x2+(y−1)2=x2+(y+1)2
⇔y=0
Do đó tập hợp điểm biểu diễn z là đường thẳng (trục thực) bỏ đi điểm y=0
Câu 13:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có (2+3i)|z|=√26ˉz+3−2i
⇔2|z|−3+3i|z|+2i=√26z
⇔(2|z|−3)+(3|z|+2)i=√26z (*)
Lấy môđun 2 vế của biểu thức (*) ta được
√(2|z|−3)2+(3|z|+2)2=|√26z|
=√26|z| (*)
⇔13|z|2+13=26|z|2
⇔|z|4+|z|2−2=0
⇔[|z|2=1|z|2=−2
⇒|z|=1⇒|z|4+|z|2=2
Câu 14:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
(1+3i)z−5=7i
⇔z=7i+51+3i=135−45i
⇒ˉz=135+45i
Câu 15:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có: z=(1−i1+i)2016
=(−i)2016=(i4)504=1
Câu 16:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có: ˉz=24+7i⇒z=24−7i
Suy ra a+2b=10
Câu 17:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Gọi z=x+yi,x,y∈ℝ tìm được z=1−2i
Câu 18:
23/07/2024Cho số phức z thỏa mãn (1+i)z=3−i. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình bên?
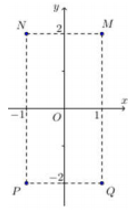
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
⇒z=3−i1+i=(3−i)(1−i)(1+i)(1−i)
=2−4i12+12=1−2i
⇒Q(1;−2) là điểm biểu diễn z.
Câu 19:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Đặt z=a+bi⇒ˉz=a−bi
Theo bài ra ta có:
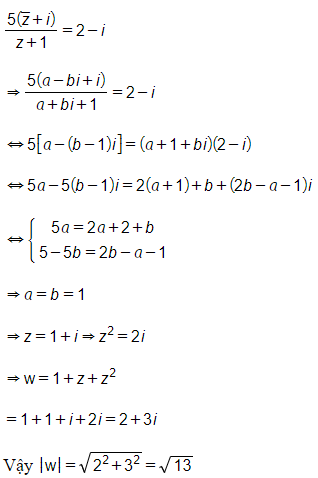
Câu 20:
22/07/2024Cho số phức z thỏa mãn (2−i)z=7−i. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình dưới
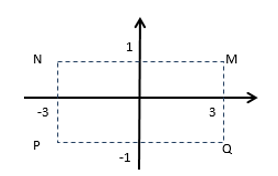
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
⇒z=7−i2−i=(7−i)(2+i)5
=15+5i5=3+i
Suy ra điểm có tọa độ (3; 1) sẽ biểu diễn số phức z, suy ra M thỏa mãn.
Câu 21:
14/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có:
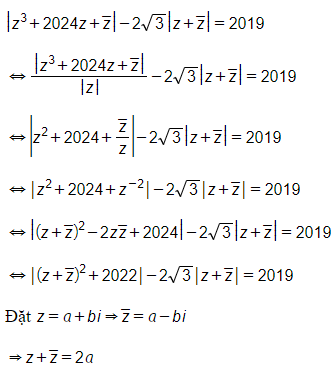
Khi đó phương trình cuối trở thành
|(2a)2+2022|−2√3.|2a|=2019
⇔4a2−4√3|a|+3=0
⇔(2|a|−√3)2=0
⇔|a|=√32⇔a=±√32
Mà |z|=1⇔|z|2=1
⇔a2+b2=1
⇒b2=1−a2=14
⇔b=±12
Vậy có bốn số phức thỏa mãn bài toán là:
z1=√32+12i,z2=√32−12i,
z3=−√32−12i,z4=−√32+12i,
Câu 22:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Đặt: z=x+yi. Theo giả thiết ta có: xy=625
Ta có:
z3+4i=x+yi3+4i=(x+yi)(3−4i)25
=3x+4y+(−4x+3y)i25
=3x+4y25+−4x+3y25i
Số phức z3+4i có phần thực là a=3x+4y25
⇒|a|=|3x+4y|25
Ta có: xy=625⇔y=625x
⇒|a|=|3x+4.625x|25
Vì 3x,625x cùng dấu nên
|3x+4.625x|≥2√3x.4.625x
=100.√3
Vậy |a|≥4√3.
Dấu bằng xảy ra ⇔3x=4.625x⇔x=±50√3
Câu 23:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Dễ dàng kiểm tra z = 0 không thỏa mãn (3−i)|z|=zw−1+1−i
Ta có: (3−i)|z|=zw−1+1−i
⇔zw−1=(3−i)|z|+i−1
⇔zw−1=(3|z|−1)+(1−|z|)i
⇒|zw−1|=√10|z|2−8|z|+2
⇒|w−1|=√|z|210|z|2−8|z|+2
Nhận xét
T=|w+i|≤|w−1|+|1+i|
=1√2|z|2−8|z|+10+√2
=1√2(1|z|−2)2+2+√2≤3√22
Dấu bằng xảy ra khi và chỉ khi:
{|z|=12w−1=k(1+i)(3−i)|z|=zw−1+1−i(k>0)
⇔{|z|=12w−1=k(1+i)(3−i)12=zk(1+i)+1−i(k>0)
⇔{|z|=12w−1=k(1+i)z=1+i2.2k1−i
⇔{|z|=12w−1=k(1+i)|z|=k(do k>0)
⇔{|z|=12w−1=12(1+i)z=1+i2.2k1−i
⇔{z=i2w=32+12i
Vậy MaxT=3√22
Câu 24:
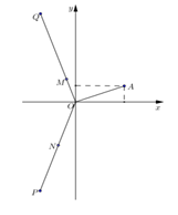
23/07/2024Cho số phức z thỏa mãn |z|=√22 và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức w=1iz là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Do điểm A là điểm biểu diễn của z nằm trong góc phần tư thứ nhất của mặt phẳng Oxy nên gọi z=a+bi(a,b>0)
Do |z|=√22⇒√a2+b2=√22
Lại có: w=1iz=−ba2+b2−aa2+b2i
|w|=|1iz|=1|i|.|z|
=√2=2|z|=2OA
Vậy điểm biểu diễn của số phức w là điểm P.
Câu 25:
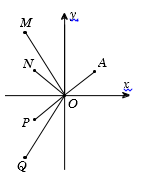
18/07/2024Cho số phức z thỏa mãn |z|=1 và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức w=1iz là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Gọi z=x+yi(x;y∈R).
Từ giả thiết ta có {x2+y2=1x>0,y>0
Ta có: w=1iz=−iz=−ix+yi
=−i(x−yi)(x+yi)(x−yi)
=−y+xix2+y2=−y−xi
Vì x > 0, y > 0 nên điểm biểu diễn số phức w có tọa độ là (−y;−x) (đều có hoành độ và tung độ âm).
Đồng thời w=√(−y)2+(−x)2=1=|z|
Suy ra, điểm biểu diễn của số phức w nằm trong góc phần tư thứ III và cách gốc tọa độ O một khoảng bằng OA.
Quan sát hình vẽ ta thấy có điểm P thỏa mãn.
Câu 26:
14/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
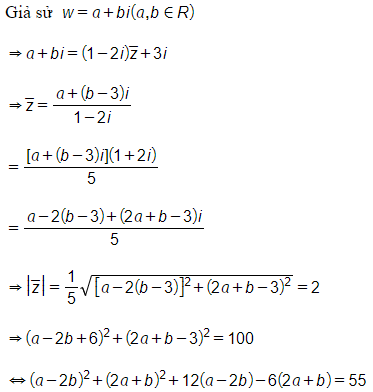
Hay tập hợp điểm biểu diễn số phức w=(1−2i)ˉz+3i là đường tròn x2+(y−3)2=20
Có thể bạn quan tâm
- Trắc nghiệm Phép chia số phức (có đáp án) (446 lượt thi)
- 11 câu trắc nghiệm: Phép chia số phức có đáp án (324 lượt thi)
- Trắc nghiệm Phép chia số phức có đáp án (Thông hiểu) - Phần 1 (353 lượt thi)
- Trắc nghiệm Phép chia số phức có đáp án (Nhận biết) (327 lượt thi)
- Trắc nghiệm Phép chia số phức có đáp án (Vận dụng) (302 lượt thi)
- Trắc nghiệm Phép chia số phức có đáp án (340 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Cộng, trừ và nhân số phức (có đáp án) (634 lượt thi)
- Trắc nghiệm Số phức (có đáp án) (504 lượt thi)
- Trắc nghiệm Phương trình bậc hai với hệ số thực (có đáp án) (471 lượt thi)
- 46 câu trắc nghiệm Ôn tập Giải tích 12 có đáp án (407 lượt thi)
- Trắc nghiệm Số phức có đáp án (387 lượt thi)
- Trắc nghiệm Số phức có đáp án (Thông hiểu) (384 lượt thi)
- 12 câu trắc nghiệm: Phương trình bậc hai với hệ số thực có đáp án (382 lượt thi)
- Trắc nghiệm Cộng, trừ và nhân số phức có đáp án (Phần 1) (376 lượt thi)
- Trắc nghiệm Số phức có đáp án (Nhận biết) (374 lượt thi)
- Trắc nghiệm Số phức có đáp án (Vận dụng) (368 lượt thi)
