25 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 12 Bài 2: Cộng, trừ và nhân số phức

\bar{z} = \frac{1}{3} [{(\bar{1 - 2 i})}^{2} - z]

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Ta có $z = x + y i (x, y \in ℝ)$

$\Rightarrow x - y i = \frac{1}{3} [{(1 + 2 i)}^{2} - (x + y i)]$

$\Leftrightarrow 3 (x - y i) = - 3 + 4 i - x - y i$

$= - 3 - x + (4 - y) i$

$\Leftrightarrow {\begin{cases} 3 x = - 3 - x \\ - 3 y = 4 - y \end{cases}$

$\Leftrightarrow {\begin{cases} x = - \frac{3}{4} \\ y = - 2 \end{cases}$

Câu 2:

Rút gọn biểu thức

P = {(1 - i)}^{2016}

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

$P = {[{(1 - i)}^{2}]}^{1008} = {(- 2 i)}^{1008}$

$= 2^{2008} {(i^{2})}^{504} = 2^{2008}$

Câu 3:

z = a + b i, (a, b \in ℝ)

z = {(\frac{1 - i}{1 + i})}^{2016}

. Tính tổng

S = a + b

A. -1

B. 0

C. 1

D. 2

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Ta có: $z = {(- i)}^{1008} = {(i^{2})}^{504} = 1$

Câu 4:

z = a + b i, (a, b \in ℝ)

\bar{z} = \frac{{(1 - 2 i)}^{5}}{2 + i}

. Tính tổng

S = a + 2 b

A. 38.

B. 10.

C. 31.

D. 55.

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

$\bar{z} = (- 4 + 3 i) {(1 - 2 i)}^{2}$

$= 24 + 7 i$

$\Rightarrow z = 24 - 7 i$

Câu 5:

.Tìm phần thực a của số phức z

z = 1 + z + {(1 + z)}^{2} + {(1 + i)}^{3} + ... + {(1 + i)}^{20}

A. z=1025−1025i

B. z=−1025−1025i

C. z=−1025+1025i

D. z=1025+1025i

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

$z = (1 + i) . \frac{{(1 + i)}^{20} - 1}{(1 + i) - 1}$

$= (1 + i) . \frac{{(2 i)}^{10} - 1}{i}$

$= (1 + i) . \frac{2^{10} . {(i^{2})}^{5} - 1}{i}$

$= - 1025 + 1025 i$

Câu 6:

. Tìm phần thực a của số phức z.

z = {(1 + z)}^{2} + {(1 + i)}^{3} + ... + {(1 + i)}^{22}

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Ta có: $z = (1 + i) . [(1 + i) . \frac{{(1 + i)}^{21} - 1}{(1 + i) - 1}]$

$= 2 [{(2 i)}^{10} (1 + i) - 1]$

$= 2 [2^{10} . {(i^{2})}^{5} (1 + i) - 1]$

$= 2 (- 1 - 2^{10} - 2^{10} . i)$

Câu 7:

Tìm phần thực a và phần ảo b của số phức

z=1+i+i2+i3+...+i2016

A. a=0, b=−1

B. a=0, b=1

C. a=1, b=1

D. a=1, b=0

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

$z = 1 + i . \frac{i^{2016} - 1}{i - 1}$

$= 1 + i . \frac{{(i^{2})}^{1008} - 1}{i - 1}$

Câu 8:

Tìm môđun của số phức

z = 1 + i^{2} + i^{4} + ... + i^{2 n} + ... + i^{2016},

n \in ℕ

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

$z = 1 + i^{2} . \frac{{(i^{2})}^{1008} - 1}{i^{2} - 1} = 1$

$\Rightarrow | z | = 1$

Câu 9:

. Trong mặt phẳng phức, tập hợp các điểm biểu diễn số phức

Cho số phức z thỏa mãn

|z - i| = |z - 1 + 2 i|

w = (2 - i) z + 1

là một đường thẳng. Viết phương trình đường thẳng đó.

A. x−7y−9=0

B. x+7y−9=0

C. x+7y+9=0

D. x−7y+9=0

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Ta có: $w = (2 - i) z + 1 \Leftrightarrow z = \frac{w - 1}{2 - i}$

Suy ra $|z - i| = |z - 1 + 2 i|$

$\Leftrightarrow | \frac{w - 1}{2 - i} - i | = | \frac{w - 1}{2 - i} - 1 + 2 i |$

$\Leftrightarrow |\frac{w - 1 - 2 i + i^{2}}{2 - i}| = |\frac{w - 1 - (1 - 2 i) (2 - i)}{2 - i}|$

$\Leftrightarrow |w - 2 - 2 i| = |w - 1 + 5 i|$

Đặt $w = x + y i (x; y \in ℝ)$ ta có:

$|w - 2 - 2 i| = |w - 1 + 5 i|$

$\Leftrightarrow {(x - 2)}^{2} + {(y - 2)}^{2} = {(x - 1)}^{2} + {(y + 5)}^{2}$

$\Leftrightarrow 2 x + 14 y + 18 = 0$

$\Leftrightarrow x + 7 y + 9 = 0$

Do đó tập hợp điểm biểu diễn w là đường thẳng $x + 7 y + 9 = 0$

Câu 10:

. Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện

v = a + b i

|z - v| = 1

A. Đường thẳng (x−a)+(y−b)=1

B. Đường thẳng y=b

C. Đường tròn ${(x - a)}^{2} + {(y - b)}^{2} = 1$

D. Đường thẳng x=a

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện $|z - v| = 1$ là đường tròn tâm $I (v) = I (a; b)$ bán kính $R = 1$ .

Câu 11:

Tìm phần thực a của số phức

z = 1 + 1 + i + {(1 + i)}^{2} + {(1 + i)}^{3} + . . . + {(1 + i)}^{26}

A. $- 2^{13}$

B. $a = 2^{13}$

C. $- 1 - 2^{13}$

D. $1 + 2^{13}$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

$z = 1 + (1 + i) . \frac{{(1 + i)}^{26} - 1}{(1 + i) - 1}$

$= 1 + (1 + i) . \frac{{(2 i)}^{13} - 1}{i}$

$= 1 + (1 + i) . \frac{2^{13} . {(i^{2})}^{6} i - 1}{i}$

$= 8192 + 8193 i$

Câu 12:

Tính môđun của số phức z thỏa mãn

z . \bar{z} + 3 (z - \bar{z}) = 4 - 3 i

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

$a^{2} + b^{2} + 3.2 b i = 4 - 3 i$

$\Leftrightarrow {\begin{cases} 6 b = - 3 \\ a^{2} + b^{2} = 4 \end{cases}$

$\Leftrightarrow | z | = \sqrt{a^{2} + b^{2}} = 2$

Câu 13:

Cho số phức z thỏa $(1 + 3 i) z + 2 i = - 4$ . Điểm nào sau đây biểu diễn cho z trong các điểm M, N, P, Q ở hình bên?

A. Điểm M

B. Điểm N

C. Điểm P

D. Điểm Q

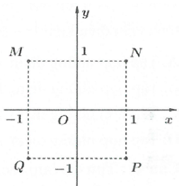
Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Ta có $(1 + 3 i) z + 2 i = - 4$

$\Leftrightarrow z = \frac{- 4 - 2 i}{1 + 3 i} \Leftrightarrow z = - 1 + i$

$\Rightarrow (- 1; 1)$ là điểm biểu diễn.

Câu 14:

có điểm biểu diễn là điểm nào trong các điểm M, N, P, Q ở hình vẽ?

Cho số phức z thỏa

z - (2 + 3 i) \bar{z} = 1 - 9 i

. Số phức

w = 5. {(i z)}^{- 1}

Trắc nghiệm Cộng, trừ và nhân số phức có đáp án - Toán lớp 12 (ảnh 4)

A. Điểm N

B. Điểm Q

C. Điểm M

D. Điểm P

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Giả sử $z = x + y i \Rightarrow \bar{z} = x - y i$

Ta có $z - (2 + 3 i) \bar{z} = 1 - 9 i$

$\Leftrightarrow (x + y i) - (2 + 3 i) (x - y i) = 1 - 9 i$

$\Leftrightarrow x + y i - 2 x - 3 y - 3 x i + 2 y i = 1 - 9 i$

$\Leftrightarrow (- x - 3 y) + (- 3 x + 3 y) i = 1 - 9 i$

$\Leftrightarrow \{\begin{cases} - x - 3 y = 1 \\ - 3 x + 3 y = - 9 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = 2 \\ y = - 1 \end{cases}$

Do đó $z = 2 - i$

$\Rightarrow w = 5. {(i z)}^{- 1} = \frac{5}{i z}$

$= \frac{5}{i (2 - i)} = \frac{5}{1 + 2 i} = 1 - 2 i$

$\Rightarrow (1; - 2)$ là điểm biểu diễn.

Câu 15:

Cho số phức z thỏa mãn $3 z + 2 z = {(4 - i)}^{2}$ . Tính môđun của số phức z.

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

$3 (a + b i) + 2 (a - b i) = 15 - 8 i$

$\Leftrightarrow {\begin{cases} 3 a + 2 a = 15 \\ 3 b - 2 b = - 8 \end{cases}$

$\Leftrightarrow a = 3; b = - 8$

$\Rightarrow | z | = \sqrt{73}$

Câu 16:

. Hãy tìm môđun của số phức z

Cho số phức z thỏa mãn

2 z = i (\bar{z} + 3)

Xem đáp án

Đáp án đúng: A

*Lời giải

$2 (a + b i) = i (a + 3 - b i)$

$\Leftrightarrow {\begin{cases} 2 a = b \\ 2 b = a + 3 \end{cases}$

$\Leftrightarrow a = 1; b = 2$

$\Rightarrow | z | = \sqrt{5}$

*Phương pháp giải

- áp dụng các phép tính của số phức để biến đổi và tính

- ta có số phức z = a + bi. Thay vào đề bài và biến đổi để tìm ra a và b cho số phức z

*Lý thuyến cần nắm về cộng - trừ - nhân số phức:

1. Phép cộng và phép trừ

– Phép cộng và phép trừ hai số phức được thực hiện theo quy tắc cộng, trừ đa thức.

– Tổng quát:

(a + bi) + (c + di) = (a + c) + (b + d).i

(a + bi) – (c + di) = (a – c) + (b – d).i

2. Phép nhân

– Phép nhân hai số phức được thực hiện theo quy tắc nhân hai đa thức, rồi thay i2 = – 1 vào kết quả.

– Tổng quát:

(a + bi).(c + di) = ac + adi + bci + bdi2 = ac + adi + bci – bd

Vậy (a + bi). (c + di) = (ac – bd) + (ad + bc).i

– Chú ý: Phép cộng và phép nhân số phức có tất cả các tính chất của phép cộng và phép nhân các số thực (giao hoán, kết hợp, cộng với 0, nhân với 1, tính chất phân phối,…).

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Cộng, trừ và nhân số phức (mới 2024 + Bài Tập) – Toán 12

50 Bài tập Cộng, trừ và nhân số phức Toán 12 mới nhất

Câu 17:

z = a + b i (a, b \in ℝ)

z i + 2 \bar{z} = 4 - 4 i

. Tìm

2^{a} + 2^{b}

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

$(a + b i) + 2 (a - b i) = 4 - 4 i$

$\Leftrightarrow {\begin{cases} - b + 2 a = 4 \\ a - 2 b = - 4 \end{cases}$

$\Leftrightarrow a = b = 4$

Câu 18:

Tìm điểm biểu diễn của số phức z thỏa mãn

z = i {(1 + 2 i)}^{2}

A. $M_{1} (- 4; - 3)$

B. $M_{2} (4; - 3)$

C. $M_{3} (- 4; 3)$

D. $M_{4} (4; 3)$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

$z = i {(1 + 2 i)}^{2} = i (- 3 + 4 i) = - 4 - 3 i$

$\Rightarrow (- 4; - 3)$ là điểm biểu diễn.

Câu 19:

Tìm điểm biểu diễn của số phức z thỏa mãn

(9 + 5 i) z + (7 - 2 i) = 0

A. M(1;2)

B. N(1;1)

C. P(2;2)

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

$(9 + 5 i) z + (7 - 2 i) = 0$

$\Leftrightarrow z = \frac{2 i - 7}{9 + 5 i}$

$\Leftrightarrow z = - \frac{1}{2} + \frac{1}{2} i$

$\Rightarrow (- \frac{1}{2}; \frac{1}{2})$ là điểm biểu diễn.

Câu 20:

Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện là một số thuần ảo

v = (z - i) (2 + i)

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Đặt $z = x + y i (x; y \in ℝ)$ ta có: $v = (z - i) (2 + i)$

$= (x + y i - i) (2 + i)$

Số phức $v = (z - i) (2 + i)$ là một số thuần ảo khi phần thực $2 x - (y - 1) = 0$ hay $2 x - y + 1 = 0$ .

Do đó tập hợp điểm biểu diễn số phức z là đường thẳng $2 x - y + 1 = 0$

Câu 21:

Trên mặt phẳng tọa độ , tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện số phức

w = z (2 + 3 i) + 5 - i

là số thuần ảo

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

Đặt $z = x + y i (x; y \in ℝ)$ ta có: $w = z (2 + 3 i) + 5 - i$

$= (x + y i) (2 + 3 i) + 5 - i$

$= 2 x + 2 y i + 3 x i - 3 y + 5 - i$

$= (2 x - 3 y + 5) + (3 x + 2 y - 1) i$

Số phức $w = z (2 + 3 i) + 5 - i$ là số thuần ảo khi phần thực $2 x - 3 y + 5 = 0$

Do đó tập hợp điểm biểu diễn số phức z là đường thẳng $2 x - 3 y + 5 = 0$ .

Câu 22:

Tìm tất cả các số phức z thỏa mãn

|z - 2 i| = \sqrt{5}

và điểm biểu diễn của z thuộc đường thẳng

d : 3 x - y + 1 = 0

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

Đặt $z = x + y i (x; y \in ℝ)$ ta có: $|z - 2 i| = \sqrt{5}$

$\Leftrightarrow x^{2} + {(y - 2)}^{2} = 5$

Giải hệ phương trình $\{\begin{cases} x^{2} + {(y - 2)}^{2} = 5 \\ 3 x - y + 1 = 0 \end{cases}$

$\Leftrightarrow {\begin{cases} x^{2} + {(y - 2)}^{2} = 5 \\ y = 3 x + 1 \end{cases}$

$\Leftrightarrow {\begin{cases} x^{2} + {(3 x + 1 - 2)}^{2} = 5 \\ y = 3 x + 1 \end{cases}$

$\Leftrightarrow \{\begin{cases} 10 x^{2} - 6 x - 4 = 0 \\ y = 3 x + 1 \end{cases}$

$\Leftrightarrow {\begin{cases} x = 1 \Rightarrow y = 4 \\ x = \frac{- 2}{5} \Rightarrow y = - \frac{1}{5} \end{cases}$

Do đó $z = 1 + 4 i$ và $z = \frac{- 2}{5} - \frac{1}{5} i$ là các số phức cần tìm.

Câu 23:

Tập hợp các điểm M biểu diễn số phức z sao cho

z^{2} = {(\bar{z})}^{2}

là

A. Gốc tọa độ

B. Trục hoành

C. Trục tung

D. Trục tung và trục hoành

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

Đặt $z = x + y i (x; y \in ℝ) \Rightarrow \bar{z} = x - y i$

ta có: $z^{2} = {(\bar{z})}^{2} \Leftrightarrow {(x + y i)}^{2} = {(x - y i)}^{2}$

Do đó tập hợp điểm biểu diễn số phức z là trục hoành và trục tung.

Câu 24:

Cho hai số phức

z_{1}, z_{2}

|z_{1}| = |z_{2}| = 1

và

|z_{1} + z_{2}| = \sqrt{3}

. Tính

|z_{1} - z_{2}|

A. 1.

B. 2.

C. 3.

D. 4.

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Ta có ${|z_{1} + z_{2}|}^{2} + {|z_{1} - z_{2}|}^{2} = 2 ({|z_{1}|}^{2} + {|z_{2}|}^{2})$

$\Rightarrow | z_{1} - z_{2} | = 1$

Câu 25:

Cho hai số phức

z_{1}, z_{2}