Câu hỏi:
19/07/2024 1,918
Cho số phức z=a+bi(ab≠0). Tìm phần thực của số phức w=1z2
![]()
![]()
![]()
![]()
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: D
Giải thích:
Lời giải:
z=a+bi
⇒z2=(a+bi)2
=a2+2abi+b2i2
=a2−b2+2abi
w=1(a+bi)2=1a2−b2+2abi
=a2−b2−2abi(a2−b2+2abi)(a2−b2−2abi)
=a2−b2−2abi(a2−b2)2−(2abi)2
=a2−b2−2abia4+b4−2a2b2−4a2b2i2
=a2−b2−2abia4+b4−2a2b2+4a2b2
=a2−b2−2abia4+b4+2a2b2
=a2−b2−2abi(a2+b2)2
=a2−b2(a2+b2)2−2ab(a2+b2)2i
Nên phần thực của số phức w là: a2−b2(a2+b2)2
Đáp án: D
Giải thích:
Lời giải:
z=a+bi
⇒z2=(a+bi)2
=a2+2abi+b2i2
=a2−b2+2abi
w=1(a+bi)2=1a2−b2+2abi
=a2−b2−2abi(a2−b2+2abi)(a2−b2−2abi)
=a2−b2−2abi(a2−b2)2−(2abi)2
=a2−b2−2abia4+b4−2a2b2−4a2b2i2
=a2−b2−2abia4+b4−2a2b2+4a2b2
=a2−b2−2abia4+b4+2a2b2
=a2−b2−2abi(a2+b2)2
=a2−b2(a2+b2)2−2ab(a2+b2)2i
Nên phần thực của số phức w là: a2−b2(a2+b2)2
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Có bao nhiêu số phức z thỏa mãn |z|=1 và |z3+2024z+ˉz|−2√3|z+ˉz|=2019?
Câu 2:
Cho số phức z thỏa mãn z+2(2−i)3ˉz1+i+(4+i)5=422+1088i. Khẳng định nào sau đây là khẳng định đúng?
Câu 3:
Cho số phức z thỏa z=(1−i1+i)2016. Viết z dưới dạng z=a+bi,a,b∈ℝ. Khi đó tổng a+b có giá trị bằng bao nhiêu?
Câu 4:
Cho số phức z≠0 thỏa mãn 1−iz+i=(2−3i)ˉz|z|2+2. Hỏi mệnh đề nào đúng?
Câu 5:
Cho số phức z thỏa ˉz=(1−2i)52+i. Viết z dưới dạng z=a+bi,a,b∈ℝ . Khi đó tổng a+2b có giá trị bằng bao nhiêu?
Câu 6:
Cho số phức z có tích phần thực và phần ảo bằng 625. Gọi a là phần thực của số phức z3+4i. Giá trị nhỏ nhất của |a| bằng:
Câu 7:
Cho số phức z thay đổi, luôn có |z|=2. Khi đó tập hợp điểm biểu diễn số phức w=(1−2i)ˉz+3i là:
Câu 8:
Cho số phức z=m+3i1−i,m∈R. Số phức w=z2 có |w|=9. Khi các giá trị của m là
Câu 9:
Xác định tập hợp các điểm biểu diễn số phức z thỏa mãn z−iz+i là số thực
Câu 10:
Cho số phức z thỏa mãn |z|=√22 và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức w=1iz là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là:
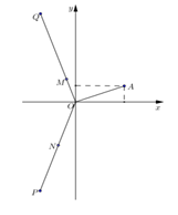
Cho số phức z thỏa mãn |z|=√22 và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức w=1iz là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là:

Câu 11:
Cho số phức z thỏa mãn |z−iz+i|=1. Tìm tập hợp các điểm biểu diễn số phức z trong mặt phẳng phức
Câu 12:
Cho các số phức z và w thỏa mãn (3−i)|z|=zw−1+1−i. Tìm GTLN của T=|w+i|
Câu 13:
Cho số phức z thỏa mãn (1+i)z=3−i. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình bên?
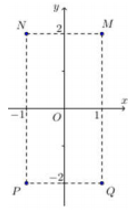
Cho số phức z thỏa mãn (1+i)z=3−i. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình bên?

Câu 14:
Cho số phức z thỏa mãn (2−i)z=7−i. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình dưới
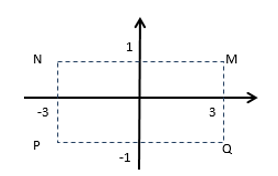
Cho số phức z thỏa mãn (2−i)z=7−i. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình dưới



