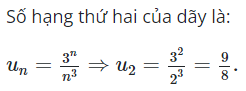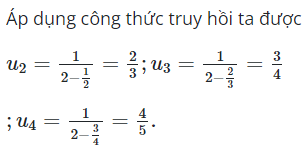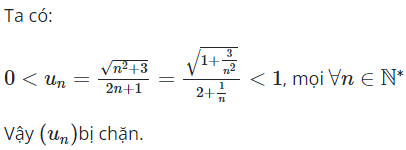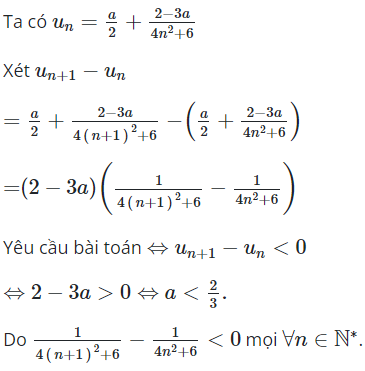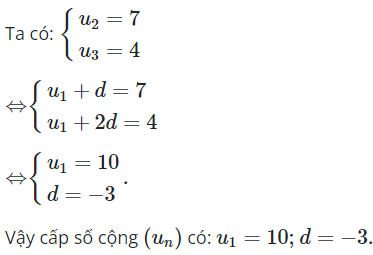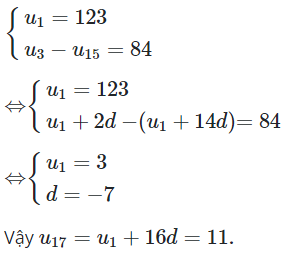Trắc nghiệm Toán 11 Ôn tập chương 3
-
1169 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
21/07/2024Cho cấp số nhân có 5 số hạng đầu là 1;4;16;64;256. Khi đó tổng của số hạng đầu của cấp số nhân đó bằng
 Xem đáp án
Xem đáp án
Chọn C.
Nhận xét: 1;4;16;64;256 là cấp số công có ![]()
Áp dụng công thức cấp số nhân ta được: 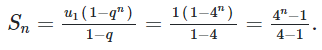
Câu 2:
23/07/2024Cho cấp số nhân (un) thỏa mãn {u2+u4=10u1+u3+u5=-21. Tìm số hạng đầu và công bội
 Xem đáp án
Xem đáp án
Chọn B.
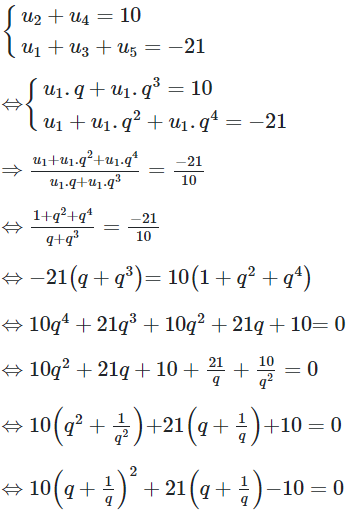
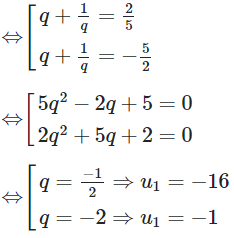
Câu 3:
23/07/2024Một tứ giác lồi có số đo các góc lập thành một cấp số nhân. Biết rằng số đo của góc nhỏ nhất bằng 19 số đo của góc nhỏ thứ ba. Số đo của các góc trong tứ giác đó lần lượt là
 Xem đáp án
Xem đáp án
Chọn B.
Gọi lần lượt là số đo bốn góc cần tìm.
vì lập thành 1 cấp số nhân nên ![]()
Theo đề ta có:
Vậy ta có hệ phương trình:
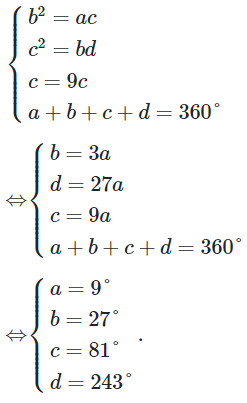
Câu 4:
22/07/2024Cho dãy số xác định bởi . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn C.
Nhận xét:
![]() là cấp số cộng với công sai 0; là cấp số nhân với công bội 1.
là cấp số cộng với công sai 0; là cấp số nhân với công bội 1.
Câu 5:
12/12/2024Cho cấp số cộng có tổng n số hạng đầu là . Giá trị của số hạng thứ 10 của cấp số cộng là
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Lời giải
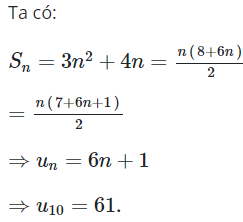
*Phương pháp giải:
Tổng n số hạng đầu tiên Sn được xác định bởi công thức:
*Lý thuyết:
1) Cấp số cộng là gì?
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
- Số không đổi d được gọi là công sai của cấp số cộng.
- Nếu (un) là một cấp số cộng với công sai d, ta có công thức truy hồi
Nhận xét:
- Cấp số cộng (un) là một dãy số tăng khi và chỉ khi công sai d > 0.
- Cấp số cộng (un) là một dãy số giảm khi và chỉ khi công sai d < 0.
- Đặc biệt, khi d = 0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều bằng nhau).
2) Số hạng tổng quát của cấp số cộng (un) được xác định bởi công thức:
un = u1 + (n - 1)d với .
3) Tính chất của cấp số cộng
Ba số hạng là ba số hạng liên tiếp của cấp số cộng khi và chỉ khi .
4) Tổng n số hạng đầu tiên Sn được xác định bởi công thức:
Xem thêm
Câu 6:
19/07/2024Cho ba số lập thành cấp số cộng và ba số lập thành cấp số nhân thì bằng
 Xem đáp án
Xem đáp án
Chọn C.
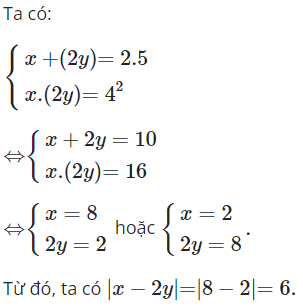
Câu 7:
23/07/2024Cho ba số theo thứ tự lập thành cấp số cộng và ba số theo thứ tự lập thành cấp số nhân thì bằng?
 Xem đáp án
Xem đáp án
Chọn A.
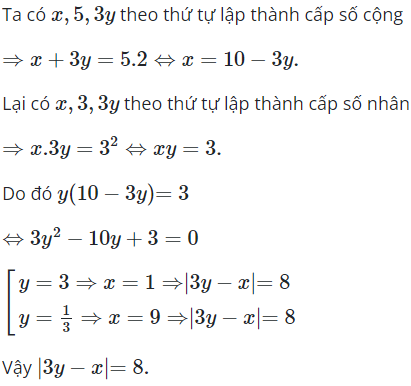
Câu 8:
23/07/2024Cho cấp số nhân . Dãy số nào dưới đây không phải là cấp số nhân?
 Xem đáp án
Xem đáp án
Chọn B.
Giả sử cấp số nhân có công bội là q.
Trường hợp thì cả 4 dãy đều là cấp số nhân.
Trường hợp thì cả 4 dãy đều là cấp số nhân.
Trường hợp: và ta có:
* Dãy số ![]() có
có ![]() nên dãy số này là cấp số nhân có công bội là
nên dãy số này là cấp số nhân có công bội là
* Dãy số ![]() có
có
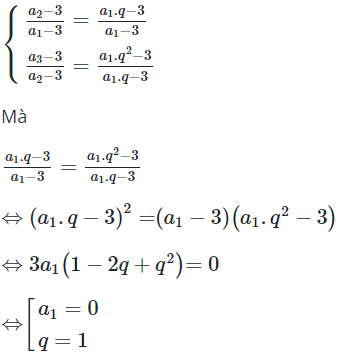
nên dãy số ![]() không là cấp số nhân trong trường hợp
không là cấp số nhân trong trường hợp ![]()
* Dãy số ![]() có
có ![]() nên dãy số này là cấp số nhân có công bội là q.
nên dãy số này là cấp số nhân có công bội là q.
* Dãy số ![]() có
có 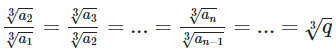 nên dãy số này là cấp số nhân có công bội là
nên dãy số này là cấp số nhân có công bội là
Câu 9:
19/07/2024Gọi S là tập hợp tất cả các giá trị của tham số m để phương trình có 4 nghiệm phân biệt lập thành cấp số cộng. Tổng giá trị của các phần tử thuộc S là
 Xem đáp án
Xem đáp án
Chọn D.
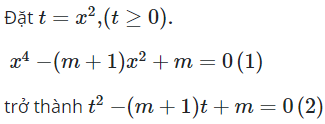
Để (1) có 4 nghiệm phân biệt lập thành cấp số cộng thì (2) phải có hai nghiệm thỏa:
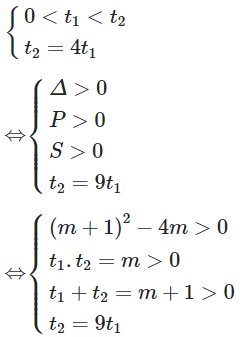
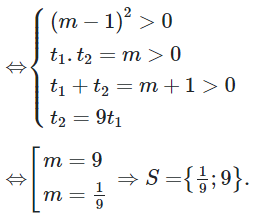
Vậy tổng giá trị của các phần tử thuộc S là ![]()
Câu 10:
22/07/2024Cho dãy số xác định bởi . Tìm chữ số hàng đơn vị của ?
 Xem đáp án
Xem đáp án
Chọn D.
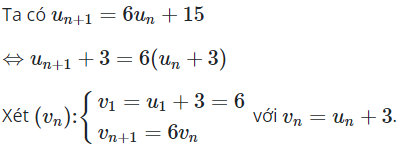
Suy ra là cấp số nhân với , công bội và
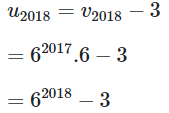
Vì chữ số tận cùng của là 6 nên chữ số tận cùng của là 3
Câu 11:
23/07/2024Một hãng taxi áp dụng mức giá đối với khách hàng theo hình thức bậc thang như sau: Mỗi bậc áp dụng cho 10 km. Bậc 1 (áp dụng cho 10km đầu) có giá trị 10.000đ/1km, giá mỗi km ở các bậc tiếp theo giảm 5% so với giá của bậc trước đó. Bạn An thuê hãng taxi đó để đi quãng đường 114km, nhưng khi đi được 50km thì bạn Bình đi chung hết quãng đường còn lại. Tính số tiền mà bạn An phải trả, biết rằng mức giá áp dụng từ lúc xe xuất phát và số tiền trên quãng đường đi chung bạn An chỉ phải trả 20% (Kết quả làm trong đến hàng nghìn).
 Xem đáp án
Xem đáp án
Chọn C.

Số tiền bạn An phải trả cho quãng đường chung là

Câu 12:
08/10/2024Dãy số nào sau đây là một cấp số nhân?
 Xem đáp án
Xem đáp án
Phương pháp:
+ Áp dụng công thức cấp số nhân:
Cách 1: Số hạng tổng quát của cấp số nhân (un) được xác định bởi công thức:
un = u1 . qn - 1 với ∀n ∈ N*, n ≥ 2
Cách 2: Lập tỷ lệ: thì dãy số đã cho là một cấp số nhân với công bội q.
Chọn B.
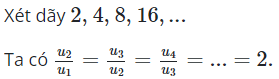
Vậy dãy số là một cấp số nhân với và công bội
Xem thêm các bài viết tương tự chi tiết, hay: 15 Bài tập Cấp số nhân có lời giải
Câu 13:
09/11/2024Dãy số cho bởi: . Số hạng thứ 3 của dãy là
 Xem đáp án
Xem đáp án
Đáp án đúng là D.
Lời giải
Ta có dãy cho bởi 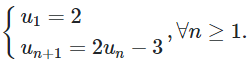
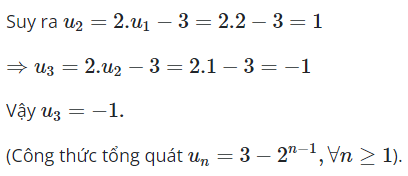
*Phương pháp giải:
Sử dụng công thức truy hồi cảu cấp số cộng
*Lý thuyết :
- Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ sai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Số d được gọi là công sai của cấp số cộng.
- Nếu (un) là cấp số cộng với công sai d, ta có công thức truy hồi:
un+1 = un + d với (1)
- Đặc biệt, khi d = 0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều bằng nhau).
Xem thêm
Lý thuyết Cấp số cộng (mới + Bài Tập) – Toán 11
TOP 40 câu Trắc nghiệm Cấp số cộng (có đáp án ) – Toán 11
Câu 15:
20/07/2024Cho dãy số . Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn B.
Ta có dãy số không tăng không giảm và không bị chặn.
Câu 16:
22/07/2024Cho cấp số nhân có . Khi đó số hạng thứ 3 của cấp số nhân là
 Xem đáp án
Xem đáp án
Chọn D.
Số hạng thứ ba của cấp số nhân là
Câu 17:
16/11/2024Cho cấp số cộng , biết và . Tính công sai của cấp số cộng đã cho.
 Xem đáp án
Xem đáp án
Đáp án đúng là B.
Lời giải
Ta có là cấp số cộng nên ![]()
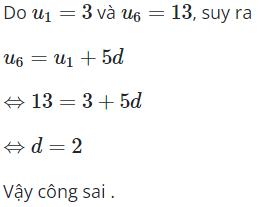
*Phương pháp giải:
Sử dụng công thức số hạng tổng quát![]()
*Lý thuyết:
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ sai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Số d được gọi là công sai của cấp số cộng.
- Nếu (un) là cấp số cộng với công sai d, ta có công thức truy hồi:
un+1 = un + d với (1)
- Đặc biệt, khi d = 0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều bằng nhau).
- Ví dụ 1. Dãy số hữu hạn: 1, 4, 7, 10, 13, 16, 19 là một cấp số cộng với số hạng đầu u1 = 1; công sai d = 3.
II. Số hạng tổng quát
- Định lí: Nếu cấp số cộng (un) có số hạng đầu u1 và công sai d thì số hạng tổng quát un được xác định bởi công thức:
un = u1 + (n – 1)d với n ≥ 2.
Xem thêm
Câu 18:
22/07/2024Cho cấp số nhân lùi vô hạn có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức nào sau đây
 Xem đáp án
Xem đáp án
Chọn B.
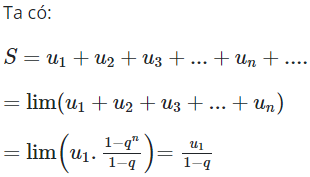
Câu 21:
23/07/2024Cho dãy số có công thức tổng quát là thì số hạng thứ n + 3 là?
 Xem đáp án
Xem đáp án
Chọn B.
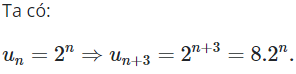
Câu 22:
23/07/2024Cho cấp số nhân có . Tính tổng của 23 số hạng đầu tiên của cấp số cộng trên.
 Xem đáp án
Xem đáp án
Chọn A.
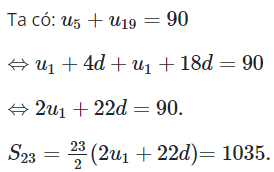
Câu 26:
22/07/2024Xét dãy các số tự nhiên chẵn liên tiếp Số 2018 là số hạng thứ mấy?
 Xem đáp án
Xem đáp án
Chọn C.
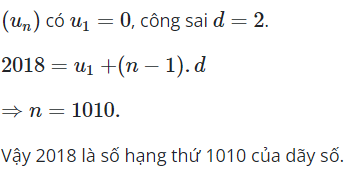
Câu 27:
19/07/2024Một khu rừng có trữ lượng gỗ là mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?
 Xem đáp án
Xem đáp án
Chọn C.
Ta có trữ lượng gỗ của khu rừng sau mỗi năm lập thành một cấp số nhân với
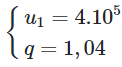
Trữ lượng gỗ sau năm năm là số hạng thứ năm của cấp số nhân.
Ta có ![]()
Câu 28:
22/07/2024Tổng có giá trị bằng
 Xem đáp án
Xem đáp án
Chọn C.
Ta có ![]() là tổng của một cấp số nhân với số hạng đầu là 1, công bội
là tổng của một cấp số nhân với số hạng đầu là 1, công bội
Do đó
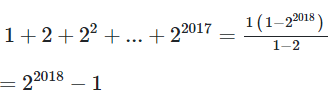
Câu 29:
21/07/2024Tổng có giá trị bằng
 Xem đáp án
Xem đáp án
Chọn D.
Ta có ![]() là tổng của một cấp số nhân với số hạng đầu là 1, công bội
là tổng của một cấp số nhân với số hạng đầu là 1, công bội
Do đó
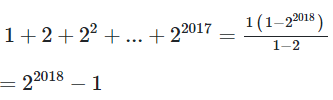
Có thể bạn quan tâm
- Trắc nghiệm Ôn chương 3 (có đáp án) (1168 lượt thi)
Các bài thi hot trong chương
- 70 câu trắc nghiệm Dãy số, Cấp số cộng, Cấp số nhân cơ bản (P1) (1987 lượt thi)
- 70 câu trắc nghiệm Dãy số, Cấp số cộng, Cấp số nhân nâng cao (P1) (949 lượt thi)
- Trắc nghiệm Cấp số nhân (có đáp án) (781 lượt thi)
- Trắc nghiệm Dãy số (có đáp án) (707 lượt thi)
- Trắc nghiệm Cấp số cộng (có đáp án) (636 lượt thi)
- Trắc nghiệm Cấp số cộng có đáp án (Nhận biết) (503 lượt thi)
- Trắc nghiệm Cấp số cộng có đáp án (phần 2) (495 lượt thi)
- Trắc nghiệm Phương pháp quy nạp toán học (có đáp án) (453 lượt thi)
- Trắc nghiệm Phương pháp quy nạp toán học có đáp án (422 lượt thi)
- Trắc nghiệm Cấp số nhân có đáp án (Thông hiểu) (402 lượt thi)