Trắc nghiệm Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước
-
348 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Chọn phương án đúng nhất trong các phương án sau?
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
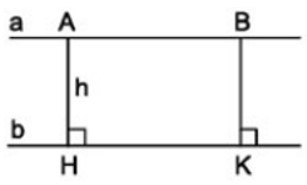
Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia. h là khoảng cách giữa hai đường thẳng song song a và b.
Câu 2:
18/07/2024Cho hai đường thẳng song song a và b và có khoảng cách 3cm. Điểm A thuộc đường thẳng a thì:
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Do a // b cách nhau một khoảng 3cm và điểm A thuộc đường thẳng a nên khoảng cách từ điểm A đến đường thẳng b bằng 3cm.
Câu 3:
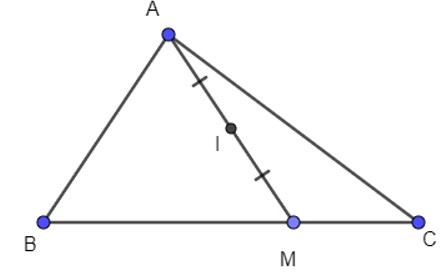
15/07/2024Cho tam giác ABC, M là một điểm bất kì nằm trên BC. Lấy I là trung điểm đoạn thẳng AM. Hỏi khi M di chuyển trên BC thì I di chuyển trên đường thẳng nào?
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
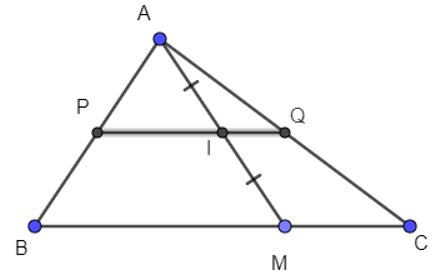
Gọi P là trung điểm AB, Q là trung điểm của AC
Suy ra PQ là đường trung bình của tam giác ABC.
Do đó PQ //BC (1)
Xét tam giác ABM có:
P là trung điểm AB
I là trung điểm AM
Nên PI là đường trung bình của tam giác ABM
Suy ra PI // BM hay PI // BC (2)
Từ (1) và (2) suy ra I thuộc PQ.
Mà PQ cố định
Vậy khi M di chuyển trên BC thì I di chuyển trên đường trung bình của tam giác ABC.
Câu 4:
15/07/2024Chọn phương án đúng trong các phương án sau
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Tính chất:
Các điểm cách đường thẳng b một khoảng bằng h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h.
Nhận xét: Từ định nghĩa về khoảng cách hai đường thẳng song song và tính chất trên ta có: Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.
Câu 5:
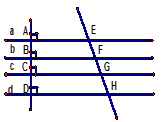
16/07/2024Cho hình dưới đây, trong đó các đường thẳng a,b,c,d song song với nhau. Nếu các đường thẳng a,b,c,d song song cách đều thì :
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Định lí:
+ Nếu các đường thẳng song song cách đều cắt một đường thằng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
+ Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
⇒ EF = FG = GH
Câu 6:
16/07/2024Cho Δ ABC có D là trung điểm của AB, kẻ DE//BC ( E thuộc AC ). Nhận xét nào sau đây đúng?
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
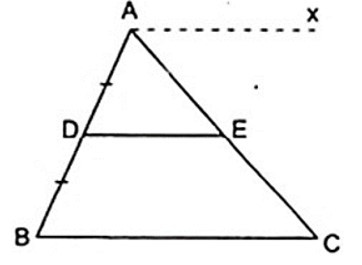
Do DE//BC theo giả thiết nên vẽ thêm Ax//DE thì
Ax//DE//BC ( 1 )
Vì D là trung điểm của AB nên AD = BD ( 2 )
Từ ( 1 ), ( 2 ) suy ra ba đường Ax, DE, BC là ba đường song song cách đều nên nó chắn trên đường thẳng AC hai đoạn thẳng liên tiếp bằng nhau là AE = EC.
Câu 7:
19/07/2024Tập hợp các điểm A cách đều đường thẳng b cho trước một đoạn 5,5 cm là
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Tập hợp các điểm A cách đều đường thẳng b cho trước một đoạn 5,5 cm là: Đường thẳng song song với đường thẳng b và cách b một đoạn 5,5 cm.
Câu 8:
22/07/2024Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K lần lượt là các chân đường cao kẻ từ kẻ từ B và C đến đường thẳng DE. Phát biểu nào sau đây là đúng?
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
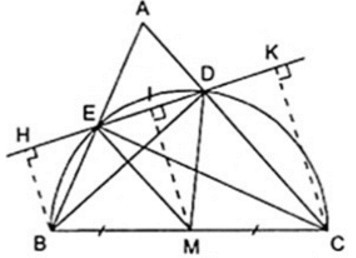
Vì BD, CE là đường cao của tam giác ABC nên
do đó Δ BDC vuông tại D, Δ CEB vuông tại E.
Gọi M là trung điểm của BC
⇒ DM, EM là đường trung tuyến ứng với cạnh huyền của Δ BDC và Δ CEB.
Áp dụng tính chất của đường trung tuyến ứng với cạnh huyền của hai tam giác trên ta được:
cân tại M.
Từ giả thiết ta có tứ giác BHKC là hình thang vuông nên vẽ MI ⊥ DE
thì BH//MI//CK (1) (vì cùng vuông góc với đường thẳng DE)
Mà ta có BM = MC (2) (do ta vẽ hình trên)
Từ (1),(2) suy ra BH, MI, CK là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK (3).
Áp dụng tính chất của đường cao ứng với cạnh đáy của tam giác cân MDE ta được:
EI = ID (4)
Trừ theo vế đẳng thức (3) cho (4), ta được: HE = DK.