Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit có đáp án (Nhận biết)
Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit có đáp án (Nhận biết)
-
348 lượt thi
-
20 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 4:
23/07/2024Tìm tập nghiệm S của bất phương trình
 Xem đáp án
Xem đáp án
Vì nên suy ra x>0
Đáp án cần chọn là: A
Câu 5:
22/07/2024Tập nghiệm của bất phương trình là
 Xem đáp án
Xem đáp án
Vì
Vậy tập nghiệm của bất phương trình là
Đáp án cần chọn là: C
Câu 16:
26/11/2024Tập nghiệm của bất phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải:

*Phương pháp giải:
Ta có BPT
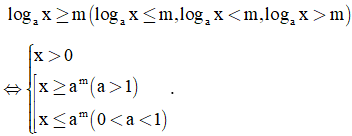
*Lý thuyết nắm thêm về bất phương trình mũ và bất phương trình logarit
1. Định nghĩa
Bất phương trình lôgarit là bất phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
2. Phương trình và bất phương trình lôgarit cơ bản: cho
Bất phương trình lôgarit cơ bản có dạng:
3. Phương pháp giải phương trình và bất phương trình lôgarit
+ Đưa về cùng cơ số
Nếu thì
Nếu thì
+ Đặt ẩn phụ
+ Mũ hóa
+ Phương pháp hàm số và đánh giá
Xem thêm các bài viết liên quan hay, chi tiết:
Bất phương trình logarit và cách giải các dạng bài tập (2024)
Có thể bạn quan tâm
- Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit (có đáp án) (532 lượt thi)
- 30 câu trắc nghiệm: Bất phương trình mũ và bất phương trình lôgarit có đáp án (338 lượt thi)
- Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit có đáp án (Nhận biết) (347 lượt thi)
- Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit có đáp án (Thông hiểu) (359 lượt thi)
- Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit có đáp án (Vận dụng) (302 lượt thi)
- Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit có đáp án (376 lượt thi)
- Trắc nghiệm Ôn tập chương II có đáp án (Thông hiểu) (290 lượt thi)
- Trắc nghiệm Ôn tập chương II có đáp án (Vận dụng) (313 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Logarit có đáp án (Thông hiểu) (1086 lượt thi)
- 200 câu trắc nghiệm Hàm số mũ và Logarit cơ bản (P1) (791 lượt thi)
- Trắc nghiệm Logarit có đáp án (Nhận biết) (635 lượt thi)
- Trắc nghiệm Logarit (có đáp án) (567 lượt thi)
- Trắc nghiệm Lũy thừa có đáp án (Nhận biết) (554 lượt thi)
- Trắc nghiệm Lũy thừa có đáp án (Vận dụng) (547 lượt thi)
- Trắc nghiệm Lũy thừa (có đáp án) (469 lượt thi)
- Trắc nghiệm Logarit có đáp án (463 lượt thi)
- Trắc nghiệm Hàm số mũ. Hàm số Logarit (có đáp án) (453 lượt thi)
- Trắc nghiệm Logarit có đáp án (Vận dụng) (450 lượt thi)
