Thi Online Trắc nghiệm Toán 10 CTST Bài 3. Tích của một số với một vectơ có đáp án
Dạng 4: Phân tích một vectơ thành hai hay nhiều vectơ cho trước có đáp án
-
1191 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích 
qua các vectơ →a và →b ta được biểu thức là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
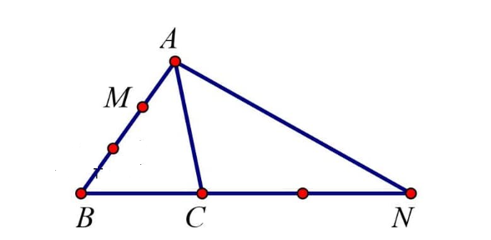
Theo đề bài: CN = 2BC nên →BN=3→BC
Ta có:
→AN=→AB+→BN=→AB+3→BC=→AB+3(→AC−→AB)=−2→AB+3→AC=−2→a+3→b.
Câu 2:
22/07/2024Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích qua các vectơ →a và →b ta được biểu thức là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
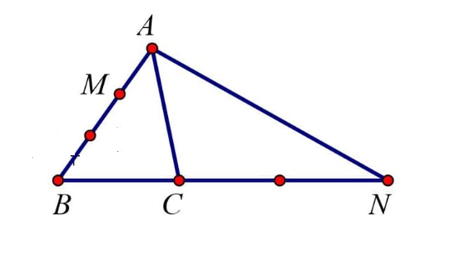
Theo đề bài:
AB = 3AM nên →AM=13→AB⇒→MA=−13→AB
CN = 2BC nên →BN=3→BC
Ta có:
→AN=→AB+→BN=→AB+3→BC=→AB+3(→AC−→AB)=−2→AB+3→AC=−2→a+3→b
→MN=→MA+→AN=−13→a−2→a+3→b=−73→a+3→b.
Câu 3:
21/07/2024Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. Phân tích vectơ →BN qua các vectơ →AB và →AC.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
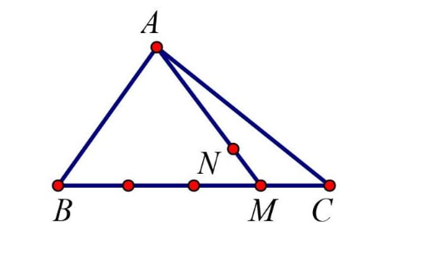
Theo đề bài ta có:
→BM=34→BC và →AN=57→AM
Ta có:
→AM=→AB+→BM=→AB+34→BC=→AB+34(→AC−→AB)=14→AB+34→AC
→BN=→BA+→AN=−→AB+57→AM=−→AB+57(14→AB+34→AC)=−2328→AB+1528→AC
Câu 4:
12/07/2024Cho tam giác ABC, G là trọng tâm của tam giác ABC. Phân tích vectơ →GC qua các vectơ →GA và →GB.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
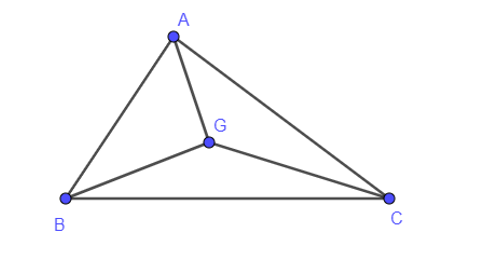
Theo đề bài ta có: G là trọng tâm của tam giác ABC nên
→GA+→GB+→GC=→0⇔→GC=−→GA−→GB.
Câu 5:
22/07/2024Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. G là trọng tâm của tam giác ABC. Phân tích vectơ →MN qua các vectơ →GA và →GB.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
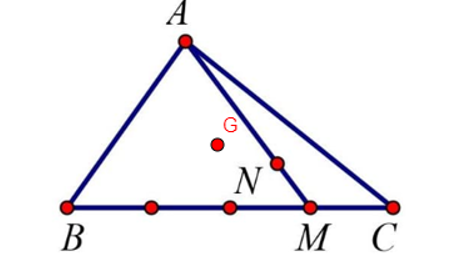
Theo đề bài ta có:
→BM=34→BC và →MN=−27→AM.
Vì G là trọng tâm tam giác ABC nên →GA+→GB+→GC=→0⇔→GC=−→GA−→GB
Ta có:
→AM=→AB+→BM=→AB+34→BC=→AB+34(→AC−→AB)=14→AB+34→AC
→MN=−27→AM=−27(14→AB+34→AC)
=−114(→GB−→GA)−314(→GC−→GA)
=−114(→GB−→GA)−314(−→GA−→GB−→GA)
=12→GA+17→GB.
Câu 6:
13/07/2024Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ →AN qua các vectơ →AB và →AC.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
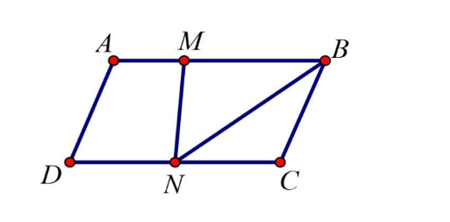
Ta có: CD = 2CN và N nằm trên cạnh CD nên →CN=12→CD.
Mà ABCD là hình bình hành nên →AB=→DC⇔→AB=−→CD.
Do đó, →CN=−12→AB.
Theo quy tắc ba điểm ta có: →AN=→AC+→CN=→AC−12→AB.
Câu 7:
21/07/2024Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ →MN qua các vectơ →AB và →AC.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
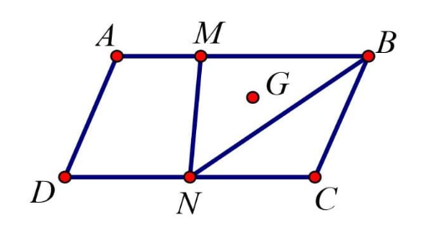
Vì AB = 3AM và M nằm trên cạnh AB nên →MA=−13→AB.
Ta có: →AN=→AC+→CN=→AC−12→AB
Do đó ta có: →MN=→MA+→AN=−13→AB+→AC−12→AB=−56→AB+→AC.
Câu 8:
16/07/2024Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ →AG qua các vectơ →AB và →AC ta được →AG=ab→AB+cd→AC với ab và cd là các phân số tối giản. Khi đó ta có: ab+cd=?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
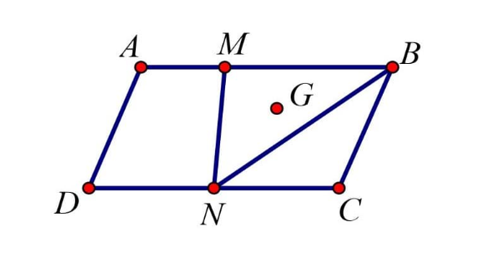
Vì AB = 3AM và M nằm trên cạnh AB nên →AM=13→AB.
Ta có: →AN=→AC+→CN=→AC−12→AB.
G là trọng tâm tam giác MNB nên ta có:
3→AG=→AM+→AN+→AB=13→AB+(→AC−12→AB)+→AB=56→AB+→AC
⇔→AG=518→AB+13→AC.
Do đó ab=518 và cd=13.
Suy ra ab+cd=518+13=1118.
Câu 9:
09/10/2024Cho AK và BM là hai trung tuyến của tam giác ABC. Phân tích vectơ →AB theo hai vectơ →AK=→u và →BM=→v ta được biểu thức là:
Xem đáp án
Đáp án đúng: C.
*Phương pháp giải:
- Nắm kỹ lý thuyết về vectơ và dạng bài tính tổng hiệu hai vecto. Tính chất trung điểm, đường trung bình của tam giác để làm
*Lời giải:
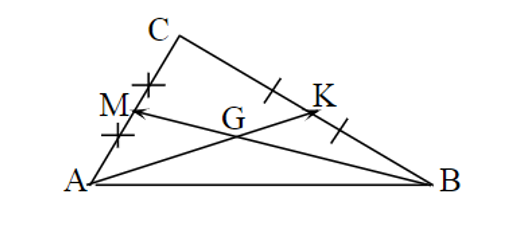
Ta có:
→AB=→AK+→KB=→AK+→KM+→MB
Mà →KM=−12→AB (vì MK là đường trung bình của tam giác ABC)
Do đó:
→AB=→AK−12→AB−→BM
⇔→AB+12→AB=→AK−→BM
⇔32→AB=→AK−→BM
⇔→AB=23→AK−23→BM=23→u−23→v.
*Một số dạng bài về tích của vectơ với một số
*Lý thuyết cần nắm:
- Tích của vectơ với một số: Cho số k≠0 và vectơ →a≠→0. Tích của vectơ →a với số k là một vectơ, kí hiệu là k→a, cùng hướng với →a nếu k > 0, ngược lại, ngược hướng với →a nếu k < 0 và có độ dài bằng |k||→a|.
- Tính chất: Với hai vectơ →a và →b bất kì, với mọi số h và k, ta có:
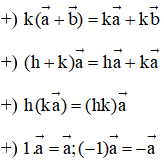
- Quy tắc trung điểm: Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có: →MA+→MB=2→MI
- Quy tắc trọng tâm: Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có: →MA+→MB+→MC=3→MG
Dạng 1: Tính độ dài vectơ khi biết tích vectơ với một số.
* Phương pháp giải: Sử dụng định nghĩa tích của vectơ với một số, các quy tắc về tổng, hiệu của các vectơ và các hệ thức lượng, định lý Py-ta-go để tính độ dài vectơ đó.
Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước.
* Phương pháp giải: Biến đổi đẳng thức đã cho về dạng →AM=→u trong đó A là một điểm cố định, →u cố định và dựng điểm M là điểm thỏa mãn →AM=→u.
Xem thêm các bài viết liên quan hay, chi tiết
Giải Toán 10 Bài 3 (Chân trời sáng tạo): Tích của một số với một vectơ
Chuyên đề Vectơ lớp 10 (có đáp án)
Câu 10:
19/07/2024Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2→IC=3→BI. Phân tích vectơ →AI theo hai vectơ →AB và →AC.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có: 2→IC=3→BI
⇔2(→AC−→AI)=3(→AI−→AB)
⇔2→AC−2→AI=3→AI−3→AB
⇔5→AI=3→AB+2→AC
⇔→AI=35→AB+25→AC.