Thi Online Trắc nghiệm Toán 10 CTST Bài 3. Tích của một số với một vectơ có đáp án
Dạng 5: Chứng minh hai vectơ cùng phương có đáp án
-
905 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
12/07/2024Cho và không cùng phương và hai vectơ và . Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
Vì – 2 < 0
Do đó, và cùng phương, ngược hướng.
Câu 2:
12/07/2024Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
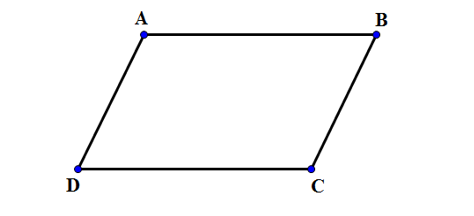
Xét hình bình hành ABCD có:
AB // CD
Do đó, và cùng phương, ngược hướng.
Câu 3:
19/07/2024Cho hình vuông ABCD tâm O. Khẳng định nào sau đây là sai ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Vì ABCD là hình vuông nên và cùng phương, ngược hướng; và cùng phương, ngược hướng.
Lại có và có cùng giá là đường thẳng AC.
Do đó, và cùng phương.
Vậy đáp án C sai.
Câu 4:
12/07/2024Cho các vectơ và không cùng phương và , và . Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có:
Vì – 2 < 0
Vậy , cùng phương, ngược hướng.
Câu 5:
12/07/2024Cho các vectơ và không cùng phương và và . Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
Giả sử tồn tại số thực k sao cho .
Mà và không cùng phương nên ta có:
Vậy không tồn tại k thỏa mãn.
Do đó, và không cùng phương.
Câu 6:
14/07/2024Cho các vectơ và không cùng phương và: , và . Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
Có: 2 > 0
Do đó, , cùng phương, cùng hướng.
Câu 7:
18/07/2024Cho các vectơ , , không cùng phương và: , và . Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Có: 2 > 0
Do đó, , cùng phương, cùng hướng.
Câu 8:
16/07/2024Cho các vectơ , không cùng phương và: , và . Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Giả sử tồn tại số thực k sao cho:
Mà , không cùng phương nên điều này tương đương với:
Vậy không tồn tại số thực k thỏa mãn
Do đó, , không cùng phương.
Câu 9:
12/07/2024Cho hình chữ nhật ABCD, M là trung điểm của CD, N là trung điểm của AB. Số vectơ khác vectơ – không, có điểm đầu và điểm cuối là đỉnh của hình chữ nhật ABCD và cùng phương với là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
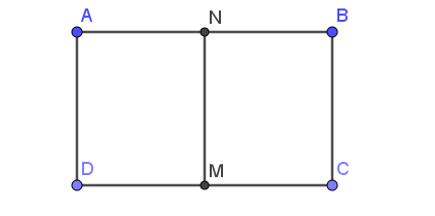
Xét hình chữ nhật ABCD có:
M là trung điểm của CD, N là trung điểm của AB nên MN // AD // BC.
Do đó, các vectơ cùng phương với và có điểm đầu và điểm cuối là đỉnh của hình chữ nhật ABCD cần có giá là đường thẳng AD hoặc BC.
Các vectơ thỏa mãn yêu cầu đề bài là: .
Vậy có 4 vectơ.
Câu 10:
22/07/2024Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ – không, có điểm đầu và điểm cuối là đỉnh của hình lục giác đều ABCDEF và cùng phương với vectơ là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Do ABCDEF là lục giác đều tâm O nên ta có: BE // CD // AF.
Hơn nữa đường thẳng OB trùng với đường thẳng BE.
Suy ra OB // CD // AF.
Do đó các vectơ khác vectơ – không, có điểm đầu và điểm cuối là đỉnh của hình lục giác đều ABCDEF và cùng phương với vectơ là: .
Vậy có 6 vectơ thỏa mãn.