10 câu hỏi trắc nghiệm thuộc Dạng 3: Chứng minh đẳng thức vectơ có đáp án

Câu 1:

21/07/2024

Cho tam giác ABC. Gọi M là trung điểm của AB và N là điểm trên cạnh AC sao cho NC = 2NA. Gọi K là trung điểm của MN. Khẳng định nào sau đây đúng ?

A. $\vec{A K} = \frac{1}{4} \vec{A B} + \frac{1}{6} \vec{A C}$

B. $\vec{A K} = \frac{1}{2} \vec{A B} + \frac{1}{6} \vec{A C}$

C. $\vec{A K} = \frac{1}{3} \vec{A B} + \frac{1}{6} \vec{A C}$

D. $\vec{A K} = \frac{1}{4} \vec{A B} + \frac{1}{3} \vec{A C}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Cho tam giác ABC. Gọi M là trung điểm của AB và N là điểm trên cạnh AC sao cho (ảnh 1)

Do M là trung điểm AB nên $\vec{A M} = \frac{1}{2} \vec{A B}$ .

Vì NC = 2NA nên $\vec{A N} = \frac{1}{3} \vec{A C}$ .

Ta có:

$\vec{A K} = \frac{1}{2} (\vec{A M} + \vec{A N})$ (vì K là trung điểm của MN)

$= \frac{1}{2} (\frac{1}{2} \vec{A B} + \frac{1}{3} \vec{A C})$

$= \frac{1}{4} \vec{A B} + \frac{1}{6} \vec{A C}$

Vậy $\vec{A K} = \frac{1}{4} \vec{A B} + \frac{1}{6} \vec{A C}$ .

Câu 2:

13/07/2024

Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?

A. $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0}$

B. $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{ A B}$

C. $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{A C}$

D. $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{B C}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Ta có:

$\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D}$

$= (\vec{O A} + \vec{O B}) + (\vec{O C} + \vec{O D})$

$= 2 \vec{O E} + 2 \vec{O F}$ (do E, F lần lượt là trung điểm của AB, CD)

$= 2 (\vec{O E} + \vec{O F}) = 2. \vec{0} = \vec{0}$ (do O là trung điểm của EF).

Vậy $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0}$ .

Câu 3:

19/07/2024

Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?

A. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = \vec{M O}$

B. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 2 \vec{M O}$

C. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 3 \vec{M O}$

D. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Ta có:

$\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D}$

$= (\vec{O A} + \vec{O B}) + (\vec{O C} + \vec{O D})$

$= 2 \vec{O E} + 2 \vec{O F}$ (do E, F lần lượt là trung điểm của AB, CD)

$= 2 (\vec{O E} + \vec{O F}) = 2. \vec{0} = \vec{0}$ (do O là trung điểm của EF)

Do đó, ta có:

$\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D}$

$= (\vec{M O} + \vec{O A}) + (\vec{M O} + \vec{O B}) + (\vec{M O} + \vec{O C}) + (\vec{M O} + \vec{O D})$ (quy tắc ba điểm)

$= 4 \vec{M O} + (\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D}) = 4 \vec{M O}$ .

Vậy $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$ .

Câu 4:

12/07/2024

Cho tam giác ABC và G là trọng tâm. Và điểm O sao cho $\vec{O A} + \vec{O B} + \vec{O C} = \vec{O H}$ . Khẳng định nào sau đây là đúng ?

A. $\vec{O H} = 2 \vec{O G}$

B. $\vec{O H} = 3 \vec{O G}$

C. $\vec{O H} = - \vec{O G}$

D. $\vec{O H} = \vec{O G}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Vì G là trọng tâm của tam giác ABC thì với O là một điểm bất kì ta luôn có $\vec{O A} + \vec{O B} + \vec{O C} = 3 \vec{O G}$ .

Do đó ta có: $\vec{O H} = \vec{O A} + \vec{O B} + \vec{O C} = 3 \vec{O G}$ .

Vậy $\vec{O H} = 3 \vec{O G}$ .

Câu 5:

21/07/2024

Cho tam giác ABC và G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp của tam giác. Gọi D là điểm đối xứng của A qua O. Biểu thức $\vec{O B} + \vec{O C}$ bằng biểu thức nào dưới đây?

A. $2 \vec{O H}$ $+ \vec{H D}$

B. $\vec{O H}$ $+ \vec{H D}$

C. $3 \vec{O H}$ $+ \vec{H D}$

D. $- \vec{O H}$ $+ \vec{H D}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Xét đường tròn tâm O ngoại tiếp tam giác ABC

Có: $\hat{A B D} = 90^{o}$ (góc nội tiếp chắn nửa đường tròn)

Do đó, BD vuông góc với AB.

Mà CH vuông góc với AB vì H là trực tâm.

Do đó, BD // CH.

Chứng minh tương tự ta có: CD // BH.

Do đó, HBDC là hình bình hành

$\Rightarrow \vec{H B} + \vec{H C} = \vec{H D}$ (quy tắc hình bình hành)

Ta có: $\vec{O B} + \vec{O C} = (\vec{O H} + \vec{H B}) + (\vec{O H} + \vec{H C})$ (quy tắc ba điểm)

$= 2 \vec{O H} + (\vec{H B} + \vec{H C}) = 2 \vec{O H} + \vec{H D}$ .

Vậy $\vec{O B} + \vec{O C}$ = $2 \vec{O H}$ + $\vec{H D}$ .

Câu 6:

12/07/2024

Cho tam giác ABC và G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp của tam giác. Gọi D là điểm đối xứng của A qua O. Tính $\vec{H A} - \vec{H B} - \vec{H C}$ .

A. $2 \vec{O A}$

B. $\vec{O A}$

C. $3 \vec{O A}$

D. $- \vec{O A}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

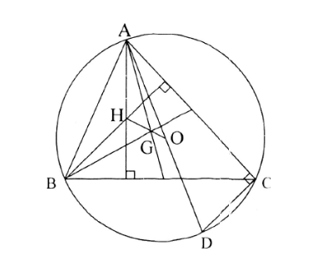
Cho tam giác ABC và G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp (ảnh 1)

Xét đường tròn tâm O ngoại tiếp tam giác ABC

Có: $\hat{A B D} = 90^{o}$ (hai góc nội tiếp cùng chắn nửa đường tròn)

Do đó, BD vuông góc với AB

MÀ CH vuông góc với AB vì H là trực tâm

Do đó, BD // CH

Chứng minh tương tự ta có: CD // BH.

Do đó, HBDC là hình bình hành.

$\Rightarrow \vec{H B} + \vec{H C} = \vec{H D}$ (quy tắc hình bình hành)

Ta có: $\vec{H A} - \vec{H B} - \vec{H C} = \vec{H A} - (\vec{H B} + \vec{H C}) = \vec{H A} - \vec{H D} = \vec{D A} = 2 \vec{O A}$ (do A đối xứng với D qua O nên O là trung điểm của AD).

Vậy $\vec{H A} - \vec{H B} - \vec{H C} = 2 \vec{O A}$ .

Câu 7:

14/07/2024

Cho tam giác ABC có D, E, F lần lượt là trung điểm của BC, CA, AB. Khẳng định nào sau đây là đúng ?

A. $\vec{M A} + \vec{M B} + \vec{M C} = \vec{M D} - \vec{M E} - \vec{M F}$

B. $\vec{M A} + \vec{M B} + \vec{M C} = \vec{M D} + \vec{M E} - \vec{M F}$

C. $\vec{M A} + \vec{M B} + \vec{M C} = \vec{M D} - \vec{M E} + \vec{M F}$

D. $\vec{M A} + \vec{M B} + \vec{M C} = \vec{M D} + \vec{M E} + \vec{M F}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

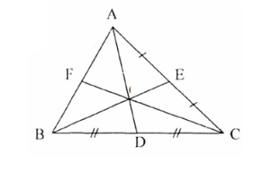
Cho tam giác ABC có D, E, F lần lượt là trung điểm của BC, CA, AB. Khẳng định nào sau (ảnh 1)

Ta có:

Do F là trung điểm của AB nên $\vec{M A} + \vec{M B} = 2 \vec{M F}$ .

Do D là trung điểm của BC nên $\vec{M B} + \vec{M C} = 2 \vec{M D}$ .

Do E là trung điểm của AC nên $\vec{M C} + \vec{M A} = 2 \vec{M E}$ .

Từ đó, ta có:

$\vec{M A} + \vec{M B} + \vec{M B} + \vec{M C} + \vec{M C} + \vec{M A} = 2 \vec{M F} + 2 \vec{M D} + 2 \vec{M E}$

$\Leftrightarrow 2 (\vec{M A} + \vec{M B} + \vec{M C}) = 2 (\vec{M F} + \vec{M D} + \vec{M E})$

$\Leftrightarrow \vec{M A} + \vec{M B} + \vec{M C} = \vec{M D} + \vec{M E} + \vec{M F}$ .

Câu 8:

12/07/2024

Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ. Đẳng thức nào sau đây đúng.

A. $\vec{A C} + \vec{B D} = \vec{I J}$

B. $\vec{A C} + \vec{B D} = 2 \vec{I J}$

C. $\vec{A C} + \vec{B D} = \vec{J I}$

D. $\vec{A C} + \vec{B D} = 2 \vec{J I}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

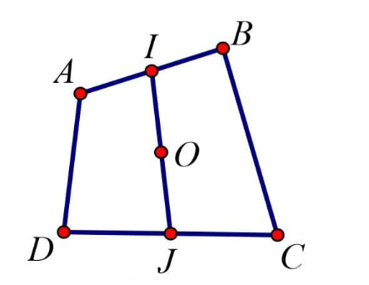
Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm (ảnh 1)

Theo quy tắc ba điểm ta có: $\vec{A C} = \vec{A I} + \vec{I J} + \vec{J C}$ ; $\vec{B D} = \vec{B I} + \vec{I J} + \vec{J D}$

Mà I và J là trung điểm của AB, CD nên ta có: $\vec{A I} + \vec{B I} = \vec{0}; \vec{J C} + \vec{J D} = \vec{0}$

Nên ta có:

$\vec{A C} + \vec{B D} = (\vec{A I} + \vec{B I}) + (\vec{J C} + \vec{J D}) + 2 \vec{I J} = 2 \vec{I J}$ .

Vậy $\vec{A C} + \vec{B D} = 2 \vec{I J}$ .

Câu 9:

12/07/2024

Cho 4 điểm A, B, C, D phân biệt không thẳng hàng. Gọi I, J lần lượt là trung điểm của BC và CD. Tính: $2 (\vec{A B} + \vec{A I} + \vec{J A} + \vec{D A}) = ?$

A. $3 \vec{D B}$

B. $2 \vec{D B}$

C. $\vec{D B}$

D. $4 \vec{D B}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Xét tam giác BCD có:

I, J lần lượt là trung điểm của BC và CD

Do đó, IJ lần lượt là đường trung bình của tam giác BCD

$\Rightarrow \vec{J I} = \frac{1}{2} \vec{D B}$ .

Ta có:

$2 (\vec{A B} + \vec{A I} + \vec{J A} + \vec{D A})$

$= 2 [(\vec{D A} + \vec{A B}) + (\vec{J A} + \vec{A I})]$

$= 2 (\vec{D B} + \vec{J I})$ (quy tắc ba điểm)

$= 2 \vec{D B} + 2 \vec{J I}$

$= 2 \vec{D B} + 2. \frac{1}{2} \vec{D B}$

$= 3 \vec{D B}$ .

Vậy $2 (\vec{A B} + \vec{A I} + \vec{J A} + \vec{D A}) = 3 \vec{D B}$ .

Câu 10:

21/07/2024

Cho tam giác ABC, có trung tuyến AM, I là trung điểm của AM. Tính $2 \vec{O A} + \vec{O B} + \vec{O C} = ?$

A. $\vec{O I}$

B. $2 \vec{O I}$

C. $3 \vec{O I}$

D. $4 \vec{O I}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

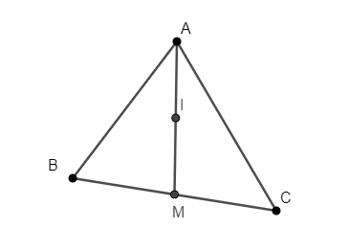
Cho tam giác ABC, có trung tuyến AM, I là trung điểm của AM. Tính 2 vecto OA+ OB+OC=? (ảnh 1)

AM là trung tuyến nên M là trung điểm của BC, do đó $\vec{I B} + \vec{I C} = 2 \vec{I M}$

Vì I là trung điểm của AM nên $\vec{I A} + \vec{I M} = \vec{0}$ .

Ta có:

$2 \vec{O A} + \vec{O B} + \vec{O C}$

$= 2 (\vec{O I} + \vec{I A}) + (\vec{O I} + \vec{I B}) + (\vec{O I} + \vec{I C})$ (quy tắc ba điểm)

$= 4 \vec{O I} + 2 \vec{I A} + (\vec{I B} + \vec{I C})$

$= 4 \vec{O I} + 2 \vec{I A} + 2 \vec{I M}$

$= 4 \vec{O I} + 2 (\vec{I A} + \vec{I M})$

$= 4 \vec{O I} + 2. \vec{0} = 4 \vec{O I}$ .

Vậy $2 \vec{O A} + \vec{O B} + \vec{O C} = 4 \vec{O I}$ .

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3