Câu hỏi:
12/07/2024 204
Cho tam giác ABC, G là trọng tâm của tam giác ABC. Phân tích vectơ →GC qua các vectơ →GA và →GB.
Cho tam giác ABC, G là trọng tâm của tam giác ABC. Phân tích vectơ →GC qua các vectơ →GA và →GB.
A. →GC = →GA+→GB;
A. →GC = →GA+→GB;
B. →GC = −→GA−→GB;
C. →GC = −→GA+→GB;
D. →GC = →GA−→GB.
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: B.
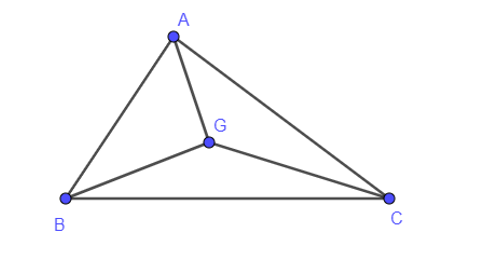
Theo đề bài ta có: G là trọng tâm của tam giác ABC nên
→GA+→GB+→GC=→0⇔→GC=−→GA−→GB.
Hướng dẫn giải:
Đáp án đúng là: B.
Theo đề bài ta có: G là trọng tâm của tam giác ABC nên
→GA+→GB+→GC=→0⇔→GC=−→GA−→GB.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho AK và BM là hai trung tuyến của tam giác ABC. Phân tích vectơ →AB theo hai vectơ →AK=→u và →BM=→v ta được biểu thức là:
Cho AK và BM là hai trung tuyến của tam giác ABC. Phân tích vectơ →AB theo hai vectơ →AK=→u và →BM=→v ta được biểu thức là:
Câu 2:
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ →AG qua các vectơ →AB và →AC ta được →AG=ab→AB+cd→AC với ab và cd là các phân số tối giản. Khi đó ta có: ab+cd=?
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ →AG qua các vectơ →AB và →AC ta được →AG=ab→AB+cd→AC với ab và cd là các phân số tối giản. Khi đó ta có: ab+cd=?
Câu 3:
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ →AN qua các vectơ →AB và →AC.
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ →AN qua các vectơ →AB và →AC.
Câu 4:
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. Phân tích vectơ →BN qua các vectơ →AB và →AC.
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. Phân tích vectơ →BN qua các vectơ →AB và →AC.
Câu 5:
Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích 
qua các vectơ →a và →b ta được biểu thức là:
Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích qua các vectơ →a và →b ta được biểu thức là:
Câu 6:
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ →MN qua các vectơ →AB và →AC.
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ →MN qua các vectơ →AB và →AC.
Câu 7:
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. G là trọng tâm của tam giác ABC. Phân tích vectơ →MN qua các vectơ →GA và →GB.
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. G là trọng tâm của tam giác ABC. Phân tích vectơ →MN qua các vectơ →GA và →GB.
Câu 8:
Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2→IC=3→BI. Phân tích vectơ →AI theo hai vectơ →AB và →AC.
Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2→IC=3→BI. Phân tích vectơ →AI theo hai vectơ →AB và →AC.
Câu 9:
Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích qua các vectơ →a và →b ta được biểu thức là:
Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích qua các vectơ →a và →b ta được biểu thức là:
