Thi Online Trắc nghiệm Toán 10 Bài tập cuối chương 8 có đáp án
Trắc nghiệm Toán 10 Bài tập cuối chương 8 có đáp án
-
373 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Cho các số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên lẻ gồm 4 chữ số đôi một khác nhau
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Gọi số cần lập , a ≠ 0.
Công đoạn 1, chọn số d có 3 cách chọn (Vì là số lẻ nên d chỉ có thể chọn một trong 3 số 1; 3; 5).
Công đoạn 2, chọn số a có 5 cách chọn (Vì a ≠ 0; a ≠ d nên a không được chọn số 0 và số d đã chọn).
Công đoạn 3, chọn số b có 5 cách chọn (Vì b ≠ a; b ≠ d nên b không được chọn lại số a, d đã chọn).
Công đoạn 4, chọn số c có 4 cách chọn (Vì c ≠ a; c ≠ b; c ≠ d nên c không được chọn lại số a, b, d đã chọn).
Tổng kết, áp dụng quy tắc nhân ta có số các số tự nhiên lẻ gồm 4 chữ số đôi một khác nhau là: 3.5.5.4 = 300.
Câu 2:
20/07/2024Cho các số 1; 2; 3; 4; 5; 6; 7; 8 có thể lập được bao nhiêu số tự nhiên lẻ gồm 5 chữ số đôi một khác nhau sao các số này lẻ không chia hết cho 5.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Gọi số cần lập , a ≠ 0; a, b, c, d, e ∈ {1; 2; 3; 4; 5; 6; 7; 8}.
Công đoạn 1, chọn số e có 3 cách chọn (Vì là số lẻ và không chia hết cho 5 nên e chỉ có thể chọn một trong 3 số 1; 3; 7).
Công đoạn 2, chọn số a có 7 cách chọn (Vì a ≠ 0;a ≠ e nên a không được chọn số e đã chọn).
Công đoạn 3, chọn số b có 6 cách chọn (Vì b ≠ a; b ≠ e nên b không được chọn lại số a, e đã chọn).
Công đoạn 4, chọn số c có 5 cách chọn (Vì c ≠ a; c ≠ b; c ≠ e nên c không được chọn lại số a, b, e đã chọn).
Công đoạn 5, chọn số d có 4 cách chọn (Vì d ≠ a; d ≠ b; d ≠ c; d ≠ e nên d không được chọn lại số a, b, c, e đã chọn).
Vậy áp dụng quy tắc nhân ta có số các số tự nhiên gồm 5 chữ số đôi một khác nhau sao các số này lẻ không chia hết cho 5 là: 3.7.6.5.4 = 2520 (số).
Câu 3:
23/07/2024Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7 và 8 quả cầu vàng được đánh số từ 1 đến 8. Hỏi có bao nhiêu cách lấy ra 3 quả cầu khác màu và khác số.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta chọn các quả cầu theo trình tự sau:
Công đoạn 1. Chọn quả cầu xanh: 7 cách chọn (Vì cầu xanh được chọn tuỳ ý từ 1 đến 7).
Công đoạn 2, Chọn quả cầu vàng: có 7 cách chọn (Vì số đánh trên cầu vàng không được chọn lại số đã đánh trên quả cầu xanh đã chọn).
Công đoạn 3, Chọn quả cầu đỏ: có 8 cách chọn (Vì số trên quả cầu đỏ chọn không được chọn lại các số mà quả cầu xanh và quả cầu vàng đã chọn).
Vậy số cách lấy ra 3 quả cầu khác màu và khác số là 7.7.8 = 392 cách chọn.
Câu 5:
15/07/2024Lớp 10A có 20 học sinh nam và 25 học sinh nữ. Thầy giáo có bao nhiêu cách chọn ra hai học sinh để thi đấu cầu lông đôi nam nữ.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Vì thi đấu cầu lông đôi nam, nữ nên thầy giáo phải chọn 1 nam và 1 nữ
Công đoạn 1, chọn học sinh nam có 20 cách
Công đoạn 2, chọn học sinh nữ có 25 cách
Vậy áp dụng quy tắc nhân có 20.25 = 500 (cách chọn)
Câu 6:
21/11/2024Trong khai triển nhị thức (x + 2y)5 có bao nhiêu số hạng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Lời giải
Trong khai triển nhị thức (a + b)n có n + 1 số hạng
Vậy trong khai triển nhị thức (x + 2y)5 có 5 + 1 = 6 số hạng
*Phương pháp giải:
Sử dụng công thức triển khai nhị thức
•
*Lý thuyết:
1. Nhị thức Newton là gì?
Nhị thức Newton là một định lý toán học quan trọng liên quan đến khai triển hàm mũ của tổng và phân tích các đa thức bậc cao. Định lý Nhị thức Newton có ứng dụng rộng rãi trong toán học và nhiều lĩnh vực khác, bao gồm:
+ Tính tổ hợp và chỉnh hợp: Định lý Nhị thức Newton là công cụ quan trọng trong việc tính toán số cách sắp xếp hoặc chọn k phần tử từ n phần tử mà không quan trọng thứ tự, điều này có ứng dụng trong nhiều vấn đề tổ hợp và chỉnh hợp.
+ Dãy số: Định lý Nhị thức Newton thường được sử dụng để chứng minh các thuộc tính của các dãy số, ví dụ như dãy số Fibonacci và dãy số Pascal.
+ Xác suất và thống kê: Trong xác suất và thống kê, định lý Nhị thức Newton được sử dụng để tính xác suất và biểu diễn các phân phối xác suất, nhất là trong việc tính toán xác suất của các biến ngẫu nhiên rời rạc.
+ Lý thuyết đồ thị: Công thức Nhị thức được sử dụng để tính toán số lượng đồ thị con trong một đồ thị, điều này có ứng dụng trong lý thuyết đồ thị và các vấn đề liên quan đến mạng lưới.
2. Công thức Nhị thức Newton và khai triển
Với là những số thực tùy ý và với mọi số tự nhiên , ta có:
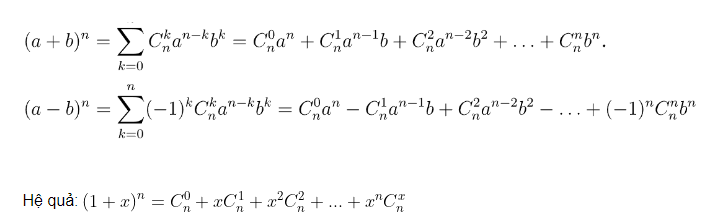
•
•
Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) ứng với n = 4 và n = 5.
Chú ý:
– Các hệ số trong khai triển nhị thức Newton (a + b)n với n = 0; 1; 2; 3; … được viết thành từng hàng và xếp thành bảng số như dưới đây.
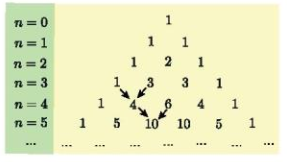
Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của 2 số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).
Bảng số trên dược gọi là tam giác Pascal (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 – 1662).
Xem thêm
Lý thuyết Nhị thức Newton (công thức, khai triển) các dạng bài tập và cách giải
Câu 7:
17/07/2024Lớp 10A có 20 học sinh nữ và 15 học sinh nam. Thầy giáo có bao nhiêu cách chọn ra một học sinh tham gia đội xung kích của trường
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Vì chọn ra một học sinh bất kỳ nên thầy giáo có thể chọn học sinh nam hoặc học sinh nữ.
Công đoạn 1, chọn học sinh nữ có 20 cách
Công đoạn 2, chọn học sinh nam có 15 cách
Tổng kết, áp dụng quy tắc cộng có 20 + 15 = 35 (cách chọn)
Câu 8:
10/12/2024Có bao nhiêu cách xếp 8 người ngồi vào một bàn tròn
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Lời giải
Vì xếp 8 người ngồi vào bàn tròn nên vị trí xếp người đầu tiên là như nhau có 1 cách xếp.
Xếp 7 người còn lại vào 7 vị trí nên có 7! cách xếp.
Tổng kết, xếp 8 người ngồi vào một bàn tròn có 1.7! = 7! (cách xếp)
*Phương pháp giải:
Cố định một bạn và xếp chỗ cho bạn còn lại.
- Sử dụng quy tắc nhân để tính số cách xếp.
*Lý thuyết:
Quy tắc nhân
– Giả sử một công việc được chia thành hai công đoạn. Công đoạn thứ nhất có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn thứ hai. Khi đó công việc có thể thực hiện theo m. n cách.
Quy tắc cộng
– Giả sử một công việc có thể được thực hiện theo phương án A hoặc B. Phương án A có m cách thực hiện, phương án B có n cách thực hiện không trùng với bất kì cách nào của phương án A. Khi đó, công việc có thể thực hiện theo m + n cách.
Xem thêm
Lý thuyết Quy tắc cộng và quy tắc nhân – Toán 10 Chân trời sáng tạo
Câu 9:
19/07/2024Trong một hộp có 7 viên bi đỏ, 5 viên bi trắng và 6 viên bi xanh. Chọn ngẫu nhiên ra 4 viên bi. Có bao nhiêu cách để chọn được số bi có đủ 3 màu và chọn được 2 viên bi xanh.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Vì chọn ngẫu nhiên 4 viên bi có đủ ba màu và có 2 bi xanh nên số bi phải chọn là: 2 viên bi xanh, 1 viên bi đỏ và 1 viên bi trắng.
Công đoạn 1, chọn 2 viên bi xanh trong 6 viên bi xanh có = 15 (cách chọn)
Công đoạn 2, chọn 1 viên bi đỏ trong 7 viên bi đỏ có 7 (cách chọn)
Công đoạn 3, chọn 1 viên bi trắng trong 5 viên bi trắng có 5 (cách chọn)
Vậy áp dụng quy tắc nhân số cách chọn ra 4 viên bi có đủ ba màu và có 2 bi xanh là: 15.7.5 = 525 (cách chọn).
Câu 10:
17/07/2024Một nhóm có 6 học sinh gồm 4 nam và 2 nữ. Hỏi có bao nhiêu cách chọn ra 3 học sinh trong đó có cả nam và nữ.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Vì chọn ra 3 học sinh có cả nam và nữ nên xảy ra các trường hợp sau:
Trường hợp ![]() , chọn
, chọn ![]() nam và 2 nữ
nam và 2 nữ
Công đoạn 1, chọn 1 nam trong 4 nam có 4 cách chọn;
Công đoạn 2, chọn 2 nữ trong 2 nữ có = 1 cách chọn;
Áp dụng quy tắc nhân trường hợp 1 có 4.1 = 4 cách chọn.
Trường hợp 2, chọn 2 nam và nữ có:
Công đoạn 1, chọn 2 nam trong 4 nam có = 6 cách chọn;
Công đoạn 2, chọn 1 nữ trong 2 nữ có 2 cách chọn;
Áp dụng quy tắc nhân trường hợp 2 có 6.2 = 12 cách chọn.
Áp dụng quy tắc cộng cả hai trường hợp có 4 + 12 = 16 (cách chọn).
Vậy có 16 cách chọn để 3 học sinh được chọn có cả nam và nữ.
Câu 13:
23/07/2024Trong các số nguyên từ 100 đến 999, số các số mà các chữ số của nó tăng dần hoặc giảm dần (kể từ trái qua phải) bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Vì các số tăng dần hoặc giảm dần nên số nguyên cần lập có 3 chữ số đôi một khác nhau. Xét hai trường hợp:
Trường hợp 1, Các chữ số tăng dần từ trái qua phải.
Khi đó 3 chữ số được chọn từ các số 1; 2; 3; 4; 5; 6; 7; 8; 9.
Với một cách chọn 3 chữ số từ tập này ta có duy nhất một cách xếp chúng theo thứ tự tăng dần. Do đó số các số lập được trong trường hợp này là: = 84 (số).
Trường hợp 2, Các chữ số giảm dần từ trái qua phải.
Khi đó 3 chữ số được chọn từ các số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
Với một cách chọn 3 chữ số từ tập này ta có duy nhất một cách xếp chúng theo thứ tự giảm dần. Do đó số các số lập được trong trường hợp này là: = 120 (số)
Tổng hợp, áp dụng quy tắc cộng số các số có thể lập là: 84 + 120 = 204 (số).
Câu 14:
15/07/2024Trong khai triển (x + 3)n+2 có 15 số hạng. Giá trị của n bằng
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Trong khai triển (a + b)n có n + 1 số hạng
Vì khai triển có 15 số hạng nên ta có n + 2 = 14. Vậy n = 12
Câu 15:
23/07/2024Từ 2 chữ số 1 và 8 lập được bao nhiêu số tự nhiên có 8 chữ số sao cho không có 2 chữ số 1 đứng cạnh nhau?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Vì lập số có 8 chữ số từ 2 số 1 và 8 sao cho không có 2 chữ số 1 đứng cạnh nhau nên ta có các trường hợp sau
+) Trường hợp 1. Có 8 chữ số 8 và không có chữ số 1. Do đó có 1 số.
+) Trường hợp 2. Có 1 chữ số 1 và 7 chữ số 8
Vì có 7 chữ số 8 nên tạo ra 8 khoảng trống nên có 8 cách xếp số 1. Do đó có 8 số.
+) Trường hợp 3. Có 2 chữ số 1 và 6 chữ số 8.
Xếp 6 số 8 ta có 1 cách. Từ 6 số 8 ta có có 7 chỗ trống để xếp 2 số 1 nên ta có: = 21 số.
+) Trường hợp 4. Có 3 chữ số 1 và 5 chữ số 8.
Tương tự trường hợp 3 từ 5 chữ số 8 ta có 6 chỗ trống để xếp 3 chữ số 1 nên ta có: = 20 số.
+) Trường hợp 5, Có 4 chữ số 1 và 4 chữ số 8.
Từ 4 chữ số 8 ta có 5 chỗ trống để xếp 4 chữ số 1 nên ta có: = 5 số.
Các trường hợp khác chắc chắn sẽ có hai chữ số 1 đứng cạnh nhau.
Tổng kết áp dụng quy tắc cộng ta có số các số có thể lập là : 1 + 8 + 21 + 20 + 5 = 55 số.
Câu 16:
18/07/2024Bạn An muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có 8 màu khác nhau, các cây bút chì cũng có 8 màu khác nhau. Như vậy bạn An có bao nhiêu cách chọn.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Việc bạn An mua một cây bút mực và một cây bút chì được chia làm hai công đoạn như sau:
Công đoạn 1, chọn cây bút mực: có 8 cách;
Công đoạn 2, chọn cây bút chì: có 8 cách.
Theo quy tắc nhân, số cách mua một cây bút mực và một cây bút chì là: 8.8 = 64 (cách ).
Câu 17:
14/07/2024Bạn Dũng có 8 quyển truyện tranh khác nhau và 7 quyển tiểu thuyết khác nhau. Bạn Dũng có bao nhiêu cách chọn ra một quyển sách để đọc vào cuối tuần.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Để bạn Dũng chọn một quyển sách để đọc vào cuối tuần có hai phương án sau:
Phương án 1. Quyển sách được chọn là truyện tranh, có 8 cách chọn.
Phương án 2. Quyển sách được chọn là tiểu thuyết, có 7 cách chọn.
Vậy theo quy tắc cộng, số cách bạn Dũng chọn một quyển sách để đọc vào cuối tuần là 8 + 7 = 15 (cách).
Câu 18:
21/07/2024Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Số các cách để chọn những màu cần dùng là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Mỗi cách chọn lần lượt 3 trong 5 màu để tô 3 nước khác nhau là một chỉnh hợp chập 3 của 5 phần tử.
Vậy số cách chọn là = 60 (cách).
Câu 19:
23/07/2024Cho các số 1; 2; 3; 4; 5; 6; 7. Có bao nhiêu số tự nhiên gồm 5 chữ số lấy từ 7 chữ số trên sao cho chữ số đầu tiên bằng chữ số 3
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Gọi số cần tìm có dạng: , a ≠ 0; a, b, c ∈ {1; 2; 3; 4; 5; 6; 7}.
Công đoạn 1. Chọn số a có 1 cách chọn ( vì chữ số bắt đầu bằng 3 nên a chỉ có 1 cách chọn là số 3).
Công đoạn 2. Chọn số b có 7 cách chọn (vì b chọn tuỳ ý nên b có thể chọn một trong 7 số 1; 2; 3; 4; 5; 6; 7).
Công đoạn 3. Chọn số c có 7 cách chọn (vì c chọn tuỳ ý nên c có thể chọn một trong 7 số 1; 2; 3; 4; 5; 6; 7).
Công đoạn 4. Chọn chữ số d có 7 cách chọn (vì d chọn tuỳ ý nên d có thể chọn một trong 7 số 1; 2; 3; 4; 5; 6; 7).
Công đoạn 5. Chọn chữ số e có 7 cách chọn (vì e chọn tuỳ ý nên e có thể chọn một trong 7 số 1; 2; 3; 4; 5; 6; 7).
Vậy số các số tự nhiên gồm 5 chữ số lấy từ 7 chữ số trên sao cho chữ số đầu tiên bằng 3 là: 1.7.7.7.7 = 2401 (số).
Câu 20:
04/11/2024Có bao nhiêu đoạn thẳng được tạo thành từ 10 điểm phân biệt khác nhau
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
*Lời giải:
Giả sử ta có 2 điểm A, B phân biệt thì có một đoạn thẳng AB (đoạn thẳng AB và đoạn thẳng BA là một)
Vì cứ chọn 2 điểm bất kỳ trong 10 điểm ta được một đoạn thẳng nên mỗi cách chọn ra 2 điểm trong 10 điểm là một tổ hợp chập 2 của 10 phần tử. Vậy số đoạn thẳng được tạo thành từ 10 điểm phân biệt khác nhau là = 45 (đoạn thẳng)
*Phương pháp giải:
- Chọn bất kì 2 điểm trong 10 điểm nên ta sẽ có là tổ hợp
- áp dụng công thức tổ hợp:
*Lý thuyến cần nắm về tổ hợp, chỉnh hợp:
Chỉnh hợp
Một chỉnh hợp chập k của n là một cách sắp xếp có thứ tự k phần tử từ một tập hợp n phần tử (với k, n là các số tự nhiên, 1 ≤ k ≤ n).
Số các chỉnh hợp chập k của n, kí hiệu là , được tính bằng công thức:
= n.(n – 1)…(n – k + 1) hay (1 ≤ k ≤ n).
Chú ý :
+ Hoán vị sắp xếp tất cả các phần tử của tập hợp, còn chỉnh hợp chọn ra một số phần tử và sắp xếp chúng.
+ Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử đó. Vì vậy Pn =
Tổ hợp
Một tổ hợp chập k của n là một cách chọn k phần tử từ một tập hợp n phần tử (với k, n là các số tự nhiên, 0 ≤ k ≤ n).
Số các tổ hợp chập k của n, kí hiệu là , được tính bằng công thức :
Chú ý :
+) <
+) Chỉnh hợp và tổ hợp có điểm giống nhau là đều chọn một số phần tử trong một tập hợp, nhưng khác nhau ở chỗ, chỉnh hợp là chọn có xếp thứ tự, còn tổ hợp là chọn không xếp thứ tự.
Ứng dụng hoán vị, chỉnh hợp, tổ hợp vào các bài toán đếm
Các khái niệm hoán vị, chỉnh hợp và tổ hợp liên quan mật thiết với nhau và là những khái niệm cốt lõi của các phép đếm. Rất nhiều bài toán liên quan đến việc lựa chọn, việc sắp xếp, vì vậy các công thức tính Pn, , sẽ được dùng rất nhiều.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - Toán 10 Kết nối tri thức
Giải Toán 10 (Kết nối tri thức): Bài tập cuối chương 8
TOP 30 câu Trắc nghiệm Ôn tập cuối chương 8 (Kết nối tri thức 2024) có đáp án - Toán 10
Câu 21:
22/07/2024Có bao nhiêu cách sắp xếp 3 nữ sinh và 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ đứng xen kẽ:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
- Trường hợp 1: nữ đứng trước
Có 6 vị trí để xếp, vì nam nữ đứng xen kẽ nên nữ sẽ đứng vị trí số 1, 3, 5 còn nam đứng vị trí số 2, 4, 6.
+ Sắp xếp học sinh nữ vào vị trí 1, 3, 5
Vị trí số 1 có 3 cách chọn (vì có thể chọn một bạn bất kỳ trong 3 bạn nữ).
Vị trí số 3 có 2 cách chọn (vì chỉ có thể chọn một trong hai bạn nữ còn lại).
Vị trí số 5 có 1 cách chọn (vì chỉ còn 1 bạn nữ để chọn).
+ Sắp xếp học sinh nam vào vị trí 2, 4, 6
Vị trí số 2 có 3 cách chọn (vì có thể chọn một bạn bất kỳ trong 3 bạn nam).
Vị trí số 4 có 2 cách chọn (vì chỉ có thể chọn một trong hai bạn nam còn lại).
Vị trí số 6 có 1 cách chọn (vì chỉ còn 1 bạn nam để chọn).
Suy ra , trường hợp 1 có 3.2.1.3.2.1 = 36 (cách xếp)
- Trường hợp 2, nam đứng trước
Tương tự như trường hợp 1, trường hợp 2 có 36 (cách xếp)
Vậy áp dụng quy tắc cộng ta có cả hai trường hợp có 36 + 36 = 72 (cách xếp).
B đúng.
* Quy tắc nhân
- Quy tắc nhân: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.
- Chú ý: Quy tắc nhân có thể mở rộng cho nhiều hành động liên liếp.
- Ví dụ 3. Cho tập A = {1; 3; 4; 5; 6}. Hỏi lập được bao nhiêu số tự nhiên có 2 chữ số đôi một khác nhau từ tập A?
Lời giải:
Để tạo ra một số tự nhiên có 2 chữ số đôi một khác nhau từ tập A, ta phải thực hiện liên tiếp hai hành động:
- Hành động 1: Chọn chữ số hàng chục có 5 cách.
- Hành động 2. Chọn chữ số hàng đơn vị. Ứng với mỗi cách chọn chữ số hàng chục, ta có 4 cách chọn chữ số hàng đơn vị (vì chữ số hàng chục khác chữ số hàng đơn vị).
Theo quy tắc nhân, số các số tự nhiên thỏa mãn đầu bài là: 5.4 = 20 số.
- Ví dụ 4. Một người vào cửa hàng ăn, người đó chọn thực đơn gồm 1 món ăn trong 10 món, 1 loại quả tráng miệng trong 6 loại quả tráng miệng và 1 nước uống giải khát trong 4 loại nước uống. Hỏi có bao nhiêu cách chọn thực đơn?
Lời giải:
Để chọn một thực đơn, ta cần thực hiện liên tiếp ba hành động:
- Chọn 1 món ăn trong 10 món có 10 cách.
- Chọn 1 loại quả tráng miệng trong 6 loại quả tráng miệng có 6 cách.
- Chọn 1 nước uống trong 4 loại nước uống có 4 cách.
Theo quy tắc nhân, số cách cách chọn thực đơn là 10.6.4 = 240 cách.
* Quy tắc cộng
- Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m + n cách thực hiện.
- Quy tắc cộng được phát biểu ở trên thực chất là quy tắc đếm số phần tử của hợp hai tập hợp hữu hạn không giao nhau, được phát biểu như sau:
Nếu A và B là các tập hợp hữu hạn và không giao nhau thì:
- Chú ý: Quy tắc cộng có thể mở rộng cho nhiều hành động.
- Ví dụ 1. Một lớp học có 21 bạn nữ và 19 bạn nam. Giáo viên chủ nhiệm cần chọn một bạn để làm lớp trưởng. Hỏi giáo viên có bao nhiêu cách chọn?
Lời giải:
+ Trường hợp 1. Giáo viên chọn 1 bạn nam: có 19 cách.
+ Trường hợp 2. Giáo viên chọn 1 bạn nữ: có 21 cách
Theo quy tắc cộng, giáo viên sẽ có: 19 + 21 = 40 cách chọn 1 bạn làm lớp trưởng.
- Ví dụ 2. Bạn Lan có 10 quyển sách khác nhau; 12 chiếc bút khác nhau và 5 cục tẩy khác nhau. Bạn Lan cần chọn một món đồ để đem tặng Hoa. Hỏi bạn Lan có bao nhiêu cách chọn?
Lời giải:
Bạn Lan có thể chọn:
+ Một quyển sách: có 10 cách chọn
+ Một chiếc bút: có 12 cách chọn.
+ Một cục tẩy: có 5 cách chọn.
Theo quy tắc cộng, bạn Lan có: 10 + 12 + 5 = 27 cách chọn.
Xem thêm một số tài liệu liên quan hay, chi tiết khác:
Câu 22:
21/07/2024Một hội đồng gồm 2 giáo viên và 3 học sinh được chọn từ một nhóm 5 giáo viên và 6 học sinh. Hỏi có bao nhiêu cách chọn?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Công đoạn 1, chọn giáo viên
Mỗi cách chọn 2 giáo viên trong 5 giáo viên là một tổ hợp chập 2 của 5 phần tử. Vậy số cách chọn ra 2 giáo viên là: = 10.
Công đoạn 2, chọn học sinh
Mỗi cách chọn 3 học sinh trong 6 học sinh là một tổ hợp chập 3 của 6 phần tử. Vậy số cách chọn ra 3 học sinh là: = 20
Tổng kết, áp dụng quy tắc nhân số cách chọn một hội đồng gồm 2 giáo viên và 3 học sinh là: 10.20 = 200 (cách)
Câu 23:
18/07/2024Có bao nhiêu cách xếp 5 người thành một hàng dọc
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Mỗi cách xếp 5 người thành một hàng dọc là một hoán vị của 5 người đó. Vậy số cách xếp 5 người thành một hàng dọc là: 5! = 120.
Câu 24:
21/07/2024Có bao nhiêu số tự nhiên gồm 5 chữ số chia hết cho 10
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Gọi số cần tìm có dạng : , a ≠ 0
Công đoạn 1, chọn số e có 1 cách chọn (vì số chia hết cho 10 nên e chỉ có thể chọn là số 0)
Công đoạn 2, chọn số a có 9 cách chọn (vì a ≠ 0 nên a chỉ được chọn một trong 9 số 1; 2; 3 ; 4; 5; 6; 7; 8; 9)
Công đoạn 3, chọn số b có 10 cách chọn (vì b chọn tuỳ ý nên b có thể chọn 1 trong 10 số 0; 1; 2; 3 ; 4; 5; 6; 7; 8; 9)
Công đoạn 4, chọn số c có 10 cách chọn (vì c chọn tuỳ ý nên c có thể chọn 1 trong 10 số 0; 1; 2; 3 ; 4; 5; 6; 7; 8; 9)
Công đoạn 5, chọn số d có 10 cách chọn (vì d chọn tuỳ ý nên d có thể chọn 1 trong 10 số 0; 1; 2; 3 ; 4; 5; 6; 7; 8; 9)
Tổng kết, theo quy tắc nhân ta có Số các số tự nhiên gồm 5 chữ số chia hết cho 10 là: 1.9.10.10.10 = 9000 (số).
Câu 25:
15/07/2024Tên 15 học sinh được ghi vào 15 tờ giấy để vào trong hộp. Có bao nhiêu cách chọn tên 4 học sinh để cho đi du lịch
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Mỗi cách chọn ra 4 học sinh trong 15 học sinh là một tổ hợp chập 4 của 15 phần tử. Vậy số cách chọn ra 4 học sinh là: = 1365 (cách).
Câu 26:
22/07/2024Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài sao cho sách Văn phải xếp kề nhau và sách Toán xếp kề nhau?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có số cách xếp sách văn là 5! cách xếp
Số cách xếp sách Toán là 7! cách xếp
Trường hợp 1, sách Văn đứng trước sách Toán ta có số cách xếp là 5!.7! cách xếp
Trường hợp 2, sách Toán đứng trước sách Văn ta có số cách xếp là 7!.5! cách xếp
Tổng kết, áp dụng quy tắc cộng ta có số cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài sao cho sách Văn phải xếp kề nhau và sách Toán xếp kề nhau là 5!.7! + 7!.5! = 2.5!.7!
Câu 27:
21/07/2024Khai triển nhị thức (2x + y)5 ta được kết quả là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Khai triển nhị thức
(2x + y)5 = (2x)5(y)0 + (2x)4(y)1 + (2x)3(y)2 + (2x)2(y)3 + (2x)(y)4 + (2x)0(y)5 = 32x5 + 80x4y + 80x3y2 + 40x2y3 + 10xy4 + y5 .
Câu 29:
23/07/2024Trong khai triển (3x – y)7 số hạng chứa x4y3 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là an – k .bk (k ≤ n)
Thay a = 3x, b = - y vào trong công thức ta có
(3x)7 – k .(- y)k = (- 1)k(3x)7 – k .(y)k
Số hạng cần tìm chứa x4y3 nên ta có x7 – kyk = x4y3
Vậy k = 3 thoả mãn bài toán
Khi đó hệ số cần tìm là (- 1)3(3)7 – 3x4 y3 = - 2835x4 y3
Câu 30:
22/07/2024Trong khai triển (2x – 1)10 hệ số của số hạng chứa x8 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là an – k .bk (k ≤ n)
Thay a = 2x, b = - 1 vào trong công thức ta có
(2x)10 – k .(- 1)k = (-1)k(2)10-k(x)10 – k
Số hạng cần tìm chứa x8 nên ta có 10 – k = 8
Vậy k = 2 thoả mãn bài toán
Khi đó hệ số cần tìm là (- 1)2(2)8 = 11520.
Có thể bạn quan tâm
- Thi Online Trắc nghiệm Toán 10 Bài tập cuối chương 8 có đáp án (372 lượt thi)
- Thi Online Trắc nghiệm Toán 10 KNTT Bài ôn tập cuối chương 8 (Phần 2) có đáp án (604 lượt thi)
Các bài thi hot trong chương
- Thi Online Trắc nghiệm Toán 10 KNTT Bài 25. Nhị thức Newton (Phần 2) có đáp án (755 lượt thi)
- Thi Online Trắc nghiệm Toán 10 KNTT Bài 24. Hoán vị, tổ hợp, chỉnh hợp (Phần 2) có đáp án (753 lượt thi)
- Thi Online Trắc nghiệm Toán 10 KNTT Bài 23. Quy tắc đếm (Phần 2) có đáp án (672 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 24. Hoán vị, chỉnh hợp và tổ hợp có đáp án (494 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 25. Nhi thức Newton có đáp án (493 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 23. Quy tắc đếm có đáp án (395 lượt thi)