Thi Online Trắc nghiệm Toán 10 Bài 17. Dấu của tam thức bậc hai có đáp án
Trắc nghiệm Toán 10 Bài 17. Dấu của tam thức bậc hai có đáp án
-
343 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x) = x2 + 12x + 36 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét phương trình f(x) = x2 + 12x + 36 = 0 \( \Leftrightarrow \)x = – 6 và a = 1 > 0.
Ta có bảng xét dấu

Đáp án đúng là C
Câu 2:
17/11/2024Tam thức y = x2 – 12x – 13 nhận giá trị âm khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Lời giải
Xét x2 – 12x – 13 =0 \[ \Leftrightarrow \left[ \begin{array}{l}x = 13\\x = - 1\end{array} \right.\]
Ta có bảng xét dấu

Dựa vào bảng xét dấu ta có tam thức y = x2 – 12x – 13 nhận giá trị âm khi
– 1 < x < 13.
*Phương pháp giải:
Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0).
+ Nếu ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ℝ.
+ Nếu ∆ = 0 thì f(x) cùng dấu với hệ số a với mọi và
+ Nếu ∆ > 0 thì tam thức f(x) có hai nghiệm phân biệt x1 và x2 (x1 < x2). Khi đó, f(x) cùng dấu với hệ số a với mọi x ∈ (–∞; x1) ∪ (x2; +∞); f(x) trái dấu với hệ số a với mọi x ∈ (x1; x2).
Tức là, khi ∆ > 0, dấu của f(x) và a là: “Trong trái, ngoài cùng”
*Lý thuyết:
1. Dấu của tam thức bậc hai
Tam thức bậc hai (đối với x) là biểu thức có dạng ax2 + bx + c, trong đó a, b, c là những số thực cho trước (với a ≠ 0), được gọi là các hệ số của tam thức bậc hai.
Chú ý : Nghiệm của phương trình bậc hai ax2 + bx + c = 0 cũng là nghiệm của tam thức bậc hai ax2 + bx + c.
Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0).
+ Nếu ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ℝ.
+ Nếu ∆ = 0 thì f(x) cùng dấu với hệ số a với mọi và
+ Nếu ∆ > 0 thì tam thức f(x) có hai nghiệm phân biệt x1 và x2 (x1 < x2). Khi đó, f(x) cùng dấu với hệ số a với mọi x ∈ (–∞; x1) ∪ (x2; +∞); f(x) trái dấu với hệ số a với mọi x ∈ (x1; x2).
Tức là, khi ∆ > 0, dấu của f(x) và a là: “Trong trái, ngoài cùng”
Xem thêm
Lý thuyết Dấu của tam thức bậc hai - Toán 10 Kết nối tri thức
Câu 3:
12/07/2024Tam thức nào sau đây nhận giá trị âm với mọi x < 2
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét đáp án A: y = x2 – 5x +6
Xét x2 – 5x +6 = 0 \[ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 2\end{array} \right.\]
Ta có bảng xét dấu

Dựa vào bảng xét dấu ta có tam thức y = x2 – 5x + 6 nhận giá trị âm khi 2 < x < 3.
Vậy đáp án A sai.
Xét đáp án B: y = 16 – x2
Xét 16 – x2 = 0 \[ \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\]
Ta có bảng xét dấu

Dựa vào bảng xét dấu ta có tam thức y = 16 – x2 xét trên khoảng (– ∞; 2) nhận giá trị âm khi trên khoảng (– ∞; – 4) nhận giá trị dương trên khoảng (– 4; 2).
Vậy đáp án B sai.
Xét đáp án C: y = x2 – 2x + 3
Xét x2 – 2x + 3 = 0 \[ \Leftrightarrow \]Phương trình vô nghiệm
Ta có bảng xét dấu

Dựa vào bảng xét dấu ta có tam thức y = x2 – 2x + 3 nhận giá trị dương với mọi x \[ \in \]ℝ
Vậy đáp án C sai.
Xét đáp án D: y = – x2 + 5x – 6.
Xét – x2 + 5x – 6 = 0 \[ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 3\end{array} \right.\]
Ta có bảng xét dấu

Dựa vào bảng xét dấu ta có tam thức y = – x2 + 5x – 6 nhận giá trị âm khi \[x \in ( - \infty ;2) \cup (3; + \infty )\]
Vậy đáp án D đúng.
Câu 4:
12/07/2024Phương trình x2 – 2(m – 1)x + m – 3 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
x2 – 2(m – 1)x + m – 3 = 0 có 2 nghiệm đối nhau khi \(\left\{ \begin{array}{l}\Delta ' > 0\\S = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m + 4 > 0\\m - 1 = 0\end{array} \right.\).
Xét biểu thức m2 – 3m + 4 = \[{\left( {m - \frac{3}{2}} \right)^2}\] + \[\frac{7}{4}\] > 0 với mọi m
Vậy phương trình có 2 nghiệm đối dấu khi m = 1.
Đáp án đúng là C.
Câu 5:
23/07/2024Phương trình x2 + x + m = 0 vô nghiệm khi và chỉ khi:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
x2 + x + m = 0 vô nghiệm khi ∆ < 0
Ta có ∆ = 12 – 4.1.m < 0 \( \Leftrightarrow m > \frac{1}{4}\).
Vậy đáp án đúng là C.
Câu 6:
15/07/2024Các giá trị m làm cho biểu thức f(x) = x2 + 4x + m – 5 luôn dương là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: f(x) = x2 + 4x + m – 5 luôn luôn dương \[ \Leftrightarrow \] x2 + 4x + m – 5 > 0 với mọi x \[ \in \]ℝ
\[ \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\\Delta ' = {2^2} - (m - 5) < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\m > 9\end{array} \right.\].
Vậy đáp án đúng là C.
Câu 7:
23/07/2024Cho hàm số f(x) = mx2 – 2mx + m + 1. Giá trị của m để f(x) > 0, \(\forall x \in \mathbb{R}\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
TH1. m = 0. Khi đó: f(x) = 1 > 0\(\forall x \in \mathbb{R}\).
TH2. m ≠ 0. Khi đó:
f(x) = mx2 – 2mx + m + 1 > 0 \(\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}a = m > 0\\\Delta ' = {m^2} - m\left( {m + 1} \right) < 0\end{array} \right.\).\( \Leftrightarrow \left\{ \begin{array}{l}a = m > 0\\m > 0\end{array} \right. \Leftrightarrow m > 0\)
Vậy m ≥ 0 thỏa mãn bài toán.
Câu 8:
12/07/2024Tập nghiệm của bất phương trình x2 + 4x + 4 > 0 là:
 Xem đáp án
Xem đáp án
Chọn C
Xét x2 + 4x + 4 = 0 \[ \Leftrightarrow \] x = – 2.
Ta có bảng xét dấu

Dựa vào bảng xét dấu tập nghiệm của bất phương trình là \(( - \infty ; - 2) \cup ( - 2; + \infty )\).
Câu 9:
15/11/2024Tìm tập xác định của hàm số \(y = \sqrt {2{x^2} - 5x + 2} \).
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Lời giải
Hàm số \(y = \sqrt {2{x^2} - 5x + 2} \) xác định khi và chỉ khi 2x2 – 5x + 2 ≥ 0
Xét 2x2 – 5x + 2 = 0 \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{2}\\x = 2\end{array} \right.\)
Ta có bảng xét dấu
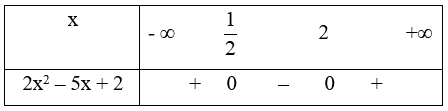
Từ bảng xét dấu ta có 2x2 – 5x + 2 ≥ 0 \(x \in \left( { - \infty ;\frac{1}{2}} \right] \cup \left[ {2; + \infty } \right)\)
Vậy đáp án đúng là C.
*Phương pháp giải:
Biểu thức trong căn lớn hơn hoặc bằng 0
Giải bất phương trình bằng 0 so sánh rồi kết luận
*Lý thuyết:
Cho số thực dương a khác 1.
Hàm số y = ax được gọi là hàm số mũ cơ số a.
Ví dụ 1. Các hàm số y = 2x; là các hàm số mũ.
2. Đạo hàm của hàm số mũ
Ta thừa nhận công thức:
– Định lí 1: Hàm số y = ex có đạo hàm tại mọi x và (ex)’ = ex.
– Chú ý: Công thức đạo hàm của hàm hợp đối với hàm số eu ( với u = u(x))
là (eu)’ = u’. eu.
– Định lí 2: Hàm số y = ax ( a > 0; a ≠ 1) có đạo hàm tại mọi
Xem thêm
Lý thuyết Hàm số mũ. Hàm số logarit (năm 2024 + Bài Tập)– Toán 12
Câu 10:
18/07/2024Tập ngiệm của bất phương trình: x(x + 5) ≤ 2(x2 + 2) là:
 Xem đáp án
Xem đáp án
Đáp án đúng: A
Ta có: x(x + 5) ≤ 2(x2 + 2) \( \Leftrightarrow \)x2 – 5x + 4 ≥ 0
Đặt f(x) = x2 – 5x + 4 ta có f(x) = 0 \( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\).
Ta có bảng xét dấu :

Dựa vào bảng xét dấu nghiệm của bất phương trình \[x \in (--\infty ;1] \cup [4; + \infty )\]
Câu 11:
17/07/2024Bất phương trình: \[\left( {{x^2} - 3x - 4} \right).\sqrt {{x^2} - 5} < 0\] có bao nhiêu nghiệm nguyên dương?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có điều kiện: x2 – 5 ≥ 0\[ \Leftrightarrow \left[ \begin{array}{l}x \le - \sqrt 5 \,\\x \ge \sqrt 5 \end{array} \right.\].
Vậy \[\left( {{x^2} - 3x - 4} \right).\sqrt {{x^2} - 5} < 0\]\[ \Leftrightarrow \] x2 – 3x – 4 < 0.
Xét x2 – 3x – 4 = 0 \[ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 4\end{array} \right.\]
Ta có bảng xét dấu
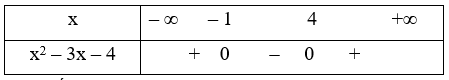
Dựa vào bảng xét dấu ta có x2 – 3x – 4 < 0 \[ \Leftrightarrow \] – 1 < x < 4
Kết hợp với điều kiện ta được: \[x \in \left( {\sqrt 5 ;4} \right)\]. Suy ra nghiệm nguyên dương của bất phương trình đã cho là: x = 3.
Vậy bất phương trình có 1 nghiệm nguyên dương.
Câu 12:
12/07/2024Tìm tất cả các giá trị của a để bất phương trình ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\) \( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta = {\left( { - 1} \right)^2} - 4.a.a \le 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\1 - 4{a^2} \le 0\end{array} \right.\)
Xét tam thức bậc hai f(a) = 1 – a2, có ∆ = 02 – 4.(-4).1 = 16 > 0. Do đó f(a) có hai nghiệm phân biệt \(a = \frac{1}{2}\) và \(a = - \frac{1}{2}\)
Ta có bảng xét dấu
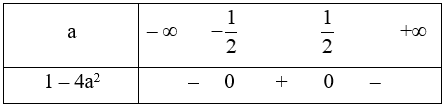
Dựa vào bảng xét dấu ta có 1 – 4a2 ≤ 0 \( \Leftrightarrow a \in \left( { - \infty ; - \frac{1}{2}} \right] \cup \left[ {\frac{1}{2}; + \infty } \right)\).
Kết hợp với điều kiện a > 0 suy ra a ∈ \(\left[ {\frac{1}{2}; + \infty } \right)\).
Vậy để ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\) thì a ∈ \(\left[ {\frac{1}{2}; + \infty } \right)\) hay a ≥ \(\frac{1}{2}\).
Câu 13:
15/07/2024Để f(x) = x2 + (m + 1)x +2m + 7 > 0 với mọi x thì
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có f(x) > 0 với
Xét tam thức bậc hai f(m) = m2 – 6m – 27, có ∆’ = 9 – (-27) = 36 > 0. Do đó f(m) có hai nghiệm phân biệt là m = -3 và m = 9.
Ta có bảng xét dấu

Dựa vào bảng xét dấu để ∆ < 0 thì – 3 < m < 9.
Vậy đáp án đúng là C.
Câu 14:
21/07/2024Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có f(x) > 0 vô nghiệm \( \Leftrightarrow f\left( x \right) \le 0\,\,\forall x \in \mathbb{R}\).
Xét m = 3 ta có f(x) = 5x – 4 với \(x > \frac{4}{5}\) thì f(x) > 0 nên m = 3 không thỏa mãn.
Xét m ≠ 3 ta có \(f\left( x \right) \le 0\,\,\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}a = m - 3 < 0\\\Delta = {m^2} + 20m - 44 \le 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m < 3\\{m^2} + 20m - 44 \le 0\end{array} \right.\)
Xét tam thức bậc hai (biến m): m2 + 20m – 44 có ∆’ = 102 – (-44) = 144 > 0. Do đó tam thức có hai nghiệm phân biệt x = -22 và x = 2.
Ta có bảng xét dấu

Để \(f\left( x \right) \le 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}m < 3\\ - 22 \le m \le 2\end{array} \right. \Leftrightarrow - 22 \le m \le 2\)
Vậy đáp án đúng là B.
Câu 15:
18/07/2024Cho bất phương trình 2x2 – 4x + m + 5 > 0. Tìm m để bất phương trình đúng \(\forall x \ge 3\)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: a = 2 > 0. Do đó, 2x2 – 4x + m + 5 > 0, \(\forall x \ge 3\) sẽ có trường hợp sau:
Trường hợp 1. ∆ < 0 \( \Leftrightarrow \) (– 4)2 – 4.2.(m + 5) < 0 \( \Leftrightarrow \) m > – 3, khi đó
2x2 – 4x + m + 5 > 0 với \(\forall x \in \mathbb{R}\).
Do đó 2x2 – 4x + m + 5 > 0 với \(\forall x \ge 3\).
Trường hợp 2. ∆ ≥ 0, khi đó phương trình 2x2 – 4x + m + 5 = 0 sẽ có hai nghiệm x1; x2.
Do đó, để 2x2 – 4x + m + 5 > 0, \(\forall x \ge 3\)\[ \Leftrightarrow \left\{ \begin{array}{l}\Delta \ge 0\\{x_1} \le {x_2} < 3\end{array} \right.\]
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta \ge 0\\a\,f\left( 3 \right) > 0\\\frac{S}{2} < 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \le - 3\\2\left( {{{2.3}^2} - 4.3 + m + 5} \right) > 0\\1 < 3\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \le - 3\\m > - 11\end{array} \right.\)\( \Leftrightarrow \). – 11 < m ≤ – 3
Kết hợp hai trường hợp lại ta được m > – 11 thì thì 2x2 – 4x + m + 5 > 0 với \(\forall x \ge 3\).
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài 17. Dấu của tam thức bậc hai có đáp án (278 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 17. Dấu của tam thức bậc hai có đáp án (342 lượt thi)
Các bài thi hot trong chương
- Thi Online Trắc nghiệm Toán 10 Bài 16. Hàm số bậc hai có đáp án (462 lượt thi)
- Trắc nghiệm Toán lớp 10 Bài 16. Hàm số bậc hai có đáp án (424 lượt thi)
- Trắc nghiệm Toán 10 Bài 15. Hàm số có đáp án (411 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 15. Hàm số có đáp án (311 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 18. Phương trình quy về phương trình bậc hai có đáp án (281 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài tập cuối chương 6 có đáp án (255 lượt thi)
- Trắc nghiệm Toán 10 Bài tập cuối chương 6 có đáp án (253 lượt thi)
- Trắc nghiệm Toán 10 Bài 18. Phương trình quy về phương trình bậc hai có đáp án (235 lượt thi)

