30 câu hỏi trắc nghiệm thuộc Bài tập Lượng giác từ đề thi Đại học cơ bản, nâng cao (P1) (Đề số 3)

Câu 1:

17/07/2024

Cho phương trình $\cos x + \cos \frac{x}{2} + 1 = 0$ . Nếu đặt $t = \cos \frac{x}{2}$ , ta được phương trình nào sau đây?

Xem đáp án

Câu 2:

17/07/2024

Tìm tất cả các giá trị thực của tham số m để phương trình $\cos 2 x - (2 m + 1) \cos x + m + 1 = 0$ có nghiệm trên khoảng $(\frac{π}{2}; \frac{3 π}{2})$

Xem đáp án

Câu 3:

17/07/2024

Trong các hàm số sau, hàm nào là hàm số chẵn?

Xem đáp án

Câu 4:

17/07/2024

Đạo hàm của hàm số $y = x . \sin x$ bằng

Xem đáp án

Câu 5:

17/07/2024

Nghiệm của phương trình $\sin (x + \frac{π}{3}) = 0$

Xem đáp án

Vậy nghiệm của phương trình là $x = - \frac{π}{3} + k π, k \in ℤ$ .

Câu 6:

17/07/2024

Trong các khẳng định sau khẳng định nào sai?

A. Hàm số y=cosx đồng biến trên tập xác định.

B. Hàm số y=cosx là hàm số tuần hoàn chu kì $2 π$ .

C. Hàm số y=cosx có đồ thị là đường hình sin.

D. Hàm số y=cosx là hàm số chẵn.

Xem đáp án

Câu 7:

10/11/2024

Nghiệm của phương trình sin2x+cosx=0 là

Xem đáp án

Đáp án đúng là B

Lời giải

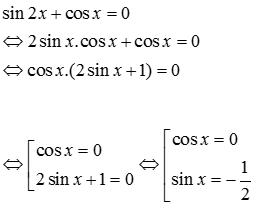
*Phương pháp giải:

Phương trình sinx = sinα; với α là một số cho trước, có các nghiệm là:

$x = α + k 2 π$ và $x = π - α + k 2 π; k \in ℤ$

*Lý thuyết:

Phương trình sinx = a.

Xét phương trình sinx = a (1)

- Trường hợp |a| > 1

Phương trình (1) vô nghiệm vì |sinx| ≤ 1 với mọi x.

- Trường hợp |a| ≤ 1

Gọi α là số đo bằng radian của một cung lượng giác. Khi đó, phương trình sinx = a có các nghiệm là:

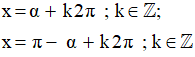
Nếu số thực α thỏa mãn điều kiện: $\{\begin{matrix} \frac{- π}{2} \leq α \leq \frac{π}{2} \\ \sin α = a \end{matrix}$ thì ta viết α = arcsina (đọc là ac-sin-a; nghĩa là cung có sin bằng a). Khi đó, các nghiệm của phương trình sinx = a được viết là:

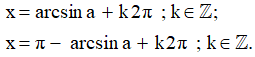
- Chú ý:

a) Phương trình sinx = sinα; với α là một số cho trước, có các nghiệm là:

$x = α + k 2 π$ và $x = π - α + k 2 π; k \in ℤ$

Tổng quát:

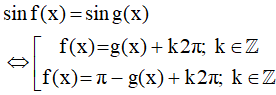
b) Phương trình sinx = sinβ⁰ có các nghiệm là:

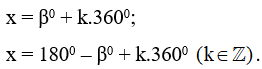
c) Trong một công thức về nghiệm của phương trình lương giác không được dùng đồng thời hai đơn vị độ và radian.

d) Các trường hợp đặc biệt:

+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là $x = \frac{π}{2} + k 2 π; k \in ℤ$ .

+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là $x = - \frac{π}{2} + k 2 π; k \in ℤ$ .

+ Khi a = 0: Phương trình sinx = 0 có các nghiệm là $x = k π; k \in ℤ$ .

Xem thêm

Lý thuyết Phương trình lượng giác cơ bản (mới + Bài Tập) – Toán 11

TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án ) – Toán 11

Câu 8:

17/07/2024

Nghiệm phương trình $\sin x + \sqrt{3} \cos x = 1$ là

Xem đáp án

Câu 9:

17/07/2024

Cho biểu thức $P = x^{- \frac{3}{4}} \sqrt{\sqrt{x^{5}}}$ , $x > 0$ . Khẳng định nào sau đây là đúng?

A. $x^{- 2}$

B. $x^{- \frac{1}{2}}$

C. $x^{\frac{1}{2}}$

D. $x^{2}$

Xem đáp án

Câu 10:

19/07/2024

Cho cấp số cộng $(u_{n})$ với số hạng đầu tiên $u_{1} = 2$ và công sai $d = 2$ . Tìm $u_{2018}$

A. $2^{2018}$

B. $2^{2017}$

C. 4036

D. 4038

Xem đáp án

Câu 11:

17/07/2024

Viết công thức tính thể tích của khối lăng trụ có diện tích đáy là B (đvdt) và chiều cao có độ dài là h.

A. V= $B^{2}$ h

B. V=Bh

C. V= $\frac{1}{3}$ Bh

D. V=3Bh

Xem đáp án

Đáp án B

Câu 12:

17/07/2024

Tập xác định của hàm số $y = \tan 2 x$ là:

Xem đáp án

Câu 13:

18/07/2024

Tập xác định của hàm số $y = \frac{1}{\sqrt{\sin x + 1}}$ là

Xem đáp án

Câu 14:

17/07/2024

Nghiệm âm lớn nhất của phương trình $\frac{\sqrt{3}}{\sin^{2} x} = 3 c o t x + \sqrt{3}$

A. $- \frac{π}{6}$

B. $- \frac{5 π}{6}$

C. $- \frac{π}{2}$

D. $- \frac{2 π}{3}$

Xem đáp án

Câu 15:

17/07/2024

Nghiệm của phương trình lượng giác $\cos^{2} x - \cos x = 0$ thỏa mãn điều kiện $0 < x < π$ là

A. 0

B. $\frac{3 π}{4}$

C. $\frac{π}{2}$

D. $- \frac{π}{2}$

Xem đáp án

Câu 16:

17/07/2024

Tất cả các nghiệm của phương trình tanx=cotx là

Xem đáp án

Câu 17:

17/07/2024

Số nghiệm của phương trình $\sin 5 x + \sqrt{3} \cos 5 x = 2 \sin 7 x$ trên khoảng $(0; \frac{π}{2})$ là

A. 4

B. 1

C. 3

D. 2

Xem đáp án

Vậy phương trình có tất cả là 4 nghiệm.

Câu 18:

17/07/2024

Tập xác định D của hàm số $y = \frac{2017}{\sin x}$ là

Xem đáp án

Câu 19:

25/11/2024

Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất phương trình $\sin (3 x - \frac{π}{4}) = \frac{\sqrt{3}}{2}$ bằng

A. $\frac{π}{9}$

B. $\frac{π}{6}$

C. $- \frac{π}{6}$

D. $- \frac{π}{9}$

Xem đáp án

Đáp án đúng: C

*Lời giải:

*Phương pháp giải:

- Áp dụng phương trình lượng giác cơ bản để giải bài toán tìm nghiệm

*Lý thuyết nắm thêm về phương trình lượng giác:

1. Phương trình sinx = a.

Xét phương trình sinx = a (1)

- Trường hợp |a| > 1

Phương trình (1) vô nghiệm vì |sinx| ≤ 1 với mọi x.

- Trường hợp |a| ≤ 1

Gọi α là số đo bằng radian của một cung lượng giác. Khi đó, phương trình sinx = a có các nghiệm là:

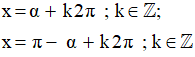
Nếu số thực α thỏa mãn điều kiện: $\{\begin{matrix} \frac{- π}{2} \leq α \leq \frac{π}{2} \\ \sin α = a \end{matrix}$ thì ta viết α = arcsina (đọc là ac-sin-a; nghĩa là cung có sin bằng a). Khi đó, các nghiệm của phương trình sinx = a được viết là:

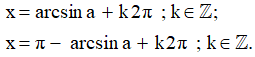
- Chú ý:

a) Phương trình sinx = sinα; với α là một số cho trước, có các nghiệm là:

$x = α + k 2 π$ và $x = π - α + k 2 π; k \in ℤ$

Tổng quát:

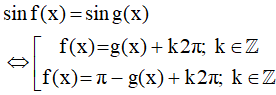
b) Phương trình sinx = sinβ0 có các nghiệm là:

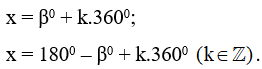
c) Trong một công thức về nghiệm của phương trình lương giác không được dùng đồng thời hai đơn vị độ và radian.

d) Các trường hợp đặc biệt:

+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là $x = \frac{π}{2} + k 2 π; k \in ℤ$ .

+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là $x = - \frac{π}{2} + k 2 π; k \in ℤ$ .

+ Khi a = 0: Phương trình sinx = 0 có các nghiệm là $x = k π; k \in ℤ$ .

2. Phương trình cosx = a.

- Trường hợp |a| > 1

Phương trình cosx = a vô nghiệm vì $|cosx| \leq 1$ với mọi x.

- Trường hợp $|a| \leq 1$ .

Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là: $x = \pm α + k 2 π; k \in ℤ$

- Chú ý:

a) Phương trình cosx = cosα, với α là một số cho trước, có các nghiệm là: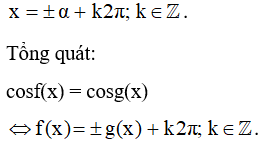

b) Phương trình cos x= cosβ0 có các nghiệm là $x = \pm β^{0} + k 360^{0}; k \in ℤ$

c) Nếu số thực α thỏa mãn điều kiện: $\{\begin{matrix} 0 \leq α \leq π \\ \cos α = a \end{matrix}$ thì ta viết α = arccosa (đọc là ac – cosin- a, có nghĩa là cung có cosin bằng a). Khi đó, các nghiệm của phương trình cos x = a còn được viết là: