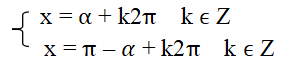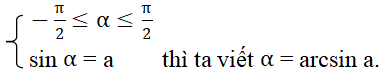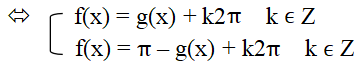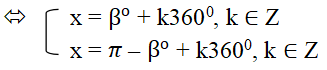Bài tập Lượng giác từ đề thi Đại học cơ bản, nâng cao (P1)
Bài tập Lượng giác từ đề thi Đại học cơ bản, nâng cao (P1) (Đề số 2)
-
1067 lượt thi
-
30 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 17:
21/07/2024Phương trình cosx=cosπ3 có tất cả các nghiệm là:
 Xem đáp án
Xem đáp án
Xét phương trình: cosx=cosπ3
⇔x=±π3+k2π,k∈ℤ
Vậy nghiệm của phương trình là: x=±π3+k2π,k∈ℤ.
Chọn C
Câu 21:
12/11/2024Cho phương trình sin(2x-π4)=sin(x+3π4). Tính tổng các nghiệm thuộc khoảng (0;π) của phương trình trên.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Lời giải
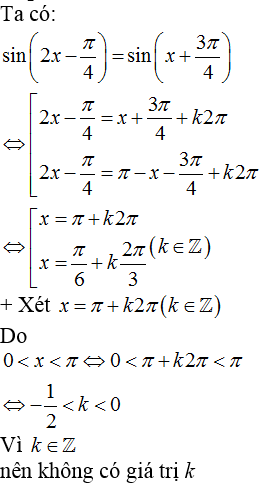
*Phương pháp giải:
Sử dụng phương trình sin
Xét hai trường hợp để tìm k
Kết luận
*Lý thuyết:
. Phương trình sin x = a (1)
- Trường hợp |a| > 1: Phương trình (1) vô nghiệm
- Trường hợp |a| ≤ 1: Phương trình (1) có các nghiệm là
+ Nếu số thực α thoả mãn điều kiện
- Lưu ý:
+ Phương trình sin x = sin α, với α là một số cho trước, có các nghiệm là:
x = α + k2π k ∈ Z và x = π – α + k2π k ∈ Z
Tổng quát: sin f(x) = sin g(x)
+ sin x = sin β°
+ Các trường hợp đặc biệt:
a = 1: Phương trình sin x = 1 có các nghiệm là: x = π/2 + k2π k ∈ Z.
a = –1: Phương trình sin x = –1 có các nghiệm là: x = -π/2 + k2π k ∈ Z.
a = 0: Phương trình sin x = 0 có các nghiệm là: x = x = kπ k ∈ Z.
Xem thêm
Câu 27:
04/01/2025Cho sinx=13, x∈(0;π2). Tính giá trị của tanx
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Lời giải
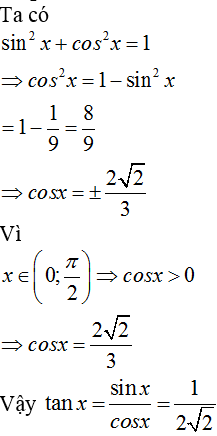
*Phương pháp giải:
Áp dụng công thức lượng giác cơ bản
*Lý thuyết:
1.
Xem thêm
Công thức lượng giác và cách giải bài tập chi tiết nhất
Bài thi liên quan
-
Bài tập Lượng giác từ đề thi Đại học cơ bản, nâng cao (P1)(Đề số 1)
-
30 câu hỏi
-
50 phút
-
-
Bài tập Lượng giác từ đề thi Đại học cơ bản, nâng cao (P1) (Đề số 3)
-
30 câu hỏi
-
50 phút
-
-
Bài tập Lượng giác từ đề thi Đại học cơ bản, nâng cao (P1) (Đề số 4)
-
20 câu hỏi
-
50 phút
-
Có thể bạn quan tâm
- 93 Bài tập trắc nghiệm Lượng giác lớp 11 có lời giải (P1) (1690 lượt thi)
- Bài tập Lượng giác ôn thi đại học có lời giải (P1) (386 lượt thi)
- 160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án (P1) (1343 lượt thi)
- Bài tập Giới hạn ôn thi đại học có lời giải (P1) (791 lượt thi)
- 15 câu lượng giác cơ bản , nâng cao (có đáp án) (p1) (359 lượt thi)
- Bài tập Lượng giác từ đề thi Đại học cơ bản, nâng cao (P1) (1066 lượt thi)
- 299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (3500 lượt thi)
- Bài tập Tổ Hợp - Xác Suất từ đề thi đại học cực hay có lời giải (P1) (1577 lượt thi)
- Bài tập Phép dời hình và phép đồng dạng trong mặt phẳng từ đề thi Đại Học (P1) (376 lượt thi)
- Bài tập Lượng giác từ đề thi đại học cơ bản, nâng cao có đáp án (P1) (1098 lượt thi)