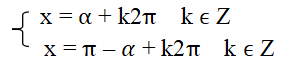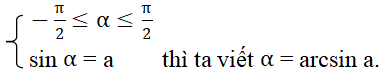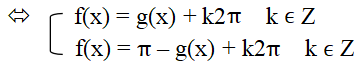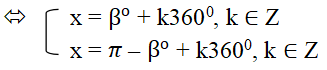Câu hỏi:
17/06/2026 7,330Cho phương trình . Tính tổng các nghiệm thuộc khoảng của phương trình trên.
A.
B.
C.
D.
Trả lời:
Giải bởi Vietjack
Đáp án đúng là B
Lời giải
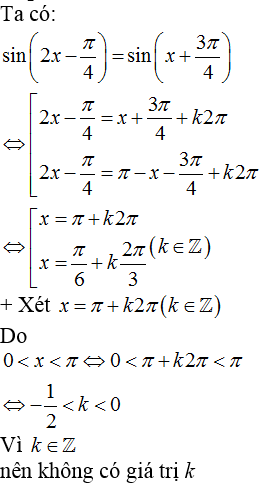
*Phương pháp giải:
Sử dụng phương trình sin
Xét hai trường hợp để tìm k
Kết luận
*Lý thuyết:
. Phương trình sin x = a (1)
- Trường hợp |a| > 1: Phương trình (1) vô nghiệm
- Trường hợp |a| ≤ 1: Phương trình (1) có các nghiệm là
+ Nếu số thực α thoả mãn điều kiện
- Lưu ý:
+ Phương trình sin x = sin α, với α là một số cho trước, có các nghiệm là:
x = α + k2π k ∈ Z và x = π – α + k2π k ∈ Z
Tổng quát: sin f(x) = sin g(x)
+ sin x = sin β°
+ Các trường hợp đặc biệt:
a = 1: Phương trình sin x = 1 có các nghiệm là: x = π/2 + k2π k ∈ Z.
a = –1: Phương trình sin x = –1 có các nghiệm là: x = -π/2 + k2π k ∈ Z.
a = 0: Phương trình sin x = 0 có các nghiệm là: x = x = kπ k ∈ Z.
Xem thêm
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tính tổng tất cả các nghiệm của phương trình sinx+sin2x=0 trên đoạn [0;2p ]
Câu 3:
Trên đường tròn lượng giác số điểm biểu diễn tập nghiệm của phương trình là
Câu 5:
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên đoạn
Câu 7:
Phương trình nào dưới đây có tập nghiệm biểu diễn trên đường tròn lượng giác là hai điểm M, N
Câu 9:
Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình bằng
Câu 14:
Có bao nhiêu giá trị nguyên m để phương trình dưới đây có nghiệm?
