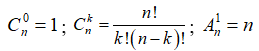40 câu hỏi trắc nghiệm thuộc 299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 2)

Cho số nguyên dương n và số nguyên dương k với 0 ≤ k ≤ n. Mệnh đề nào sau đây đúng?

$A . C_{n}^{k} = C_{n}^{n - k}$

$B . C_{n}^{k} = C_{n - k}^{n}$

$C . C_{n}^{k} = C_{n}^{k + 1}$

$D . C_{n}^{k} = C_{n + 1}^{n - k}$

Xem đáp án

Chọn A

Câu 2:

Công thức tính tổ hợp chập k của n và cách giải các dạng bài tập

Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau lập từ các chữ số 1, 2, 3, 4, 5, 6

A. 20 số

B. 216 số

C. 729 số

D. 120 số

Xem đáp án

Chọn D

Mỗi số lập được là một chỉnh hợp chập 3 của 6 phần tử.

Vậy lập được tất cả là $A_{6}^{3}$ = 120 số

Câu 3:

20/07/2024

Cho tập hợp A = {1,2,3,...,10}. Một tổ hợp chập 2 của các phần tử tập A là

A. {1;2}

B. $C_{10}^{2}$

C. $A_{10}^{2}$

D. (1;2)

Xem đáp án

Chọn A

Một tổ hợp chập 2 của các phần tử tập A là một tập con bất kỳ chứa 2 phần tử của A.

Câu 4:

10/11/2024

Một tổ có 10 học sinh. Hỏi có bao nhiêu cách chọn ra 2 học sinh từ tổ đó để giữ 2 chức vụ tổ trưởng và tổ phó.

$A . C_{10}^{2}$

$B . A_{10}^{8}$

$C . 10^{2}$

$D . A_{10}^{2}$

Xem đáp án

Đáp án đúng là D

Lời giải

Theo yêu cầu bài toán thì chọn ra 2 học sinh từ 10 học sinh có quan tâm đến chức vụ của mỗi người nên mỗi cách chọn sẽ là một chỉnh hợp chập 2 của 10 phần tử.

*Phương pháp giải:

Áp dụng công thức chình hợp

*Lý thuyết:

Một chỉnh hợp chập k của n là một cách sắp xếp có thứ tự k phần tử từ một tập hợp n phần tử (với k, n là các số tự nhiên, 1 ≤ k ≤ n).

Số các chỉnh hợp chập k của n, kí hiệu là $A_{n}^{k}$ , được tính bằng công thức:

$A_{n}^{k}$ = n.(n – 1)…(n – k + 1) hay $A_{n}^{k} = \frac{n!}{(n - k)!}$ (1 ≤ k ≤ n).

Chú ý :

+ Hoán vị sắp xếp tất cả các phần tử của tập hợp, còn chỉnh hợp chọn ra một số phần tử và sắp xếp chúng.

+ Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử đó. Vì vậy P_n = $A_{n}^{n}$

Xem thêm

TOP 40 câu Trắc nghiệm Hoán Vị - Chỉnh Hợp – Tổ Hợp (có đáp án ) – Toán 11

Câu 5:

Với k, n là số nguyên dương 1≤k ≤ n. Đẳng thức nào sau đây là đúng?

$A . C_{n}^{k - 1} + C_{n + 1}^{k} = C_{n + 1}^{k + 1}$

$B . C_{n - 1}^{k - 1} + C_{n}^{k} = C_{n + 1}^{k}$

$C . C_{n}^{k - 1} + C_{n}^{k} = C_{n + 1}^{k + 1}$

$D . C_{n}^{k - 1} + C_{n}^{k} = C_{n + 1}^{k}$

Xem đáp án

Chọn D

Theo tính chất của tổ hợp.

Câu 6:

Chọn kết luận đúng

$A . A_{n}^{k} = \frac{n!}{(n - k)!}$

$B . A_{n}^{k} = 0$

$C . C_{n}^{k} = \frac{n!}{k! (n + k)!}$

$D . A_{n}^{1} = 1$

Xem đáp án

Chọn A

Theo công thức số chỉnh hợp.

Mặt khác

Câu 7:

Trong các công thức sau, công thức nào đúng?

$A . C_{n}^{k} = \frac{A_{n}^{k}}{k}$

$B . A_{n}^{k} = \frac{n!}{(n - k)!}$

$C . C_{n}^{k} = \frac{n!}{k (n - k)!}$

$D . A_{n}^{k} = \frac{n!}{(n - k)}$

Xem đáp án

Chọn B

Câu 8:

Lý thuyết Tổ hợp chi tiết – Toán lớp 10 Cánh diều

Với k và n là hai số nguyên dương tùy ý thỏa mãn k $\leq$ n , mệnh đề nào dưới đây đúng?

$A . C_{n}^{k} = \frac{n!}{(n - k)!}$

$B . C_{n}^{k} = \frac{k! (n - k)!}{n!}$

$C . C_{n}^{k} = \frac{n!}{k!}$

$D . C_{n}^{k} = \frac{n!}{k! (n - k)!}$

Xem đáp án

Chọn D

Câu 9:

24/11/2024

Cho tập hợp S gồm 5 phần tử. Số tập con gồm 2 phần tử của S là:

$A . 30$

$B . 5^{2}$

$C . C_{5}^{2}$

$D . A_{5}^{2}$

Xem đáp án

Đáp án đúng là C

Lời giải:

Số tập hợp con có 2 phần tử của A là $C_{5}^{2}$ .

*Phương pháp giải:

Sử dụng định nghĩa:

Cho tập hợp A gồm n phần tử và một số nguyên k với 1 ≤ k ≤ n.

Mỗi tập con gồm k phần tử được lấy ra từ n phần tử của A được gọi là một tổ hợp chập k của n phần tử đó.

*Lý thuyết:

1. Định nghĩa

Cho tập hợp A gồm n phần tử và một số nguyên k với 1 ≤ k ≤ n.

Mỗi tập con gồm k phần tử được lấy ra từ n phần tử của A được gọi là một tổ hợp chập k của n phần tử đó.

Ví dụ: Bạn Mai có 4 chiếc váy màu hồng, màu đỏ, màu trắng, màu tím. Mai muốn chọn 3 trong 4 chiếc váy để mang đi du lịch. Hãy viết các tổ hợp 3 của 4 chiếc áo váy đó.

Hướng dẫn giải

Các tổ hợp chập 3 của 4 chiếc váy là :

Hồng – đỏ – trắng ; Hồng – đỏ – tím ; Đỏ – trắng – tím ; Hồng – trắng – tím.

Vậy ta có 4 tổ hợp chập 3 của 4 chiếc váy là : Hồng – đỏ – trắng ; Hồng – đỏ – tím ; Đỏ – trắng – tím ; Hồng – trắng – tím.

2. Số các tổ hợp

Nhận xét : Một tổ hợp chập k của n phần tử nhiều gấp k! lần số tổ hợp chập k của n phần tử đó.

Kí hiệu là $C_{n}^{k}$ là số tổ hợp chập k của n phần tử với (1 ≤ k ≤ n). Ta có : $C_{n}^{k} = \frac{A_{n}^{k}}{k!}$

Quy ước 0! = 1 ; $C_{n}^{0} = 1$ .

Với những quy ước trên, ta có công thức sau: $C_{n}^{k} = \frac{n!}{(n - k)! k!}$ (với 0 ≤ k ≤ n).

Ví dụ: Một tổ có 8 người, bạn tổ trưởng muốn cử ra 4 bạn đi tập văn nghệ. Hỏi có bao nhiêu cách chọn ?

Hướng dẫn giải

Mỗi cách chọn 4 bạn trong 8 bạn đi trực nhật là một tổ hợp chập 4 của 8.

Ta có $C_{8}^{4} = \frac{8!}{(8 - 4)! 4!} = 70$ .

Vậy có 70 cách chọn 4 trong 8 bạn đi tập văn nghệ.

3. Tính chất của các số $C_{n}^{k}$

Ta có hai đẳng thức sau : $C_{n}^{k} = C_{n}^{n - k}$ (0 ≤ k ≤ n) và $C_{n - 1}^{k - 1} + C_{n - 1}^{k} = C_{n}^{k}$ (1 ≤ k < n).

Ví dụ: Ta có : $C_{10}^{6} = C_{10}^{10 - 6} = 210$ ; $C_{10 - 1}^{6 - 1} + C_{10 - 1}^{6} = C_{10}^{6} = 210$ .

Xem thêm

TOP 40 câu Trắc nghiệm Hoán Vị - Chỉnh Hợp – Tổ Hợp (có đáp án ) – Toán 11

Câu 10:

50 Bài tập Hoán vị - Chỉnh hợp - Tổ hợp Toán 11 mới nhất

Cho n $\in$ N và n! = 1. Số giá trị của n thỏa mãn giả thiết đã cho là

A. 1.

B. 2.

C. 0.

D. Vô số.

Xem đáp án

Chọn B

Ta có 0! = 1 và 1! = 1. Vậy có 2 giá trị của thỏa mãn.

Câu 11:

05/11/2024

Với k và n là hai số nguyên dương tùy ý thỏa mãn k ≤ n. Mệnh đề nào sau đây đúng?

$A . C_{n}^{k} = \frac{n!}{k!}$

$B . A_{n}^{k} = \frac{n!}{(n - k)!}$

$C . C_{n}^{k} = \frac{k! (n - k)!}{n!}$

$D . A_{n}^{k} = \frac{n!}{k! (n - k)!}$

Xem đáp án

Đáp án đúng là :B.

*Phương pháp giải:

Dựa vào công thức chỉnh hợp

*Lý thuyết

Dựa vào công thức tính số các chỉnh hợp chập k của một tập hợp có nphần tử và công thức tính số các tổ hợp chập của một tập hợp có n phần tử nên ta có mệnh đề đúng là $A_{n}^{k} = \frac{n!}{(n - k)!}$

Xem them

Chuyên đề Hoán vị - Chỉnh hợp - Tổ hợp - Toán 11

Câu 12:

Số các tổ hợp chập k của một tập hợp có n phần tử 1 $\leq$ k $\leq$ n là :

$A . C_{n}^{k} = \frac{n!}{(n - k)!}$

$B . C_{n}^{k} = \frac{A_{n}^{k}}{k!}$

$C . C_{n}^{k} = \frac{A_{n}^{k}}{(n - k)!}$

$D . C_{n}^{k} = \frac{k! (n - k)!}{n!}$

Xem đáp án

Chọn B

Do 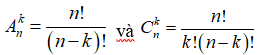nên $C_{n}^{k} = \frac{A_{n}^{k}}{k!}$ .

Câu 13:

Cho tập hợp M có 10 phần tử. Số tập hợp con gồm 2 phần tử của M là

$A . A_{10}^{8}$

$B . A_{10}^{2}$

$C . C_{10}^{2}$

$D . 10^{2}$

Xem đáp án

Chọn C

Số tập hợp con gồm k phần tử của tập n phần tử là: $C_{n}^{k}$ => Số tập hợp con gồm 2 phần tử của tập hợp M là $C_{10}^{2}$ .

Câu 14:

Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 41 học sinh?

$A . A_{41}^{2}$

$B . 41^{2}$

$C . 2^{41}$

$D . C_{41}^{2}$

Xem đáp án

Chọn D

Số cách chọn hai học sinh từ một nhóm gồm 41 học sinh là số tổ hợp chập 2 của 41, tức có $C_{41}^{2}$ cách chọn.

Câu 15:

Với k và n là hai số nguyên dương tùy ý thỏa mãn k≤n , mệnh đề nào dưới đây đúng?

$A . P_{n} = \frac{n!}{(n - k)!}$

$B . P_{n} = (n - k)!$

$C . P_{n} = \frac{n!}{k!}$

$D . P_{n} = n!$

Xem đáp án

Chọn D

Câu 16:

Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là

$A . C_{n}^{k} = \frac{n!}{(n - k)!}$

$B . C_{n}^{k} = \frac{n!}{k! (n - k)!}$

$C . A_{n}^{k} = \frac{n!}{(n - k)!}$

$D . A_{n}^{k} = \frac{n!}{k! (n - k)!}$

Xem đáp án

Chọn C

Câu 17:

Cho k, n, 1 $\leq$ k $\leq$ n là các số nguyên dương bất kì. Mệnh đề nào sau đây sai?

$A . C_{n}^{k} = \frac{A_{n}^{k}}{k!}$

$B . C_{n}^{k} = \frac{A_{n}^{k}}{(n - k)!}$

$C . C_{n}^{k} = \frac{n!}{k! (n - k)!}$

$D . A_{n}^{k} = \frac{n!}{(n - k)!}$

Xem đáp án

Chọn B

Số các chỉnh hợp chập k của một tập có n phần tử, kí hiệu là: $A_{n}^{k} = \frac{n!}{(n - k)!}$ , (1 $\leq$ k $\leq$ n)

=> D đúng

Số các tổ hợp chập k của một tập có n phần tử, kí hiệu là: $C_{n}^{k} = \frac{n!}{k! (n - k)!}$ , (1 $\leq$ k $\leq$ n)

=> C đúng

Ta có :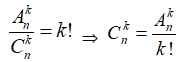

=> A đúng

Câu 18:

Cho n $\geq$ 2, n $\in$ N thỏa mãn : $A_{n}^{3} + C_{n}^{2} = 14 n$ . Giá trị của n là

A. 3.

B. 4.

C. 5.

D. 6.

Xem đáp án

Chọn C

Sử dụng công thức: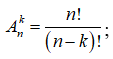

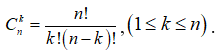
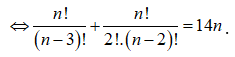
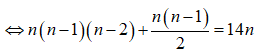
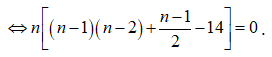
Ta có: $A_{n}^{3} + C_{n}^{2} = 14 n$

Câu 19:

Có bao nhiêu cách chia 20 chiếc bút chì giống nhau cho ba bạn Bắc, Trung, Nam sao cho mỗi bạn được ít nhất một chiếc bút chì

A. 153

B. 210

C. 190

D. 171

Xem đáp án

Chọn D

Xếp 20 chiếc bút chì thành một hàng ngang, giữa chúng có 19 chỗ trống.

Số cách chia bút chì thỏa mãn điều kiện đề bài chính là số cách đặt 2 “vách ngăn” vào 2 chỗ trống trong số 19 chỗ trống nói trên (mỗi chỗ trống được chọn đặt 1 “vách ngăn”), tức là bằng $C_{19}^{2}$ = 171.

Câu 20:

Mệnh đề nào sau đây sai ?

A. Số tập con có 4 phần tử của tập 6 phần tử là $C_{6}^{4}$ .

B. Số cách xếp 4 quyển sách vào 4 trong 6 vị trí trên giá là $A_{6}^{4}$ .

C. Số cách chọn và xếp thứ tự 4 học sinh từ nhóm 6 học sinh là $C_{6}^{4}$ .

D. Số cách xếp 4 quyển sách trong 6 quyển sách vào 4 vị trí trên giá là $A_{6}^{4}$ .

Xem đáp án

Chọn C

A đúng. Cứ 4 phần tử bất kì từ tập 6 phần tử ta sẽ được một tập con của tập 6 phần tử. Số tập con có 4 phần tử là $C_{6}^{4}$ .

B đúng. Khi đảo vị trí của 4 quyển sách sẽ được 1 cách sắp xếp mới (có sắp thứ tự). Do vậy số cách xếp 4 quyển sách vào 4 trong 6 vị trí trên giá là $A_{6}^{4}$ .

C sai. Mỗi cách lựa chọn và xếp thứ tự 4 học sinh từ nhóm 6 học sinh là một chỉnh chập 4 của 6 học sinh. Vậy số cách lựa chọn và xếp thứ tự 4 học sinh từ nhóm 6 học sinh là $A_{6}^{4}$ .

D đúng. Mỗi cách sắp xếp 4 quyển sách trong 6 quyển sách vào 4 vị trí là một chỉnh hợp chập 4 của 6 quyển sách. Vậy số cách sắp xếp 4 quyển sách trong 6 vào 4 vị trí trên giá là $A_{6}^{4}$ .

Phân tích: Đây là kiến liên quan đến bài toán đếm. Yêu cầu học sinh phải hiểu được tổ hợp và chỉnh hợp. Sự lựa chọn có sắp thứ tự và không sắp thứ tự.

- Cho tập A gồm n phần tử và số nguyên k với 1 $\leq$ k $\leq$ n Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự ta được một chỉnh hợp chập k của n phần tử của A. Kí hiệu $A_{n}^{k}$ .

- Cho tập A có n phần tử và số nguyên k với 1 $\leq$ k $\leq$ n . Mỗi tập con của A có k phần tử được gọi là một tổ hợp chập k của n phần tử của A. Kí hiệu $C_{n}^{k}$ .

Câu 21:

Mệnh đề nào sau đây sai ?

A. Số cách chọn một tổ văn nghệ gồm 3 em tùy ý từ lớp 10A1 gồm 35 em là $C_{35}^{3}$ .

B. Số cách xếp 3 quyển sách vào 3 trong 6 vị trí trên giá là $A_{6}^{3}$ .

C. Số cách cắm 3 bông hoa vào 5 bình hoa (mỗi bông cắm 1 bình) là $C_{5}^{3}$ .

D. Số cách xếp 4 quyển sách trong quyển sách vào 6 vị trí trên giá là $A_{6}^{4}$ .

Xem đáp án

Chọn C

Câu 22:

Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây không phải là phương trình mặt cầu?

A. $x^{2} + y^{2} + z^{2}$ - 1 = 0

B. $x^{2} + y^{2} + z^{2}$ + 2x - 4y + 2z + 17 = 0

C. $x^{2} + y^{2} + z^{2}$ + 2x - 4y + 6z + 5 = 0

D. $x^{2} + y^{2} + z^{2}$ - 2x + y - z = 0

Xem đáp án

Chọn B

Cho (S):

Điều kiện để (S) là phương trình của một mặt cầu là:

Ở câu A, nên đây là phương trình của mặt cầu.

Ở câu B, = -11 < 0 nên đây không phải là phương trình của mặt cầu.

Ở câu C, = 9 > 0 nên đây là phương trình của mặt cầu.

Ở câu D, 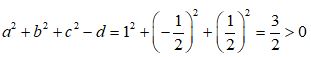nên đây là phương trình của mặt cầu.

Câu 23:

Một đội văn nghệ có 10 người gồm 6 nam và 4 nữ. Cần chọn ra một bạn nam và một bạn nữ để hát song ca. Hỏi có bao nhiêu cách chọn?

A. 1

B. 24

C. 10

D. $C_{10}^{2}$

Xem đáp án

Chọn B

Số cách chọn một bạn nam và một bạn nữ để hát song ca là $C_{6}^{1} . C_{4}^{1} = 24$

Câu 24:

Có bao nhiêu cách sắp xếp 5 học sinh theo một hàng ngang?

A. 10.

B. 24.

C. 5.

D. 120.

Xem đáp án

Chọn D

Mỗi cách sắp xếp 5 học sinh là một hoán vị của 5 phần tử. Vậy có 5! = 120 cách.

Câu 25:

18/07/2024

Số các chỉnh hợp chập k của một tập hợp gồm n phần tử (với k,n $\in ℕ^{*}, k \leq n$ ).

$A . \frac{k!}{(k - n)!}$

$B . C_{n}^{k} . k! .$

$C . C_{n}^{k} . (n - k)! .$

$D . \frac{k! (n - k)!}{n!}$

Xem đáp án

Chọn B

Ta có số chỉnh hợp chập k của một tập hợp gồm n phần tử là: .

Câu 26:

Mệnh đề nào sau đây sai?

A. Số tập con có 2 phần tử của tập 6 phần tử là $C_{6}^{2}$ .

B. Số tam giác được tạo ra từ 9 điểm phân biệt (trong đó không có 3 điểm nào thẳng hàng) là $C_{9}^{3}$ .

C. Số vecto tối đa tạo bởi 20 điểm phân biệt là $C_{20}^{2}$ .

D. Số cách xếp 3 quyển sách trong quyển sách vào 7 vị trí trên giá là $A_{7}^{3}$ .

Xem đáp án

Chọn C

Câu 27:

18/07/2024

Trong tủ quần áo của bạn An có 4 chiếc áo khác nhau và 3 chiếc quần khác nhau. Hỏi bạn An có bao nhiêu cách để chọn 1 bộ quần áo để mặc?

A. 7

B. 27

C. 64

D. 12

Xem đáp án

Chọn D

Chọn một bộ quần áo, cần thực hiện liên tiếp hai hành động:

Hành động 1 - chọn áo: có 4 cách chọn.

Hành động 2 - chọn quần: ứng với mỗi cách chọn áo có 3 cách chọn quần.

Vậy số cách chọn một bộ quần áo là: 4.3 = 12 (cách).

Câu 28:

Cho tập M = {1;2;3;4;5;6;7;8;9}. Có bao nhiêu tập con có 4 phần tử lấy từ các phần tử của tập M?

$A . 4^{9}$

$B . C_{9}^{4}$

$C . 4!$

$D . A_{9}^{4}$

Xem đáp án

Chọn B

Theo Định nghĩa Tổ hợp. Ta có số tập con có 4 phần tử lấy từ các phần tử của tập 4 là $C_{9}^{4}$ .

Câu 29:

Cho tập hợp A gồm có 9 phần tử. Số tập con gồm có 4 phần tử của tập hợp A là

A. $C_{9}^{4}$

B. $P_{4}$

C. 36

D. $A_{9}^{4}$

Xem đáp án

Chọn A

Ta lấy 4 phần tử bất kì trong tập hợp gồm 9 phần tử có $C_{9}^{4}$ cách.

Vậy số tập con gồm 4 phần tử là $C_{9}^{4}$

Câu 30:

Với k và n là hai số nguyên dương tùy ý thỏa mãn k $\leq$ n, mệnh đề nào dưới đây đúng?

$A . A_{n}^{k} = \frac{n!}{(n - k)!}$

$B . A_{n}^{k} = \frac{n!}{k! (n - k)!}$

$C . A_{n}^{k} = \frac{n!}{k!}$

$D . A_{n}^{k} = \frac{k! (n - k)!}{n!}$

Xem đáp án

Chọn A

Câu 31:

Cho n là số tự nhiên lớn hơn 2. Số các chỉnh hợp chập 2 của n phần tử là

A. $\frac{n (n - 1)}{2!}$

B. 2!.n.(n-1)

C. n.(n-1)

D. 2n

Xem đáp án

Chọn C

Ta có:

Câu 32:

Một tổ có 10 học sinh. Số cách chọn ra 2 học sinh từ tổ đó để giữ 2 chức vụ tổ trưởng và tổ phó là

$A . C_{10}^{2}$

$B . A_{10}^{2}$

$C . 10^{2}$

$D . A_{10}^{8}$

Xem đáp án

Chọn B

Chọn 2 trong 10 học sinh để giữ 2 chức vụ tổ trưởng và tổ phó (có thứ tự ) là chỉnh hợp chập 2 của 10 => $A_{10}^{2}$ (cách).

Câu 33:

Với k và n là hai số nguyên dương tùy ý thỏa mãn k ≤ n, mệnh đề nào dưới đây đúng?

$A . A_{n}^{k} = \frac{n!}{k!}$

$B . A_{n}^{k} = \frac{n!}{k! (n - k)!}$

$C . A_{n}^{k} = \frac{k! (n - k)!}{n!}$

$D . A_{n}^{k} = \frac{n!}{(n - k)!}$

Xem đáp án

Chọn D

Công thức chỉnh hợp.

Câu 34:

Số cách xếp 3 người ngồi vào 5 ghế xếp thành hàng ngang sao cho mỗi người ngồi một ghế là

A. $A_{5}^{3}$

B. $C_{5}^{3}$

C. 5!

D. 3!

Xem đáp án

Chọn A

Mỗi cách xếp 3 người ngồi vào 5 ghế xếp thành hàng ngang sao cho mỗi người ngồi một ghế là một chỉnh hợp chập 3 của 5 phần tử. Do đó số cách xếp là $A_{5}^{3}$

Câu 35:

18/07/2024

Số các số tự nhiên gồm ba chữ số khác nhau lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8 là

$A . C_{8}^{3}$

$B . P_{8}$

$C . A_{8}^{3}$

$D . P_{3}$

Xem đáp án

Chọn C

Câu 36:

Cho n điểm phân biệt trên mặt phẳng (n $\in ℕ$ , n > 2). Số véctơ khác $\overset{⇀}{0}$ có cả điểm đầu và điểm cuối là các điểm đã cho bằng

A. n(n-1)

B. $\frac{n (n - 1)}{2}$

C. 2n(n-1)

D. 2n

Xem đáp án

Chọn A

Hai điểm bất kì trong n điểm trên tạo thành hai véctơ thỏa mãn yêu cầu bài toán. Nên số các véc tơ đó là:

Nhận xét: Có thể hiểu mỗi véctơ là một chỉnh hợp chập 2 của n điểm. Nên số véctơ là:

Câu 37:

Với k và n là hai số nguyên dương tùy ý thỏa mãn k $\leq$ n, mệnh đề nào dưới đây sai?

$A . C_{n}^{k} + + C_{n}^{k - 1} = C_{n + 1}^{k}$

$B . A_{n}^{k} = \frac{n!}{k! (n - k)!}$

$C . A_{n}^{k} = C_{n}^{k} . k!$

$D . C_{n}^{k} = C_{n}^{n - k}$

Xem đáp án

Chọn B

Với k và n là hai số nguyên dương thỏa k $\leq$ n ta có:

Số các chỉnh hợp chập k của n phần tử là: $A_{n}^{k} = \frac{n!}{(n - k)!}$ , nên câu B sai.

Câu 38:

Cho tập hợp A có 26 phần tử. Hỏi A có bao nhiêu tập con gồm 6 phần tử?

A. $C_{26}^{6}$

B. 26

C. $P_{6}$

D. $A_{26}^{6}$

Xem đáp án

Chọn A

Số tập con có 6 phần tử của tập A là $C_{26}^{6}$

Câu 39:

Một lớp học có 40 học sinh, biết rằng các bạn đều có khả năng được chọn như nhau, số cách chọn ra ba bạn để phân công làm tổ trưởng tổ 1, tổ 2 và tổ 3 là

$A . A_{40}^{3}$

$B . C_{40}^{3}$

$C . 3!$

$D . 3 C_{40}^{3}$

Xem đáp án

Chọn A

Mỗi cách chọn ra 3 học sinh từ 40 học sinh để làm tổ trưởng tổ 1, tổ 2, tổ 3 là một chỉnh hợp chập 3 của 40 phần tử, vậy có: $A_{40}^{3}$ (cách).

Câu 40: