299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1)
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 5)
-
3546 lượt thi
-
40 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Tìm hệ số của số hạng chứa x3 trong khai triển nhị thức Niutơn (2x-1)6
 Xem đáp án
Xem đáp án
Chọn D
Xét khai triển nhị thức Niutơn: (2x-1)6 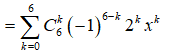
Số hạng chứa x3 trong khai triển ứng với k = 3.
Vậy hệ số của số hạng chứa x3 trong khai triển là: ![]() .
.
Câu 2:
22/07/2024Hệ số của số hạng chứa x4 trong khai triển (2+3x)5 là
 Xem đáp án
Xem đáp án
Chọn B.
(2+3x)5 có công thức số hạng tổng quát là: ![]() .
.
Với k = 4, ta được số hạng ![]() .
.
Vậy hệ số của số hạng chứa x4 trong khai triển (2+3x)5 là 810.
Câu 3:
18/07/2024(x+2)n+5, Khai triển nhị thức có tất cả 2019 số hạng. Tìm n.
 Xem đáp án
Xem đáp án
Chọn C
Khai triển có tất cả 2019 số hạng nên (n+5) + 1 = 2019 => n = 2013
Câu 4:
22/07/2024Cho biểu thức: P(x) = . Hệ số của số hạng chứa trong khai triển thành đa thức của P(x) là
 Xem đáp án
Xem đáp án
Chọn C
Ta có: 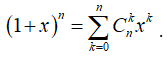 .
.
Số hạng tổng quát của khai triển là: ![]() . Hệ số của trong khai triển là:
. Hệ số của trong khai triển là:
Hệ số của số hạng chứa trong biểu thức P(x) là:
![]() .
.
Câu 5:
18/07/2024Số hạng không chứa z trong khai triển là?
 Xem đáp án
Xem đáp án
Chọn D
Có: 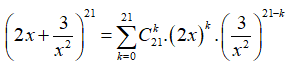
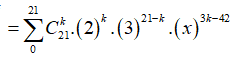
+ Số hạng không chứa x khi ![]()
![]()
+ Vậy số hạng không chứa x là ![]() .
.
Câu 6:
23/07/2024Tìm số hạng không chứa x trong khai triển nhị thức Newton
 Xem đáp án
Xem đáp án
Chọn A
Số hạng tổng quát của biểu thức khi khai triển theo công thức nhị thức Newton là 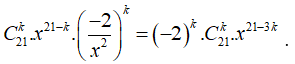
Số hạng không chứa x trong khai triển nhị thức Newton là ![]() với k thỏa mãn
với k thỏa mãn
21-3k = 0 => k = 7
Vậy số hạng không chứa x trong khai triển nhị thức Newton là ![]()
Câu 7:
21/07/2024Cho khai triển với n là số nguyên dương. Tìm hệ số của số hạng chứa trong khai triển biết .
 Xem đáp án
Xem đáp án
Chọn D
Ta có: ![]()
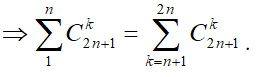
Ta có: 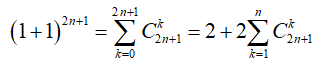
![]()
Hệ số của số hạng chứa là: = 120.
Câu 8:
23/07/2024Hệ số của trong khai triển biểu thức bằng.
 Xem đáp án
Xem đáp án
Chọn D
Hệ số của trong khai triển biểu thức là hệ số của trong khai triển biểu thức và bằng ![]() .
.
Hệ số của trong khai triển biểu thức là hệ số của trong khai triển biểu thức và bằng ![]() .
.
Vậy hệ số của trong khai triển biểu thức bằng 3240 + 80 = 3320.
Câu 9:
20/07/2024Tìm hệ số của số hạng không chứa x trong khai triển
 Xem đáp án
Xem đáp án
Chọn A
Số hạng tổng quát trong khai triển là 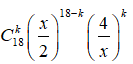
![]() .
.![]()
Số hạng không chứa x nên 18-2k = 0 => k = 9.
Hệ số của số hạng không chứa x trong khai triển là .
Câu 10:
22/07/2024Trong khai triển , số hạng không chứa x là
 Xem đáp án
Xem đáp án
Chọn B
Với x0, ta có
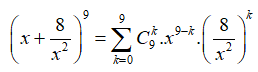
![]()
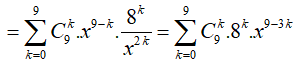
Từ yêu cầu bài toán suy ra 9 - 3k = 0 => k = 3, suy ra số hạng không chứa x là ![]() .
.
Câu 11:
22/07/2024Tìm hệ số của số hạng chứa trong khai triển
 Xem đáp án
Xem đáp án
Chọn D
Số hạng tổng quát trong khai triển biểu thức ![]() là
là ![]()
![]()
Số hạng chứa ứng với k = 5, suy ra hệ số của số hạng chứa là:
![]()
Câu 12:
18/07/2024Số hạng không chứa x trong khai triển là
 Xem đáp án
Xem đáp án
Chọn A
Số hạng tổng quát trong khai triển , x0 là  ,
, ![]() . Số hạng không chứa x ứng với 12-4k = 0 => k = 3.
. Số hạng không chứa x ứng với 12-4k = 0 => k = 3.
Vậy số hạng không chứa x trong khai triển trên là -1760.
Câu 13:
23/07/2024Tìm hệ số của số hạng chứa trong khai triển .
 Xem đáp án
Xem đáp án
Chọn B
Ta có:
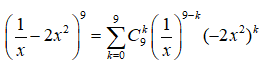
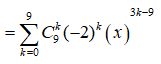
Hệ số cuả số hạng chứa tương ứng với 6 = 3k - 9 => k = 5
Vậy hệ số cuả số hạng chứa là
Câu 14:
16/07/2024Hệ số của trong khai triển biểu thức P(x) = x bằng
 Xem đáp án
Xem đáp án
Chọn D
Số hạng tổng quát của khai triển ![]()
![]()
![]()
Số hạng chứa trong A(x) là![]()
Số hạng tổng quát của khai triển ![]()
![]()
![]()
Số hạng chứa trong B(x) là ![]()
Vậy hệ số của số hạng chứa trong khai triển P(x) đã cho là 240-13608 = -13368.
Câu 15:
20/07/2024Cho n là số nguyên dương thỏa mãn . Hệ số của số hạng chứa trong khai triển biểu thức bằng
 Xem đáp án
Xem đáp án
Chọn D
Điều kiện xác định: ![]() .
.
Khi đó
![]()
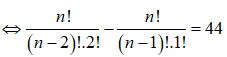
![]()

Kết hợp với điều kiện xác định suy ra n = 11
Ta có: 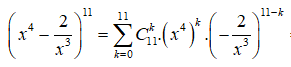
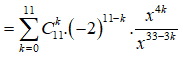
 .
.
Số hạng chứa ứng với k thỏa 7k - 33 = 9 => k = 6
Vậy hệ số của số hạng chứa là ![]() .
.
Câu 16:
20/07/2024Hệ số của trong khai triển của biểu thức là
 Xem đáp án
Xem đáp án
Chọn C
Số hạng tổng quát trong khai triển của biểu thức là ![]() .
.
Do đó hệ số của (ứng với k = 2) là ![]() .
.
Câu 17:
17/07/2024Trong khai triển nhị thức , số hạng không chứa x là:
 Xem đáp án
Xem đáp án
Chọn C.
Số hạng tổng quát trong khai triển là:
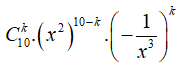
![]()
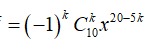
Số hạng không chứa x có số k thỏa mãn: 20 - 5k = 0 => k = 4
Vậy số hạng không chứa x đó là: ![]()
Câu 18:
23/07/2024Số hạng không chứa x trong khai triển bằng:
 Xem đáp án
Xem đáp án
Chọn D
Ta có: 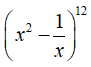

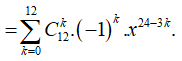
Vì số hạng không chứa x trong khai triển 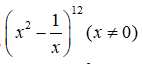 nên 24 - 3k = 0 => k = 8
nên 24 - 3k = 0 => k = 8
Vậy số hạng không chứa x trong khai triển là .
![]()
Câu 19:
27/10/2024Tìm số hạng không chứa x trong khai triển
 Xem đáp án
Xem đáp án
Đáp án đúng: B
* Lời giải:
Ta có 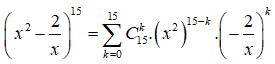
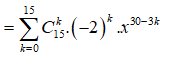
Số hạng không chứa x tương ứng với 30 - 3k = 0 => k = 10
Khi đó số hạng cần tìm là .
* Phương pháp giải:
- Khai triển áp dụng:
Công thức khai triển nhị thức Niu – tơn:
(a + b)n = 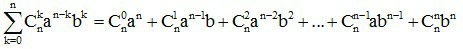
* Lý thuyết cần nắm thêm về tổ hợp - chỉnh hợp:
1) Chỉnh hợp
- Cho tập hợp A gồm n phần tử (n ≥ 1).
Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
Số các chỉnh hợp
- Kí hiệu là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n) .
- Định lí:
- Chú ý:
a) Với quy ước 0! = 1 ta có: .
b) Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử đó.
Vì vậy: .
2) Tổ hợp
Định nghĩa.
- Giả sử tập A có n phần tử (n ≥ 1). Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.
- Chú ý: Số k trong định nghĩa cần thỏa mãn điều kiện 1 ≤ k ≤ n. Tuy vậy, tập hợp không có phần tử nào là tập rỗng nên ta quy ước gọi tổ hợp chập 0 của n phần tử là tập rỗng.
Số các tổ hợp.
Kí hiệu là số các tổ hợp chập k của n phần tử ( 0 ≤ k ≤ n).
- Định lí: .
Tính chất của các số
Tính chất 1.
3) Nhị thức Newton:
Công thức khai triển nhị thức Niu – tơn:
(a + b)n = 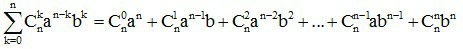
Các công thức
Phương pháp tìm tổng các hệ số trong khai triển
Xét khai triển tổng quát: (với a,b là các hệ số; x,y là biến)
(ax + by)n = 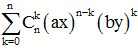
= Cn0anxn + Cn1an-1b.xn-1y + Cn2an-2b2.xn-2y2 + ...+Cnn-1abn-1.xyn-1 + Cnnbnyn
Tổng các hệ số trong khai triển là: S = Cn0an + Cn1an-1b + Cn2an-2b2 + ...+Cnn-1abn-1 + Cnnbn
Ta chọn biến x = 1; y = 1 thay vào khai triển: S = (a + b)n
(Chú ý: tùy thuộc vào khai triển đề bài cho, có thể xét khai triển với chỉ 1 biến x)
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Hoán vị - Chỉnh hợp - Tổ hợp (mới + Bài Tập) – Toán 11
Toán 11 Bài 2 giải SGK: Hoán vị - chỉnh hợp – tổ hợp
TOP 40 câu Trắc nghiệm Hoán Vị - Chỉnh Hợp – Tổ Hợp (có đáp án) – Toán 11
Câu 20:
18/07/2024Trong khai triển Newton của biểu thức , số hạng chứa là.
 Xem đáp án
Xem đáp án
Chọn B
Ta có: 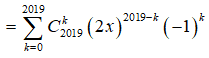
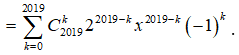
Số hạng tổng quát của khai triển là ![]() .
.
Để có thì 2019 - k = 18 => k = 2001.
Khi đó số hạng chứa là ![]() .
.
Câu 21:
18/07/2024Cho biểu thức P = với x > 0. Tìm số hạng không chứa x trong khai triển nhị thức Niutơn P.
 Xem đáp án
Xem đáp án
Chọn C
Số hạng tổng quát trong khai triển 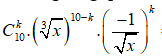
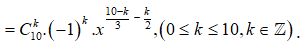 .
.
Số hạng không chứa x ứng với k thỏa mãn: 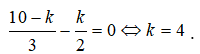 .
.
Vậy số hạng không chứa x cần tìm: ![]() .
.
Câu 22:
22/07/2024Biết tổng các hệ số trong khai triển nhị thức Newton của bằng . Tìm hệ số của .
 Xem đáp án
Xem đáp án
Chọn D
Ta có, 
 .
.
Tổng các hệ số trong khai triển bằng nên ta có phương trình:
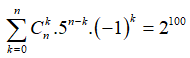
![]()
![]() .
.
Vậy 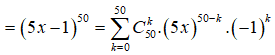
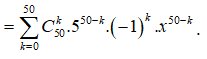 .
.
Xét số hạng chứa thì 50 - k = 3 => k = 47.
=> Hệ số của số hạng chứa là: ![]() .
.
Câu 23:
23/07/2024Tìm hệ số của số hạng chứa trong khai triển .
 Xem đáp án
Xem đáp án
Chọn B
Ta có có số hạng tổng quát là ![]() .
.
Số hạng chứa trong khai triển ứng với 8 - k = 5 => k = 3
Vậy hệ số của số hạng chứa trong khai triển là ![]() .
.
Câu 24:
23/07/2024Hệ số của trong khai triển của biểu thức bằng
 Xem đáp án
Xem đáp án
Chọn C
Số hạng tổng quát của khai triển:
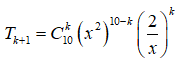
![]() .
.
Số hạng chứa ứng với: 20 - 3k = 2 => k = 6 (nhận).
Hệ số cần tìm là: ![]() .
.
Câu 25:
23/07/2024Tìm số hạng không chứa x trong khai triển , x0.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có 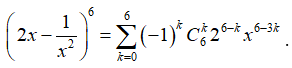 .
.
Số hạng thứ k + 1 là ![]() .
.
Tìm số hạng không chứa x trong khai triển khi: 6 - 3k = 0 => k = 2
Với k = 2 ta có số hạng không chứa x là: ![]() .
.
Câu 26:
22/07/2024Số hạng không chứa x trong khai triển bằng:
 Xem đáp án
Xem đáp án
Chọn C.
Phân tích: Bài toán này ta phải nhớ được kiến thức lớp 11 về Nhị thức Niu – Tơn 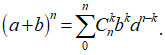 . Trong đó a, b thuộc số thực và n thuộc số tự nhiên và n 1. Số hạng tổng quát thứ k + 1 là:
. Trong đó a, b thuộc số thực và n thuộc số tự nhiên và n 1. Số hạng tổng quát thứ k + 1 là: ![]() .
.
Áp dụng vào bài toán ta có:
Số hạng tổng quát thứ k + 1 là: 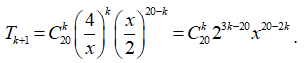 .
.
+) Vì số hạng không chứa x nên: 20 - 2k = 0 => k = 10
+) Vậy số hạng không chứa x là: ![]() .
.
Câu 27:
18/07/2024Cho đa thức f(x) = . Tìm hệ số , biết rằng: = 49152n
 Xem đáp án
Xem đáp án
Chọn D
Đạo hàm hai vế f(x)
![]()
![]()
![]()
Số hạng tổng quát thứ k + 1 trong khai triển thành đa thức của ![]()
![]()
Câu 28:
19/07/2024Hệ số trong khai triển đa thức P(x) = có giá trị bằng đại lượng nào sau đây?
 Xem đáp án
Xem đáp án
Chọn D
Số hạng tổng quát trong khai triển là ![]()
![]() .
.
Số hạng này chứa khi 10 - k = 6 => k = 4.
Do đó hệ số trong khai triển là: ![]() .
.
Câu 29:
12/07/2024Tính tổng các hệ số trong khai triển
 Xem đáp án
Xem đáp án
Chọn A
Đặt ![]()
Cho x = 1 ta có tổng các hệ số ![]()
Câu 30:
23/07/2024Số hạng không chứa x trong khai triển là
 Xem đáp án
Xem đáp án
Chọn D
Xét số hạng tổng quát
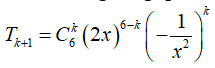

![]()
Số hạng không chứa x ứng với 6 - 3k = 0 => k = 2
Vậy số hạng không chứa x là ![]() .
.
Câu 31:
18/07/2024Tìm hệ số của số hạng chứa trong khai triển biết
 Xem đáp án
Xem đáp án
Chọn C
Ta có ![]()
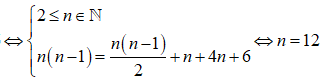 .
.
Xét khai triển 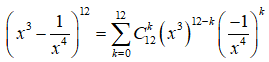
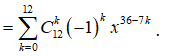 .
.
Số hạng chứa tương ứng với 36 - 7k = 8 => k = 4.
Vậy hệ số của số hạng chứa trong khai triển bằng ![]() .
.
Câu 32:
18/07/2024Cho số nguyên dương thỏa mãn = 0. Tìm hệ số của số hạng chứa trong khai triển nhị thức Niu-tơn của .
 Xem đáp án
Xem đáp án
Chọn B
Điều kiện xác định:  .
.
Ta có: 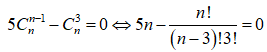
 .
.
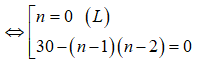 .
.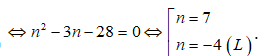
Khi đó nhị thức Niu-tơn 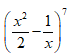 có số hạng tổng quát:
có số hạng tổng quát:

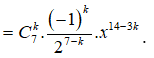 .
.
Số hạng chứa có giá trị k thỏa mãn: 14 - 3k = 5 => k = 3.
Vậy hệ số của số hạng chứa là: 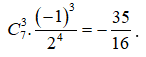 .
.
Câu 33:
14/07/2024Biết n là số nguyên dương thỏa mãn 3 số 0; theo thứ tự là số hạng đầu, số hạng thứ 3 và số hạng thứ 10 của một cấp số cộng. Hãy tìm số hạng không chứa x trong khai triển của
 Xem đáp án
Xem đáp án
Chọn A
Theo đề bài ta có: ![]()
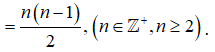 .
.
Lại theo tính chất của cấp số cộng có:
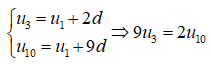
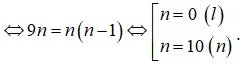
Khi đó số hạng tổng quát trong khai triển
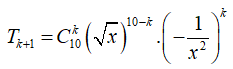
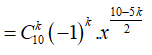
Số hạng không chứa x trong khai triển trên ứng với 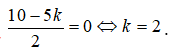
Vậy hệ số của số hạng không chứa x trong khai triển trên là ![]()
Câu 34:
18/07/2024Trong khai triển Newton của biểu thức , số hạng chứa là
 Xem đáp án
Xem đáp án
Chọn D
Số hạng tổng quát trong khai triển là
![]()
![]()
![]()
Theo đề bài ta có: 2019 - k = 18 => k = 2001.
Vậy trong khai triển biểu thức đã cho, số hạng chứa là:
![]()
![]()
Câu 35:
22/07/2024Cho số nguyên dương n thỏa mãn điều kiện: 720. Hệ số của trong khai triển bằng:
 Xem đáp án
Xem đáp án
Chọn B
Áp dụng công thức: ![]() ,
,![]() ta được:
ta được:
![]()
![]()
![]() .
.
Do đó : ![]()

![]()
Có: 
 .
.
Số hạng trong khai triển chứa ứng với 16 - 3k = 7 => k = 3
Vậy hệ số của là
Câu 36:
23/07/2024Cho khai triển . Hỏi có bao nhiêu giá trị của n 2019 sao cho tồn tại ![]() thỏa mãn .
thỏa mãn .
 Xem đáp án
Xem đáp án
Chọn D
Ta có: 
![]()
Số hạng tổng quát trong khai triển trên là ![]() nên từ giả thiết ta có
nên từ giả thiết ta có
![]()
Do đó: 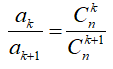
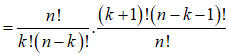
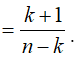
Suy ra: 
![]()
![]()
![]()
![]()
![]()
Thế vào (1), ta được: ![]()
![]()
Mặt khác, do ![]()
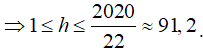
Với mỗi số nguyên dương h[1;91] tồn tại duy nhất một số nguyên dương n sao cho tồn tại k thỏa yêu cầu bài toán. Vậy có 91 số tự nhiên n.
Câu 37:
18/07/2024Cho n là số nguyên dương thỏa mãn = 78. Số hạng không chứa x trong khai triển bằng
 Xem đáp án
Xem đáp án
Chọn C
Điều kiện: ![]()
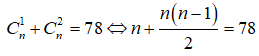
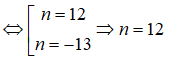 ( do điều kiện (1))
( do điều kiện (1))
Khi đó, 
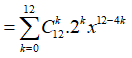
Số hạng không chứa x tương ứng 12 - 4k = 0 => k = 3
Suy ra số hạng không chứa x là: ![]()
Câu 38:
17/07/2024Cho khai triển , trong đó . Biết các hệ số thỏa mãn hệ thức . Hệ số bằng
 Xem đáp án
Xem đáp án
Chọn B
Ta có: ![]()
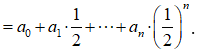
Trong khai triển thay x = ta được
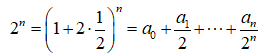
![]()
Số hạng tổng quát trong khai triển ![]()
Để có số hạng chứa thì k = 8.
Vậy ![]()
Câu 39:
18/07/2024Cho khai triển T =
 Xem đáp án
Xem đáp án
Chọn B
Cách 1:
![]()
![]()
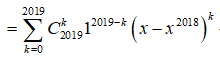
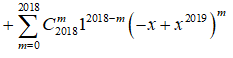

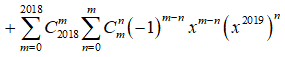
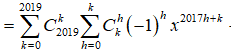

Với ![]()
![]()
Theo đề bài: 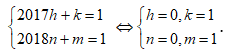
Hệ số của số hạng chứa x trong khai triển T là:
![]()
Cách 2:
Ta có: ![]() (với m = 4074342) (*)
(với m = 4074342) (*)
Lấy đạo hàm hai vế của (*) theo biến x:
![]()
![]()
Với x = 0, ta được: 2019 = .
Tương tự: ![]()
Lấy đạo hàm hai vế của (**) theo biến x:
![]()
![]()
Với x = 0, ta được: -2018 =
Hệ số của số hạng chứa x trong khai triển là: ![]()
Câu 40:
22/07/2024Tìm hệ số của số hạng chứa trong khai triển
 Xem đáp án
Xem đáp án
Chọn A
![]()
![]()
![]()
Ta có các cặp (k;m): 2k + m = 5
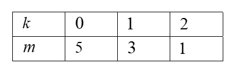
Suy ra hệ số của số hạng chứa là: ![]()
Bài thi liên quan
-
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 1)
-
40 câu hỏi
-
60 phút
-
-
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 2)
-
40 câu hỏi
-
60 phút
-
-
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 3)
-
40 câu hỏi
-
60 phút
-
-
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 4)
-
40 câu hỏi
-
60 phút
-
-
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 6)
-
40 câu hỏi
-
60 phút
-
-
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 7)
-
40 câu hỏi
-
60 phút
-
-
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 8)
-
40 câu hỏi
-
60 phút
-
-
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 9)
-
40 câu hỏi
-
60 phút
-
-
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (Đề số 10)
-
10 câu hỏi
-
60 phút
-
Có thể bạn quan tâm
- 93 Bài tập trắc nghiệm Lượng giác lớp 11 có lời giải (P1) (1707 lượt thi)
- Bài tập Lượng giác ôn thi đại học có lời giải (P1) (393 lượt thi)
- 160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án (P1) (1351 lượt thi)
- Bài tập Giới hạn ôn thi đại học có lời giải (P1) (795 lượt thi)
- 15 câu lượng giác cơ bản , nâng cao (có đáp án) (p1) (361 lượt thi)
- Bài tập Lượng giác từ đề thi Đại học cơ bản, nâng cao (P1) (1079 lượt thi)
- 299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (3545 lượt thi)
- Bài tập Tổ Hợp - Xác Suất từ đề thi đại học cực hay có lời giải (P1) (1593 lượt thi)
- Bài tập Phép dời hình và phép đồng dạng trong mặt phẳng từ đề thi Đại Học (P1) (379 lượt thi)
- Bài tập Lượng giác từ đề thi đại học cơ bản, nâng cao có đáp án (P1) (1106 lượt thi)
