Xếp 30 quyển truyện khác nhau có số cách là 30!

Ta tính số cách xếp 4 quyển 1, 3, 5, 7 cạnh nhau:

+) Hoán vị 1, 3, 5, 7 ta được 4! Cách.

+) Khi đã xếp 1, 3, 5, 7 cạnh nhau thì còn 26 vị trí, ứng với 26 vị trí này thì có 26! cách xếp.

Do đó xếp 4 quyển 1, 3, 5, 7 cạnh nhau có số cách là 4!.26!

Tóm lại có 30! – 4!26! cách xếp thỏa mãn.

Chọn B.

Xếp 6 viên bi xanh có 6! cách xếp, khi đó 6 viên bi xanh sẽ tạo thành 7 chỗ trống.

Xếp 4 viên bi vàng vào 7 chỗ trống đó là $A_7^4$  cách.

Do đó có  $A_7^4.6!=604800$ cách xếp.

Chọn A.

Chọn C.

Ta có  

• TH1. Nếu d = 0 thì a + b + c chia hết cho 3  

Mỗi bộ sau đều lập được 6 số: (1;2;3),(1;2;6),(1;3;5),(1;5;6),(2;3;7),(2;6;7),(3;5;7),(5;6;7)

• TH2. Nếu d = 5 thì a + b + c + 5 chia hết cho 3 

Mỗi bộ sau đều lập được 4 số: (0;1;3);(0;1;6);(0; 3; 7);  (0;6;7).

Mỗi bộ sau đều lập được 6 số: (1;2;7);(1;3;6); (3;6;7)

Tóm lại có tất cả 6.8+4.4+6.3=82 số thỏa mãn.

Chọn B.

Lời giải.

Cách 1:

Trong khai triển trên ta thấy bậc của x trong 3 số hạng đầu nhỏ hơn 8, bậc của x trong 4 số hạng cuối lớn hơn 8.

Do đó x⁸ chỉ có trong số hạng thứ tư, thứ năm với hệ số tương ứng là:.

Vậy hệ số cuả x⁸ trong khai triển đa thức  là: 

Cách 2: Ta có: 

với 0 ≤ k ≤ n ≤ 8. 

Số hạng chứa x⁸ ứng với 2n + k = 8 ⇒ k = 8 -2n là một số chẵn.

Thử trực tiếp ta được k = 0, n =4 và k = 2, n = 3.

Vậy hệ số của x⁸ là 

 Chọn C.

Ta có : 

Dễ dàng kiểm tra n=1; n=2 không thoả mãn điều kiện bài toán.

Với n ≥ 3 thì dựa vào khai triển ta chỉ có thể phân tích

Do đó hệ số của x^3n-3 trong khai triển thành đa thức của

Suy ra

Vậy n= 7là giá trị cần tìm.

Chọn C. 

Xét số hạng tổng quát.

Cho k chạy từ 1 đến 2018 ta được:

Cho x=1 suy ra 

Chọn A.

Giả sử 3 số  theo thứ tự đó lập thành một cấp số cộng khi và chỉ khi .

Với n=8 thì 

Với n=13 thì  

Chọn A.

Ta có  

Chọn B.

Ta có: 

Chọn x=1. Ta có tổng hệ số trong  khai triển bằng:

Lại có: 

Số hạng không chứa x suy ra 

Do đó số hạng không chứa x là: 

Chọn D.

Ta có n(Ω)= 6.6.6.6.6.6 = 6⁶  

Có các trường hợp sau:

1.Số bằng 5 xuất hiện đúng 5 lần ; 1 lần ra mặt khác 5 :  có 5 cách chọn số  khác 5.  

  Số kết quả thuận lợi là

2. Số bằng 5 xuất hiện đúng 6 lần có 1 kết quả thuận lợi.

3. Số bằng 6 xuất hiện đúng 5 lần; 1 lần  ra mặt khác 6: có 5 cách chọn  số khác 6.

Số kết quả thuận lợi là   

 4. Số bằng 6 xuất hiện đúng 6 lần có 1kết quả thuận lợi.

Vậy xác suất để được một số lớn hơn hay bằng 5 xuất hiện ít nhất 5 lần là 

 Chọn A.

Số phần tử của không gian mẫu là: 

Ta tính số phần tử của không gian thuận lợi

·       Cả hai bạn đều lấy ra 3 viên bi trắng có  

·       Cả hai bạn lấy ra 1 bi trắng và 2 bi đỏlà:  

·       Cả hai bạn lấy ra 2 bi trắng và 1 bi đỏ:   

Số kết quả thuận lợi là n(A)=3136+64+3136=6336

Xác suất biến cố  là : P(A) = 11/25

Chọn A.

Đáp án đúng: A

* Lời giải:

Số phần tử không gian mẫu: .

(chọn 3 đỉnh bất kì từ 12 đỉnh của đa giác ta được một tam giác)

Gọi A:  3 đỉnh được chọn tạo thành tam giác đều ”.

(Chia 12 đỉnh thành 3  phần. Mỗi phần gồm 4  đỉnh liên tiếp nhau. Mỗi đỉnh của tam giác đều ứng với một phần ở trên.Chỉ cần chọn 1 đỉnh thì 2 đỉnh còn lại xác định là duy nhất).

Ta có: .

Khi đó: .

* Phương pháp giải:

Tìm số phần tử không gian mẫu

- Tìm số phần tử thuận lợi của biến cố A đã cho

- Tính xác suất 

* Lý thuyết nắm thêm

1. Quy tắc cộng

- Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m + n cách thực hiện.

- Quy tắc cộng được phát biểu ở trên thực chất là quy tắc đếm số phần tử của hợp hai tập hợp hữu hạn không giao nhau, được phát biểu như sau:

Nếu A và B là các tập hợp hữu hạn và không giao nhau thì:

$n(A\cup B)=n\left(A\right)+n\left(B\right)$

- Chú ý: Quy tắc cộng có thể mở rộng cho nhiều hành động.

2. Quy tắc nhân

- Quy tắc nhân: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.

- Chú ý: Quy tắc nhân có thể mở rộng cho nhiều hành động liên liếp.

3. Hoán vị

3.1 Định nghĩa

- Định nghĩa: Cho tập hợp A gồm n phần tử (n ≥ 1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.

- Nhận xét: Hai hoán vị của n phần tử khác nhau ở thứ tự sắp xếp.

Chẳng hạn, hai hoán vị abc và cab của ba phần tử a; b; c là khác nhau.

3.2 Số các hoán vị

Kí hiệu: P_n là số các hoán vị của n phần tử.

- Định lí: P_n = n.(n – 1).(n – 2)….2.1

- Chú ý: Kí hiệu n.(n – 1)…2.1 là n! (đọc là n là giai thừa), ta có: P_n = n!.

4. Chỉnh hợp

4.1 Định nghĩa.

- Cho tập hợp A gồm n phần tử (n ≥ 1).

Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.

4.2 Số các chỉnh hợp

- Kí hiệu $A_n^k$ là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n) .

- Định lí:

$A_n^k=n(n-1)\mathrm{...}(n-k+\text{\hspace{0.17em}}1)$

5. Tổ hợp

5.1 Định nghĩa.

- Giả sử tập A có n phần tử (n ≥ 1). Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.

- Chú ý: Số k trong định nghĩa cần thỏa mãn điều kiện 1 ≤ k ≤ n. Tuy vậy, tập hợp không có phần tử nào là tập rỗng nên ta quy ước gọi tổ hợp chập 0 của n phần tử là tập rỗng.

- Ví dụ 4. Cho tập A = {3; 4; 5; 6}.

Ta liệt kê các tổ hợp chập 3 của A là: {3; 4; 5}; {3; 4; 6}; {3; 5; 6}; {4; 5; 6}.

5.2 Số các tổ hợp.

Kí hiệu $C_n^k$ là số các tổ hợp chập k của n phần tử ( 0 ≤ k ≤ n).

- Định lí: $C_n^k=\frac{n!}{k!(n-k)!}$.

5.3 Tính chất của các số $C_n^k$

a) Tính chất 1.

$C_n^k=C_n^{n-k};0\le k\le n$

Ví dụ 7. $C_8^4+C_8^5=C_9^5=126$.

6. Công thức nhị thức Niu- tơn

Ta có:

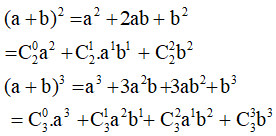
- Công thức nhị thức Niu – tơn.

$$\begin{gathered} {(a\text{\hspace{0.17em}\hspace{0.17em}}+b)}^n=C_n^0{a}^n+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^1.a^{n-1}b \\ +\text{\hspace{0.17em}}\mathrm{...}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^k.a^{n-k}{b}^k\text{\hspace{0.17em}}+\text{}\mathrm{....}+ \\ \text{}{C}_n^{n-1}a{b}^{n-1}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^n{b}^n \end{gathered}$$

- Hệ quả:

Với a = b = 1 ta có: $2^n=C_n^0+\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{...}\text{}+\text{\hspace{0.17em}}{C}_n^n$

Với a = 1; b = – 1 ta có: $0=C_n^0-\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{...}$$+\text{}{(-1)}^k.C_n^k+\text{}\mathrm{...}\text{}+{(-1)}^n\text{\hspace{0.17em}}{C}_n^n$

- Chú ý:

Trong biểu thức ở vế phải của công thức (1):

a) Số các hạng tử là n + 1.

b) Các hạng tử có số mũ của a giảm dần từ n đến 0; số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước $a^0=b^0=1$).

c) Các hệ số của mỗi cặp hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.

Xem thêm các bài viết liên quan hay, chi tiết:

Chuyên đề Ôn tập chương 2: Tổ hợp - xác suất - Toán 11 

Số phần tử của không gian mẫu là  .

Gọi A:”tổng số ghi trên 6 tấm thẻ ấy là một số lẻ”.

Từ 1 đến 11 có 6 số lẻ và 5 số chẵn.Để có tổng là một số lẻ ta có 3 trường hợp.

Trường hợp 1: Chọn được 1 thẻ mang số lẻ và 5 thẻ mang số chẵn có:  cách.

Trường hợp 2: Chọn được 3 thẻ mang số lẻ và 3 thẻ mang số chẵn có:  cách.

Trường hợp 2: Chọn được 5 thẻ mang số lẻ và 1 thẻ mang số chẵn có:  cách.

Do đó  n(A)=6+200+30=236

Vậy .

Chọn D.

Gọi X là biến cố: “có đúng 2 người bắn trúng đích “

·    Gọi A là biến cố: “người thứ nhất bắn trúng đích P(A)=0,8; $P\left(\overline{A}\right)=0,2$

    Gọi B là biến cố: “người thứ hai bắn trúng đích P(B)=0,6; $P\left(\overline{B}\right)=0,4$

·    Gọi C là biến cố: “người thứ ba bắn trúng đích P(C)=0,5; $P\left(\overline{C}\right)=0,5$

Ta thấy biến cố A, B, C là 3 biến cố độc lập nhau, theo công thức nhân xác suất ta có:

$P\left(X\right)=P(A.B.\overline{C})+P(A.\overline{B}.C)+P(\overline{A}.B.C)$=0,8.0,6.0,5+0,8.0,4.0,5+0,2.0,6.0,5=0,46

Chọn C.

Không gian mẫu là số cách chọn ngẫu nhiên 3 học sinh từ 13 học sinh.

Suy ra số phần tử của không gian mẫu là .

Gọi A là biến cố 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12

Ta có các trường hợp thuận lợi cho biến cố A là: 

                 ●   Trường hợp 1. Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có  cách.

                 ●   Trường hợp 2. Chọn 1 học sinh khối 11; 2 học sinh nữ khối 12 có  cách.

                 ●   Trường hợp 3. Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có  cách.

Suy ra số phần tử của biến cố A là 

Vậy xác suất cần tính 

Chọn D.

Không gian mẫu là số cách chọn ngẫu nhiên 6 viên bi từ hộp chứa 14 viên bi.

Suy ra số phần tử của không gian mẫu là  

Gọi A là biến cố 6 viên bi được lấy ra có đủ cả ba màu . Để tìm số phần tử của biến cố A ta đi tìm số phần tử của biến cố   tức là 6 viên bi lấy ra không có đủ ba màu như sau:

●   Trường hợp 1. Chọn 6 viên bi chỉ có một màu (chỉ chọn được màu vàng).

Do đó trường hợp này có  cách.

●   Trường hợp 2. Chọn 6 viên bi có đúng hai màu xanh và đỏ, có  cách.

Chọn 6 viên bi có đúng hai màu đỏ và vàng, có    cách.

Chọn 6 viên bi có đúng hai màu xanh và vàng, có   cách.

Do đó trường hợp này có  cách.

Suy ra số phần tử của biến cố   .

Suy ra số phần tử của biến cố A là

Vậy xác suất cần tính 

Chọn B.

Gọi A là biến cố "Động cơ I chạy tốt", B là biến cố "Động cơ II chạy tốt"

C là biến cố "Cả hai động cơ đều chạy tốt".

Ta thấy A, B là hai biến cố độc lập với nhau và C=A.B

Ta có P(C)=P(AB)=P(A).P(B)= 0,8 . 0,7 = 0,56

Chọn A.

Chọn C.

Gọi D là biến cố "Cả hai động cơ đều chạy không tốt".

Gọi A là biến cố động cơ I chạy tốt : P(A) = 0, 8 

Gọi B là biến cố động cơ II chạy tốt :  P(B) = 0,7

Ta thấy D=  $\overline{A} \overline{B}$ .

Hai biến cố $\overline{A}$ và $\overline{B}$ độc lập với nhau nên P(D=(1-P(A)). (1-P(B))=0,06.

 Gọi A là biến cố: động cơ I chạy tốt

Gọi B là  biến cố: động cơ II chạy tốt

Gọi K là biến cố "Có ít nhất một động cơ chạy tốt"

Biến cố đối:  $\overline{K }$: Cả hai động cơ không chạy tốt,

Hai biến cố A  và B độc lập với nhau nên: 

$$\begin{gathered} P\left(A\right) = 0, 8; P\left(B\right)= 0, 7 \\ P\left(\overline{A}\right)= 0, 2; P\left(\overline{B}\right) = 0,3 \\ P\left(\overline{K}\right) = P\left(\overline{A}\right). P\left(\overline{B}\right)= 0,2. 0,3 = 0,06 \end{gathered}$$

 Do đó ; P(K) = 1- 0, 06 = 0,94.

Chọn D.

Số cách lên toa của 7 người là: 

Ta tìm số khả năng thuận lợi của A như sau

 Chọn 3 toa có người lên: 

 Với toa có 4 người lên ta có:  cách chọn

 Với toa có 2 người lên ta có:  cách chọn

 Người cuối cùng cho vào toa còn lại nên có 1 cách

Theo quy tắc nhân ta có: 

Do đó: .

Chọn A.

Mỗi một cách lên toa thỏa yêu cầu bài toán chính là một hoán vị của 7 phần từ nên ta có: 

Do đó: 

Chọn D.

Gọi A_i là biến cố xuất hiện mặt i  chấm ( i=1;2;3;4;5;6)

Ta có  

Do

Gọi A là biến cố xuất hiện mặt chẵn, suy ra A = A₂ ∪ A₄ ∪ A₆

Vì các biến cố A_i  xung khắc nên:

Chọn A.

Không gian mẫu là số cách chọn ngẫu nhiên 7 hoa từ ba bó hoa gồm 21 hoa.

Suy ra số phần tử của không gian mẫu là .

Gọi A là biến cố “7 hoa được chọn có số hoa hồng bằng số hoa ly”. Ta có các trường hợp thuận lợi cho biến cố A  là:

               ●   Trường hợp 1. Chọn 1 hoa hồng, 1 hoa ly và 5 hoa huệ nên có  cách.

               ●   Trường hợp 2. Chọn 2 hoa hồng, 2 hoa ly và 3 hoa huệ nên có  cách.

               ●   Trường hợp 3. Chọn 3 hoa hồng, 3 hoa ly và 1 hoa huệ nên có  cách.

Suy ra số phần tử của biến cố A là .

Vậy xác suất cần tính 

Chọn D.

Chọn  A.