Giải bài tập trang 56 Chuyên đề Toán 10 Bài 2 - Cánh diều

Giải bài tập trang 56 Chuyên đề Toán 10 Bài 2 - Cánh diều

Bài 1 trang 56 Chuyên đề Toán 10:

Viết phương trình chính tắc của hypebol, biết:

a) Tiêu điểm là F₁(– 3; 0) và đỉnh là A₂ (2; 0).

b) Đỉnh là A₂(4; 0) và tiêu cự bằng 10.

c) Tiêu điểm F₂ (4; 0) và phương trình một đường tiệm cận là $y=-\frac{\sqrt{7}}{3}x$.

Lời giải:

a)

Gọi phương trình chính tắc của hypebol đã cho là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

+) Hypebol có một tiêu điểm là F₁(–3; 0) $\iff$ c = 3.

+) Hypebol có một đỉnh là A₂(2; 0) $\iff$ a = 2 $\iff$ b² = c² – a² = 3² – 2² = 5.

Vậy phương trình chính tắc của hypebol đã cho là hay $\frac{x^2}{4}-\frac{y^2}{5}=1.$

b)

Gọi phương trình chính tắc của hypebol đã cho là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

+) Hypebol có một đỉnh là A₂(4; 0) $\iff$ a = 4.

+) Hypebol có tiêu cự là 10 $\iff$ 2c = 10 $\iff$ c = 5 $\iff$ b² = c² – a² = 5² – 4² = 9.

Vậy phương trình chính tắc của hypebol đã cho là $\frac{x^2}{16}-\frac{y^2}{9}=1.$

c)

Gọi phương trình chính tắc của hypebol đã cho là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

+) Hypebol có một tiêu điểm là F₂(4; 0) $\iff$ c = 4.

+) Hypebol có một đường tiệm cận là $y=-\frac{\sqrt{7}}{3}x\Rightarrow$ $\frac{b}{a}=\frac{\sqrt{7}}{3}$

$$\begin{gathered} \Rightarrow \frac{a}{3}=\frac{b}{\sqrt{7}} \\ \Rightarrow \frac{a^2}{9}=\frac{b^2}{7}=\frac{a^2+b^2}{9+7}=\frac{c^2}{16}=\frac{4^2}{16}=1 \end{gathered}$$

 $\iff$ a² = 9, b² = 7.

Vậy phương trình chính tắc của hypebol đã cho là $\frac{x^2}{9}-\frac{y^2}{7}=1.$

Bài 2 trang 56 Chuyên đề Toán 10:

Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc $\frac{x^2}{4}-\frac{y^2}{1}=1$.

a) Xác định toạ độ các đỉnh, tiêu điểm, tiêu cự, độ dài trục thực của hypebol.

b) Xác định phương trình các đường tiệm cận của hypebol và vẽ hypebol trên.

Lời giải:

a) Ta có: a = 2, b = 1, c = $\sqrt{a^2+b^2}=\sqrt{5}.$

Toạ độ các đỉnh của hypebol là: A₁(–2; 0), A₂(2; 0).

Các tiêu điểm của hypebol là: F₁$\left(-\sqrt{5};0\right),$ F₂$\left(\sqrt{5};0\right),$

Tiêu cự của hypebol là: 2c = $2\sqrt{5}$

Độ dài trục thực của hypebol là: 2a = 4.

b) Phương trình các đường tiệm cận của hypebol là: $y=-\frac{b}{a}x=-\frac{1}{2}x$ và $y=\frac{b}{a}x=\frac{1}{2}x.$

Vẽ hypebol:

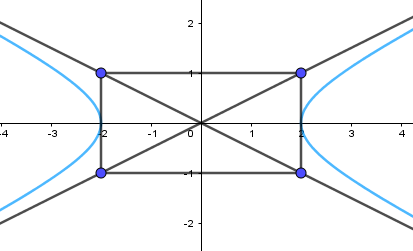
Bài 3 trang 56 Chuyên đề Toán 10:

Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc là x² – y² = 1. Chứng minh rằng hai đường tiệm cận của hypebol vuông góc với nhau.

Lời giải:

Ta có: a = 1, b = 1. Suy ra:

Phương trình hai đường tiệm cận của hypebol là: $d_1:y=-\frac{b}{a}x=-x$ và $d_2:y=\frac{b}{a}x=x.$

$d_1:y=-x$ hay x + y = 0 có vectơ pháp tuyến là $\overrightarrow{n_1}\left(1;1\right).$

$d_2:y=x$ hay x – y = 0 có vectơ pháp tuyến là $\overrightarrow{n_2}\left(1;-1\right).$

Có $\overrightarrow{n_1}.\overrightarrow{n_2}=1.1+1.\left(-1\right)=0.$ Suy ra hai vectơ này vuông góc với nhau, do đó hai đường thẳng d₁ và d₂ cũng vuông góc với nhau.

Bài 4 trang 56 Chuyên đề Toán 10:

Trong mặt phẳng tọa độ Oxy, cho hypebol $\left(H\right):\frac{x^2}{64}-\frac{y^2}{36}=1$. Lập phương trình chính tắc của elip (E), biết rằng (E) có các tiêu điểm là các tiêu điểm của (H) và các đỉnh của hình chữ nhật cơ sở của (H) đều nằm trên (E).

Lời giải:

Hypebol (H) có a = 8, b = 6 $\Rightarrow c=\sqrt{a^2+b^2}=10$ và một đỉnh của hình chữ nhật cơ sở là M(8; 6).

Gọi phương trình chính tắc của elip cần tìm là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).

Theo đề bài ta có:

+) (E) có các tiêu điểm là các tiêu điểm của (H)

$$\begin{gathered} \Rightarrow c=10 \\ \Rightarrow a^2-b^2=c^2=100\left(1\right). \end{gathered}$$

+) Các đỉnh của hình chữ nhật cơ sở của (H) đều nằm trên (E) 

$\Rightarrow M\left(8;6\right)\in \left(E\right)$

$$\begin{gathered} \Rightarrow \frac{8^2}{a^2}+\frac{6^2}{b^2}=1 \\ \Rightarrow \frac{64}{a^2}+\frac{36}{b^2}=1\left(2\right). \end{gathered}$$

Thế (1) vào (2) ta được:

$$\begin{gathered} \frac{64}{b^2+100}+\frac{36}{b^2}=1 \\ \Rightarrow \frac{64b^2+36\left(b^2+100\right)}{\left(b^2+100\right)b^2}=1 \end{gathered}$$

$\Rightarrow 64b^2+36\left(b^2+100\right)=\left(b^2+100\right)b^2$

$$\begin{gathered} \Rightarrow 100b^2+3600=b^4+100b^2 \\ \Rightarrow b^4=3600\Rightarrow b^2=60 \\ \Rightarrow a^2=160. \end{gathered}$$

Vậy phương trình chính tắc của elip cần tìm là $\frac{x^2}{160}+\frac{y^2}{60}=1.$ 

Bài 5 trang 56 Chuyên đề Toán 10:

Dọc theo bờ biển, người ta thiết lập hệ thống định vị vô tuyến dẫn đường tầm xa để truyền tín hiệu cho máy bay hoặc tàu thuỷ hoạt động trên biển. Trong hệ thống đó có hai đài vô tuyến đặt lần lượt tại địa điểm A và địa điểm B, khoảng cách AB = 650 km (Hình 18). Giả sử có một con tàu chuyển động trên biển với quỹ đạo là hypebol nhận A và B là hai tiêu điểm.

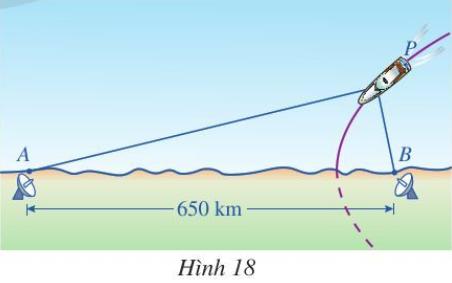
Khi đang ở vị trí P, máy thu tín hiệu trên con tàu chuyển đổi chênh lệch thời gian nhận các tín hiệu từ A và B thành hiệu khoảng cách |PA – PB|. Giả sử thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A là 0,0012 s. Vận tốc di chuyển của tín hiệu là 3 . 10⁸ m/s.

a) Lập phương trình hypebol mô tả quỹ đạo chuyển động của con tàu.

b) Chứng tỏ rằng tại mọi thời điểm trên quỹ đạo chuyển động thì thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A luôn là 0,0012 s.

Lời giải:

a) Vì thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A là 0,0012 s nên tại thời điểm đó PB – PA = (3 . 10⁸) . 0,0012 = 360000 (m) = 360 (km).

Vì con tàu chuyển động với quỹ đạo là hypebol nhận A và B là hai tiêu điểm nên |PA – PB| = 360 (km) với mọi vị trí của P.

Chọn hệ trục toạ độ sao cho gốc toạ độ trùng với trung điểm của AB và trục Ox trùng với AB, đơn vị trên hai trục là km thì hypebol này có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

Vì |PA – PB| = 360 nên 2a = 360, suy ra a =180.

Theo đề bài, AB = 650, suy ra 2c = 650, suy ra c = 325.

b² = c² – a² = 325² – 180² = 73225.

Vậy phương trình hypebol mô tả quỹ đạo chuyển động của con tàu là $\frac{x^2}{32400}-\frac{y^2}{73225}=1.$

b) Vì con tàu chỉ chuyển động ở nhánh bên phải trục Oy của hypebol nên ta PB < PA với mọi vị trí của P. Do đó tàu luôn nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A.

Gọi t₁ là thời gian để tàu nhận được tín hiệu từ A, t₂ là thời gian để tàu nhận được tín hiệu từ B thì $t_1=\frac{PA}{v},t_2=\frac{PB}{v}$ với v là vận tốc di chuyển của tín hiệu.

Khi đó, ta có:

t₁ – t₂ = $\frac{PA-PB}{v}=\frac{360000}{3.8^{10}}=0,0012\left(s\right).$

Vậy thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A luôn là 0,0012 s.

Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Cánh diều hay, chi tiết khác:

Giải bài tập trang 49 Chuyên đề Toán 10 Bài 2

Giải bài tập trang 50, 51 Chuyên đề Toán 10 Bài 2

Giải bài tập trang 52 Chuyên đề Toán 10 Bài 2

Giải bài tập trang 53, 54 Chuyên đề Toán 10 Bài 2

Giải bài tập trang 55 Chuyên đề Toán 10 Bài 2