Giải bài tập trang 38 Chuyên đề Toán 10 Bài 2 - Cánh diều
Với Giải bài tập trang 38 Chuyên đề Toán 10 trong Bài 2: Nhị thức newton sách Chuyên đề Toán lớp 10 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Chuyên đề Toán 10 trang 38.
Giải bài tập trang 38 Chuyên đề Toán 10 Bài 2 - Cánh diều
Bài 7 trang 38 Chuyên đề Toán 10:
Tìm hệ số lớn nhất trong khai triển của:
a) (a + b)8;
b) (a + b)9.
Lời giải:
Vì dãy hệ số của khai triển (a + b)n tăng dần đến "giữa" rồi giảm dần nên:
a) Hệ số lớn nhất của (a + b)8 là
b) Hệ số lớn nhất của (a + b)9 là và
Bài 8 trang 38 Chuyên đề Toán 10:
Chứng minh công thức nhị thức Newton bằng phương pháp quy nạp:
với n ℕ*.
Lời giải:
+) Với n = 1, ta có: (a + b)1 = a + b =
Vậy công thức đúng với n = 1.
+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh công thức cũng đúng với k + 1, tức là:
Thật vậy, theo giả thiết quy nạp ta có:
Khi đó:
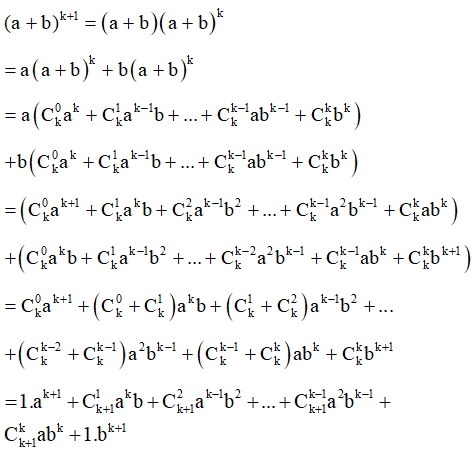
(vì , i ℕ, k ℕ*)
Vậy công thức cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, công thức đã cho đúng với mọi n ℕ*.
Bài 9 trang 38 Chuyên đề Toán 10:
Bằng phương pháp quy nạp, chứng minh:
a) n5 – n chia hết cho 5 n ℕ*;
b) n7 – n chia hết cho 7 n ℕ*.
Lời giải:
a)
+) Với n = 1, ta có: 15 – 1 = 0 ⁝ 5.
Vậy mệnh đề đúng với n = 1.
+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: (k + 1)5 – (k + 1) ⁝ 5.
Thật vậy, theo giả thiết quy nạp ta có: k5 – k ⁝ 5.
Khi đó:
(k + 1)5 – (k + 1)
Mà và đều chia hết cho 5, do đó
⁝ 5 hay (k + 1)5 – (k + 1) ⁝ 5.
Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ℕ*.
b)
+) Với n = 1, ta có: 17 – 1 = 0 ⁝ 7.
Vậy mệnh đề đúng với n = 1.
+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: (k + 1)7 – (k + 1) ⁝ 7.
Thật vậy, theo giả thiết quy nạp ta có: k7 – k ⁝ 7.
Khi đó:
(k + 1)7 – (k + 1)
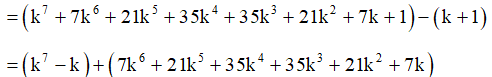
Mà và đều chia hết cho 7, do đó
⁝ 7 hay (k + 1)7 – (k + 1) ⁝ 7.
Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ℕ*.
Bài 10 trang 38 Chuyên đề Toán 10:
Cho tập hợp A = {x1; x2; x3; ... ; xn} có n phần tử. Tính số tập hợp con của A.
Lời giải:
Vì A có n phần tử nên số tập hợp con có k phần tử của tập hợp A là:
Như vậy tổng số tập con của tập hợp A là:
Lại có (theo luyện tập 2).
Vậy tập hợp A có tất cả 2n tập con.
Bài 11 trang 38 Chuyên đề Toán 10:
Một nhóm gồm 10 học sinh tham gia chiến dịch Mùa hè xanh. Nhà trường muốn chọn ra một đội công tác có ít nhất hai học sinh trong những học sinh trên. Hỏi có bao nhiêu cách lập đội công tác như thế?
Lời giải:
Đội công tác có thể có từ 2 đến 10 học sinh.
Nếu đội công tác có k học sinh thì ta có cách chọn.
Như vậy tổng số cách chọn là:
Lại có (áp dụng luyện tập 2 với n = 10).
.
Vậy có 1013 cách.
Bài 12 trang 38 Chuyên đề Toán 10:
Để tham gia một cuộc thi làm bánh, bạn Tiến làm 12 chiếc bánh có màu khác nhau và chọn ra số nguyên dương chẵn chiếc bánh để cho vào một hộp trưng bày. Hỏi bạn Tiến có bao nhiêu cách để chọn bánh cho vào hộp trưng bày đó?
Lời giải:
Số bánh bạn Tiến có thể chọn để cho vào hộp có thể là 2, 4, 6, 8, 10 hoặc 12.
Như vậy tổng số cách chọn là:
Lại có
(áp dụng câu c Ví dụ 3 với n = 6).
.
Vậy có 2047 cách.
Bài 13 trang 38 Chuyên đề Toán 10:
Bác Thành muốn mua quà cho con nhân dịp sinh nhật nên đã đến một cửa hàng đồ chơi. Bác dự định chọn một trong năm loại đồ chơi. Ở cửa hàng, mỗi loại đồ chơi đó chỉ có 10 sản phẩm khác nhau bày bán. Biết rằng nếu mua bộ trực thăng điều khiển từ xa, bác sẽ chỉ mua 1 sản phẩm; nếu mua bộ đồ chơi lego, bác sẽ mua 3 sản phẩm khác nhau; nếu mua bộ lắp ghép robot chạy bằng năng lượng mặt trời, bác sẽ mua 5 sản phẩm khác nhau; nếu mua rubik, bác sẽ mua 7 sản phẩm khác nhau; còn nếu mua mô hình khủng long, bác sẽ mua 9 sản phẩm khác nhau. Bác Thành có bao nhiêu cách chọn quà sinh nhật cho con?
Lời giải:
Số cách chọn nếu bác Thành mua:
– Bộ trực thăng điều khiển từ xa là:
– Bộ đồ chơi lego là:
– Bộ lắp ghép robot chạy bằng năng lượng mặt trời là:
– Rubik là:
– Mô hình khủng long là:
Vậy tổng số cách chọn là:
Lại có
(áp dụng câu c Ví dụ 3 với n = 5).
Vậy có 512 cách.
Bài 14 trang 38 Chuyên đề Toán 10:
Giả sử tính trạng ở một loài cây được quy định do tác động cộng gộp của n cặp alen phân li độc lập A1a1, A2a2, ..., Anan. Cho cây F1 dị hợp về n cặp alen giao phối với nhau. Tỉ lệ phân li kiểu hình của F2 là hệ số của khai triển nhị thức Newton (a + b)2n, nghĩa là tỉ lệ phân li kiểu hình của F2 là
Cho biết một loài cây có tính trạng được quy định bởi tác động cộng gộp của 4 cặp alen phân li độc lập. Tìm tỉ lệ phân li kiểu hình của F2 nếu cây F1 dị hợp về 4 cặp alen giao phối với nhau.
Lời giải:
Thay n = 4 vào công thức trong đề bài, ta được:
Tỉ lệ phân li kiểu hình của F2 nếu cây F1 dị hợp về 4 cặp alen giao phối với nhau là:
hay
Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Cánh diều hay, chi tiết khác:
Giải bài tập trang 31, 32 Chuyên đề Toán 10 Bài 2
Giải bài tập trang 33, 34 Chuyên đề Toán 10 Bài 2
Giải bài tập trang 35 Chuyên đề Toán 10 Bài 2
Giải bài tập trang 36 Chuyên đề Toán 10 Bài 2
Giải bài tập trang 37 Chuyên đề Toán 10 Bài 2
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Bố cục tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Soạn văn lớp 10 (ngắn nhất) – Cánh Diều
- Giải sbt Ngữ văn lớp 10 – Cánh Diều
- Văn mẫu lớp 10 – Cánh Diều
- Giải Chuyên đề học tập Ngữ văn 10 – Cánh diều
- Giải sgk Tiếng Anh 10 – Explore new worlds
- Giải sgk Tiếng Anh 10 – ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 10 ilearn Smart World đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 i-learn Smart World
- Giải sbt Tiếng Anh 10 - iLearn Smart World
- Giải sgk Vật lí 10 – Cánh Diều
- Giải sbt Vật lí 10 – Cánh Diều
- Lý thuyết Vật lí 10 – Cánh Diều
- Giải Chuyên đề Vật lí 10 – Cánh Diều
- Giải sgk Hóa học 10 – Cánh Diều
- Lý thuyết Hóa học 10 – Cánh Diều
- Giải sbt Hóa học 10 – Cánh Diều
- Giải Chuyên đề Hóa học 10 – Cánh Diều
- Giải sgk Sinh học 10 – Cánh Diều
- Giải sbt Sinh học 10 – Cánh Diều
- Lý thuyết Sinh học 10 – Cánh Diều
- Giải Chuyên đề Sinh học 10 – Cánh diều
- Giải sgk Lịch sử 10 – Cánh Diều
- Giải sbt Lịch sử 10 – Cánh Diều
- Giải Chuyên đề Lịch sử 10 – Cánh Diều
- Lý thuyết Lịch sử 10 – Cánh diều
- Giải sgk Địa lí 10 – Cánh Diều
- Lý thuyết Địa Lí 10 – Cánh Diều
- Giải sbt Địa lí 10 – Cánh Diều
- Giải Chuyên đề Địa lí 10 – Cánh Diều
- Lý thuyết Công nghệ 10 – Cánh Diều
- Giải sgk Công nghệ 10 – Cánh Diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải Chuyên đề Kinh tế pháp luật 10 – Cánh diều
- Lý thuyết KTPL 10 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 10 – Cánh Diều
- Giải sgk Giáo dục quốc phòng - an ninh 10 – Cánh diều
- Giải sbt Giáo dục quốc phòng - an ninh 10 – Cánh Diều
- Giải sgk Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sbt Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sgk Tin học 10 – Cánh Diều
- Giải sbt Tin học 10 – Cánh Diều
- Giải Chuyên đề Tin học 10 – Cánh diều
- Lý thuyết Tin học 10 - Cánh diều
- Giải sgk Giáo dục thể chất 10 – Cánh Diều
