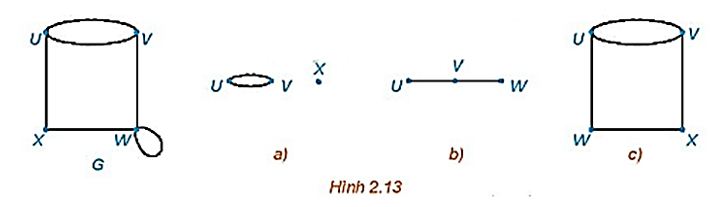Chuyên đề Toán 11 Bài 8 (Kết nối tri thức): Một vài khái niệm cơ bản

Giải Chuyên đề Toán 11 Bài 8: Một vài khái niệm cơ bản

Mở đầu trang 34 Chuyên đề Toán 11: Trước khi vào một hồi nghị, các đại biểu bắt tay nhau (hai người bắt tay nhau nhiều nhất 1 lần). Có một đại biểu không bắt tay ai hết và thấy rằng có 4 người bắt tay 4 lần, 5 người bắt tay 5 lần và 6 người bắt tay 6 lần. Nếu hội nghị có đúng 16 đại biểu thì ông ta đếm nhầm. Vì sao có thể kết luận như vậy?

Lời giải:

Những kiến thức ban đầu về lí thuyết đồ thị trong bài học này sẽ giúp chúng ta tìm được câu trả lời cho tình huống trên như sau:

Ta vẽ một đồ thị với 16 đỉnh tương ứng với 16 đại biểu tham dự hội nghị. Nếu hai đại biểu nào bắt tay nhau thì ta nối hai đỉnh tương ứng bằng một cạnh.

Theo số liệu mà đại biểu đếm số bắt tay cung cấp, ta có một đồ thị với 16 đỉnh, trong đó có 1 đỉnh bậc 0, 4 đỉnh bậc 4, 5 đỉnh bậc 5 và 6 đỉnh bậc 6.

Ở đây số đỉnh bậc 5 là 5, là một số lẻ. Điều này mâu thuẫn với hệ quả của Định lí bắt tay (Số đỉnh bậc lẻ của mọi đồ thị là một số chẵn).

Vậy đại biểu đó đã đếm sai.

1. Đồ thị

HĐ1 trang 35 Chuyên đề Toán 11: Nhận biết khái niệm đồ thị

Có bốn bạn học sinh khối 11 là An, Bình, Cường và Dung, trong đó: An là bạn của Bình và Cường, nhưng không là bạn của Dung; Dung là bạn của Cường, nhưng không là bạn của Bình; Bình là bạn của Cường.

a) Hãy biểu diễn mỗi bạn An, Bình, Cường, Dung bằng một điểm trên mặt phẳng và dùng chữ cái đầu (in hoa) trong tên của họ để đặt tên cho các điểm này.

b) Nếu hai người là bạn của nhau, hãy nối các điểm biểu diễn tương ứng bằng một đoạn thẳng (hay đoạn đường cong).

c) Từ hình vẽ thu được ở HĐ1b, hãy cho biết: ai có nhiều bạn nhất và ai có ít bạn nhất?

Lời giải:

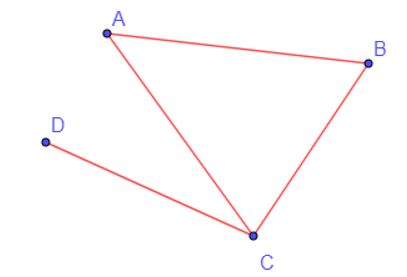
a) Lần lượt biểu diễn mỗi bạn An, Bình, Cường, Dung bằng các điểm A, B, C, D trên mặt phẳng (hình vẽ).

b) Nếu hai người là bạn của nhau, nối các điểm biểu diễn tương ứng (hình vẽ).

 c) Từ hình vẽ thu được, ta thấy Cường có nhiều bạn nhất vì từ điểm C đều có đoạn thẳng nối tới cả 3 điểm A, B, D và Dung có ít bạn nhất vì từ điểm D chỉ có 1 đoạn thẳng nối đến điểm C.

Luyện tập 1 trang 36 Chuyên đề Toán 11: Bảng F của giải vô địch bóng đá thế giới World Cup 2018 gồm bốn đội: Đức, Hàn Quốc, Mexico và Thuỵ Điển. Biểu diễn các đội này bằng các điểm phân biệt kí hiệu lần lượt là D, H, M, T (vẽ sao cho không có ba điểm nào thẳng hàng để dễ quan sát) và nếu hai đội nào đấu với nhau thì ta nối hai điểm tương ứng bằng một đoạn thẳng, ta sẽ được một đồ thị G.

Viết tập hợp các đỉnh và tập hợp các cạnh của đồ thị G.

Lời giải:

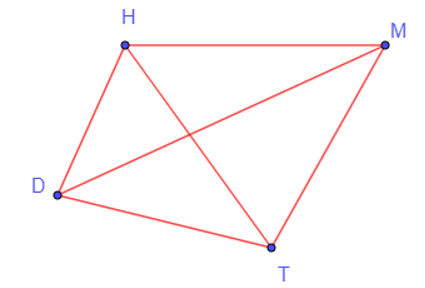
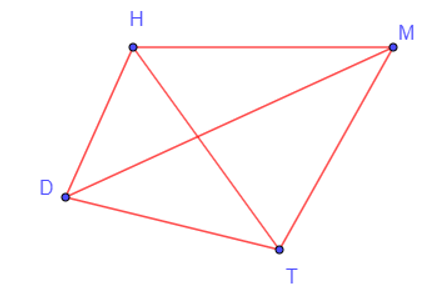
Trong một bảng đấu, các đội sẽ thi đấu vòng tròn, có nghĩa là mỗi một đội sẽ lần lượt thi đấu với ba đội còn lại. Do đó, từ mỗi điểm D, H, M, T, ta vẽ các đoạn thẳng đến các điểm còn lại ta được đồ thị G như hình vẽ dưới đây.

Khi đó ta có: V(G) = {D; H; M; T}.

E(G) = {DH; DT; DM; HT; HM; MT}.

HĐ2 trang 36 Chuyên đề Toán 11: Nhận biết khái niệm đơn đồ thị

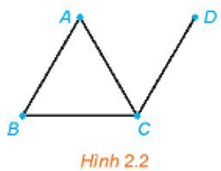
Xét đồ thị cho trong Hình 2.2.

a) Đồ thị trên có khuyên không?

b) Có hai đỉnh nào của đồ thị được nối với nhau bằng nhiều hơn một cạnh không?

Lời giải:

a) Đồ thị trên không có khuyên vì không có cạnh nào có hai đầu mút trùng nhau tại một đỉnh.

b) Không có hai đỉnh nào của đồ thị được nối với nhau bằng nhiều hơn một cạnh.

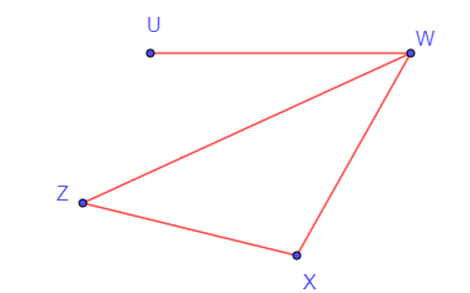
Luyện tập 2 trang 36 Chuyên đề Toán 11: Vẽ đồ thị G với các đỉnh và các cạnh như sau:

V(G) = {U, W, X, Z} và E(G) = {UW, WX, WZ, XZ}.

G có phải là một đơn đồ thị không?

Lời giải:

G là một đơn đồ thị, do hai đỉnh bất kì đều nối với nhau bởi không quá một cạnh.

HĐ3 trang 36 Chuyên đề Toán 11: Nhận biết đồ thị đầy đủ

Xét đồ thị nhận được trong Luyện tập 1. Có cặp đỉnh nào của đồ thị này mà không có cạnh nào nối chúng không?

Lời giải:

Quan sát đồ thị có được từ Luyện tập 1, ta thấy không có bất kì cặp đỉnh nào của đồ thị mà không có cạnh nối chúng với nhau hay mỗi cặp đỉnh của đồ thị đều được nối với nhau bằng một cạnh.

Luyện tập 3 trang 37 Chuyên đề Toán 11: Vẽ các đồ thị đầy đủ có 5 đỉnh, có 6 đỉnh.

Lời giải:

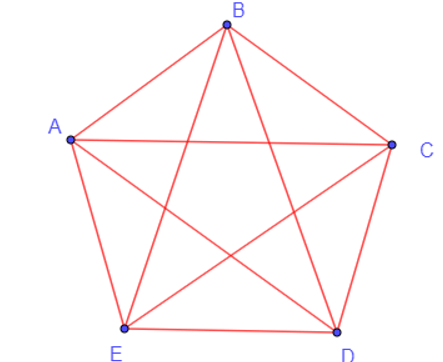
+) Đồ thị đầy đủ có 5 đỉnh:

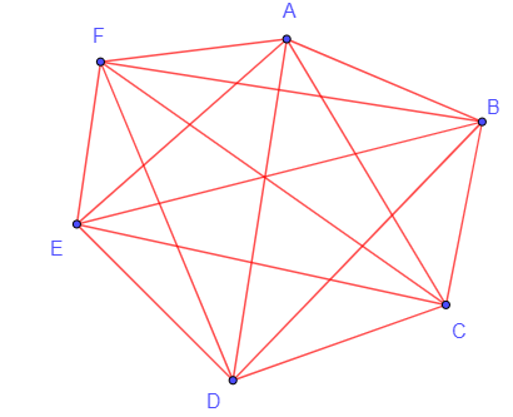
+) Đồ thị đầy đủ có 6 đỉnh:

2. Bậc của đỉnh

HĐ4 trang 37 Chuyên đề Toán 11: Nhận biết bậc của đỉnh

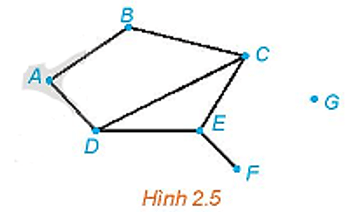
Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.

Lời giải:

Đỉnh là đầu mút của 0 cạnh là đỉnh G.

Đỉnh là đầu mút của 1 cạnh là đỉnh F.

Các đỉnh là đầu mút của 2 cạnh là các đỉnh A, B.

Các đỉnh là đầu mút của 3 cạnh là các đỉnh C, D, E.

Luyện tập 4 trang 38 Chuyên đề Toán 11: Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 4.

Lời giải:

Giả sử có đồ thị thỏa mãn yêu cầu bài toán. Gọi x là số đỉnh bậc 3 của đồ thị.

Khi đó, ta có số đỉnh bậc 4 là: 12 – x.

Tổng số bậc của các đỉnh là: 3x + 4(12 – x).

Vì đồ thị có 28 cạnh nên theo Định lí bắt tay thì đồ thị có tổng số bậc là 28 . 2 = 56.

Do đó, ta có phương trình 3x + 4(12 – x) = 56, tức là 8 + x = 0. Phương trình này không có nghiệm là số tự nhiên, do đó không tồn tại đồ thị thỏa mãn điều kiện đề bài.

3. Đường đi và chu trình

HĐ5 trang 38 Chuyên đề Toán 11: Nhận biết khái niệm đường đi và chu trình

Cho đồ thị như Hình 2.7. Bằng cách đi dọc theo các cạnh, với điều kiện không đi qua cạnh nào quá một lần (có thể có cạnh không cần đi qua), hãy chỉ ra các cách để:

a) Đi từ đỉnh A đến đỉnh E.

b) Đi từ đỉnh A và lại quay về đỉnh A.

Lời giải:

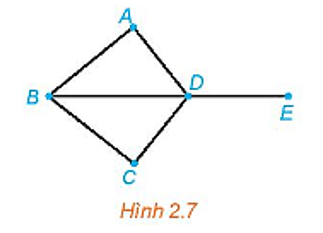
a) Để đi từ đỉnh A đến đỉnh E ta có thể di chuyển theo con đường từ A đến D rồi từ D đến E (hoặc cũng có thể chọn các con đường khác, chẳng hạn đi theo đường từ A đến B rồi từ B đến D và từ D đến E, ...)

b) Để đi từ đỉnh A và lại quay về đỉnh A ta có thể di chuyển theo con đường từ A đến D rồi từ D đến B và từ B quay lại A (tương tự cũng có thể chọn các con đường khác).

Luyện tập 5 trang 39 Chuyên đề Toán 11: Cho đồ thị đầy đủ có 5 đỉnh như Hình 2.9. Tìm những chu trình sơ cấp xuất phát từ đỉnh A và có: độ dài 4; độ dài 5.

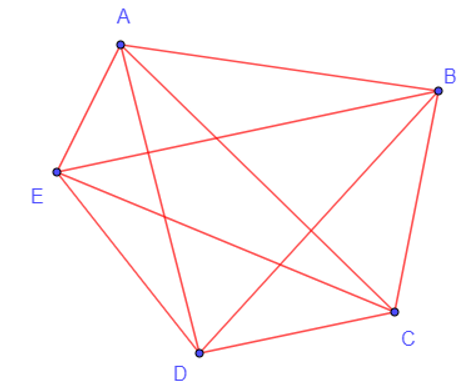
Lời giải:

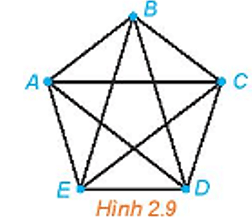
Những chu trình sơ cấp có độ dài 4 xuất phát từ đỉnh A là: ABCDA, ABCEA, ABDCA, ABDEA, ABEDA, ABECA, ACBDA, ACBEA, ACDBA, ACDEA, ACEBA, ACEDA, ADBEA, ADBCA, ADCEA, ADCBA, ADEBA, ADECA, AEBDA, AEBCA, AECDA, AEDCA, AECBA, AEDBA.

Những chu trình sơ cấp có độ dài 5 xuất phát từ đỉnh A là: ABCDEA, ABCEDA, ABECDA, ABEDCA, ABDCEA, ABDECA, ACBEDA, ACBDEA, ACDEBA, ACDBEA, ACEDBA, ACEBDA, ADBECA, ADBCEA, ADCBEA, ADCEBA, ADECBA, ADEBCA, AECDBA, AECBDA, AEDCBA, AEDBCA, AEBCDA, AEBDCA.

HĐ6 trang 39 Chuyên đề Toán 11: Nhận biết tính liên thông của đồ thị

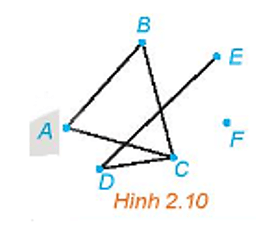
Trong đồ thị ở Hình 2.10, hãy:

a) Tìm một đường đi từ đỉnh A đến đỉnh E.

b) Có tồn tại một đường đi từ đỉnh A đến đỉnh F hay không?

Lời giải:

a) Một đường đi từ đỉnh A đến đỉnh E là ABCDE.

b) Không tồn tại một đường đi từ đỉnh A đến đỉnh F.

Luyện tập 6 trang 40 Chuyên đề Toán 11: Chứng minh đồ thị ở Hình 2.12 là liên thông. Hãy chỉ ra một đường đi nối đỉnh 1 và đỉnh 6.

Lời giải:

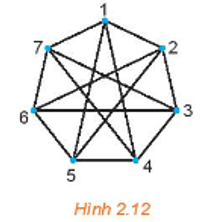
Đồ thị Hình 2.12 có 7 đỉnh, lấy 2 đỉnh bất kì của đồ thị, ta đều thấy có một đường đi nối hai điểm đó, do đó mọi cặp đỉnh của đồ thị này đều liên thông nên đồ thị này liên thông.

Bài tập

Bài 2.1 trang 40 Chuyên đề Toán 11: Vẽ hình biểu diễn của đồ thị G với tập đỉnh V(G) = {1; 2; 3; 4; 5} và tập cạnh

E(G) = {12; 14; 23; 25; 34; 35}.

Đồ thị G có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?

Lời giải:

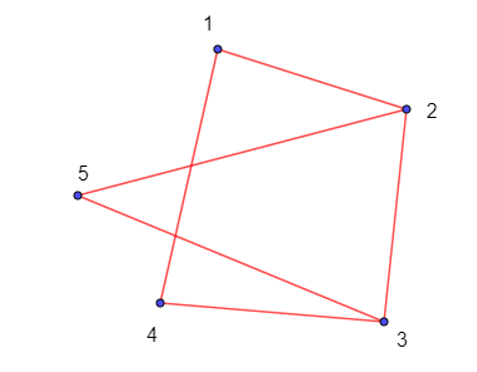
Hình biểu diễn của đồ thị G như sau.

Đồ thị G là đơn đồ thị, nhưng không phải đồ thị đầy đủ.

Bài 2.2 trang 40 Chuyên đề Toán 11: Hãy vẽ một đồ thị có 4 đỉnh và:

a) có đúng hai đỉnh cùng bậc và bậc là 1;

b) có đúng hai đỉnh cùng bậc và bậc là 2.

Lời giải:

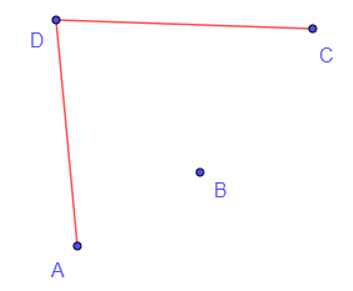
a) Đồ thị có 4 đỉnh và có đúng hai đỉnh cùng bậc và bậc là 1.

Ở đây, đỉnh A và C đều có bậc 1, trong khi đỉnh D có bậc 2, còn đỉnh B có bậc 0.

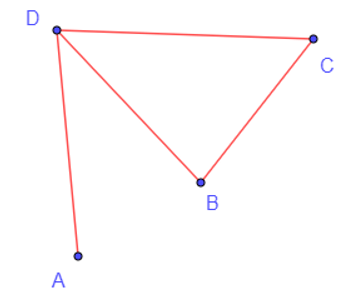
b) Đồ thị có 4 đỉnh và có đúng hai đỉnh cùng bậc và bậc là 2.

Ở đây, đỉnh B và C đều có bậc 2, trong khi đỉnh D có bậc 3, còn đỉnh A có bậc 1.

Bài 2.3 trang 40 Chuyên đề Toán 11: Một đồ thị con của đồ thị G là một đồ thị mà mọi đỉnh của nó đều là đỉnh của G và mọi cạnh của nó cũng là cạnh của G.

Những đồ thị nào trong các hình a), b), c) dưới đây là đồ thị con của đồ thị G?

Lời giải:

Các đồ thị a) và c) là đồ thị con của đồ thị G vì mọi đỉnh và mọi cạnh của từng đồ thị a) và c) đều là đỉnh và cạnh của G.

Đồ thị b) không phải là đồ thị con của đồ thị G vì đồ thị b) chứa cạnh UW không phải là cạnh của G.

Bài 2.4 trang 40 Chuyên đề Toán 11: Chứng minh rằng một đồ thị đầy đủ có n đỉnh thì có $\frac{n\left(n-1\right)}{2}$ cạnh.

Lời giải:

Do đồ thị đầy đủ nên mỗi đỉnh được nối với n – 1 đỉnh khác, tức là số cạnh là n(n – 1) cạnh.

Tuy nhiên, do ở trên ta đã tính lặp một cạnh 2 lần, nên số cạnh thực tế của đồ thị là $\frac{n\left(n-1\right)}{2}$.

Bài 2.5 trang 40 Chuyên đề Toán 11: Chứng minh rằng không tồn tại đồ thị với các đỉnh có bậc là 2, 3, 3, 4, 4 và 5. 

Lời giải:

Ta thấy đồ thị đưa ra ở đề bài có 3 đỉnh bậc lẻ (3, 3 và 5), nên theo Hệ quả của Định lí bắt tay, không có đồ thị nào thỏa mãn điều kiện đưa ra.

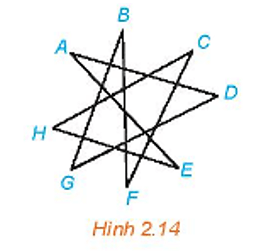
Bài 2.6 trang 40 Chuyên đề Toán 11: Cho đồ thị G như Hình 2.14.

a) Tìm một đường đi từ đỉnh A đến đỉnh B.

b) G có liên thông không?

c) Trong G có chu trình sơ cấp nào không?

Lời giải:

a) Một đường đi từ đỉnh A đến đỉnh B là: ADGB.

b) Ta thấy hai đỉnh bất kì của đồ thị đều liên thông (tức là đều có đường đi nối chúng), nên G liên thông.

c) Chu trình sơ cấp trong G là: AEHCFBGDA.

Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 7: Phép đồng dạng

Bài tập cuối chuyên đề 1

Bài 9: Đường đi Euler và đường đi Hamilton

Bài 10: Bài toán tìm đường tối ưu trong một vài trường hợp đơn giản

Bài tập cuối chuyên đề 2