Chuyên đề Toán 11 Bài 6 (Kết nối tri thức): Phép vị tự

Giải Chuyên đề Toán 11 Bài 6: Phép vị tự

1. Phép vị tự

HĐ1 trang 26 Chuyên đề Toán 11: Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.

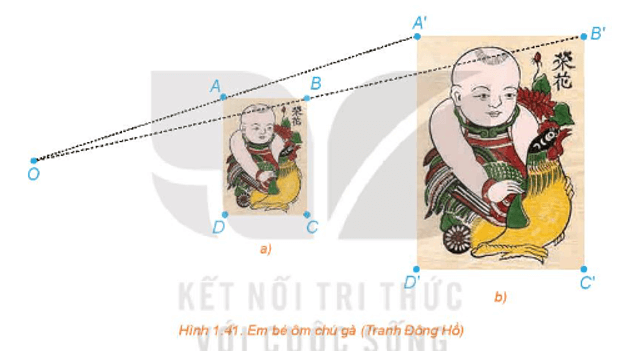
a) Giải thích vì sao các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.

b) Hãy tính các tỉ số $\frac{OA}{OA\text{'}},\frac{OB}{OB\text{'}},\frac{OC}{OC\text{'}},\frac{OD}{OD\text{'}}$.

c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?

Lời giải:

a) Gọi O là giao điểm của AA' và BB'.

Xét tam giác OA'B' có AB // A'B', theo định lý Thales, ta có:

$\frac{OA}{OA\text{'}}=\frac{OB}{OB\text{'}}=\frac{AB}{A\text{'}B\text{'}}=\frac{1}{2}$.

Từ đó suy ra A, B lần lượt là trung điểm của OA' và OB'.

Gọi C" là giao điểm của BC và OC'. Vì BC // B'C' nên BC" // B'C'.

Xét tam giác OB'C' có BC" // B'C' và B là trung điểm của OB' nên BC" là đường trung bình của tam giác OB'C'. Suy ra BC" = $\frac{1}{2}$B'C' và C" là trung điểm của OC'.

Mặt khác theo giả thiết ta có BC = $\frac{1}{2}$B'C'. Do vậy C" trùng với C và C là trung điểm của OC'.

Chứng minh tương tự, ta được D là trung điểm của OD'.

Vậy các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.

b) Vì A, B, C, D lần lượt là trung điểm của OA', OB', OC', OD' nên

$\frac{OA}{OA\text{'}}=\frac{OB}{OB\text{'}}=\frac{OC}{OC\text{'}}=\frac{OD}{OD\text{'}}=\frac{1}{2}$.

c) Dùng thước thẳng nối hai điểm tương ứng trên hai bức tranh, cụ thể, đầu mỏ trên của chú gà ở hai bức tranh, ta thấy đường thẳng này đi qua điểm O.

Câu hỏi trang 27 Chuyên đề Toán 11: Phép vị tự V_{(O, k)­} biến điểm O thành điểm nào? Nếu phép vị tự V_{(O, k)} biến điểm M thành điểm M' thì phép vị tự $V_{\left(O,\frac{1}{k}\right)}$ biến điểm M' thành điểm nào?

Lời giải:

- Phép vị tự V_{(O, k)} biến điểm O thành điểm O.

- Nếu phép vị tự V_{(O, k)} biến điểm M thành điểm M' thì phép vị tự $V_{\left(O,\frac{1}{k}\right)}$ biến điểm M' thành điểm M.

Thật vậy, nếu M' là ảnh M qua phép vị tự V_{(O, k)} thì $\overrightarrow{OM\text{'}}=k\overrightarrow{OM}\iff \overrightarrow{OM}=\frac{1}{k}\overrightarrow{OM\text{'}}$. Điều này có nghĩa là M là ảnh của M' qua phép vị tự $V_{\left(O,\frac{1}{k}\right)}$.

Luyện tập 1 trang 27 Chuyên đề Toán 11: Chứng minh rằng, phép vị tự V_{(O, 1)} là phép đồng nhất, phép vị tự V_{(o, – 1)} là phép đối xứng tâm O.

Lời giải:

+ Phép vị tự V_{(O, 1)} biến điểm M thành điểm M' thỏa mãn $\overrightarrow{OM\text{'}}=\overrightarrow{OM}$. Khi đó M' trùng với M. Do đó, phép vị tự V_{(O, 1)} là phép đồng nhất.

+ Phép vị tự V_{(O, – 1)} biến điểm M thành điểm M" thỏa mãn $\overrightarrow{OM"}=-\overrightarrow{OM}$. Khi đó O là trung điểm của MM". Do đó, M" là ảnh của M qua phép đối xứng tâm O hay phép vị tự V_{(O, – 1)} là phép đối xứng tâm O.

Vận dụng 1 trang 27 Chuyên đề Toán 11: Quan sát hai bức tranh em bé ôm chú gà ở phần mở đầu bài học và chỉ ra phép vị tự biến bức tranh nhỏ thành bức tranh lớn và phép vị tự biến bức tranh lớn thành bức tranh nhỏ.

Lời giải:

Ta có: $\frac{OA}{OA\text{'}}=\frac{OB}{OB\text{'}}=\frac{OC}{OC\text{'}}=\frac{OD}{OD\text{'}}=\frac{1}{2}$ (theo HĐ1).

Suy ra $\overrightarrow{OA\text{'}}=2\overrightarrow{OA};\overrightarrow{OB\text{'}}=2\overrightarrow{OB};\overrightarrow{OC\text{'}}=2\overrightarrow{OC};\overrightarrow{OD\text{'}}=2\overrightarrow{OD}$.

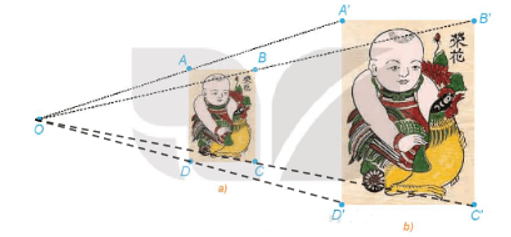
Từ đó ta có các điểm A', B', C', D' lần lượt là ảnh của các điểm A, B, C, D qua phép vị tự V_{(O, 2)}. Do đó, phép vị tự V_{(O, 2)} biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'.

Vậy phép vị tự V_{(O, 2)­} biến bức tranh nhỏ thành bức tranh lớn. Khi đó, phép vị tự $V_{\left(O,\frac{1}{2}\right)}$ biến bức tranh lớn thành bức tranh nhỏ.

2. Tính chất

HĐ2 trang 27 Chuyên đề Toán 11: Cho phép vị tự tâm O, tỉ số k biến điểm M thành điểm M'¸điểm N thành điểm N'.

a) Biểu diễn các vectơ $\overrightarrow{OM\text{'}},\overrightarrow{ON\text{'}}$ tương ứng theo các vectơ $\overrightarrow{OM},\overrightarrow{ON}$.

b) Giải thích vì sao $\overrightarrow{M\text{'}N\text{'}}=k\overrightarrow{MN}$.

Lời giải:

a) Phép vị tự tâm O, tỉ số k biến điểm M thành điểm M', điểm N thành điểm N' nên ta có $\overrightarrow{OM\text{'}}=k\overrightarrow{OM}$ và $\overrightarrow{ON\text{'}}=k\overrightarrow{ON}$.

b) Ta có: $\overrightarrow{M\text{'}N\text{'}}=\overrightarrow{ON\text{'}}-\overrightarrow{OM\text{'}}=k\overrightarrow{ON}-K\overrightarrow{OM}=k\left(\overrightarrow{ON}-\overrightarrow{OM}\right)=k\overrightarrow{MN}$ (theo quy tắc hiệu).

Vậy $\overrightarrow{M\text{'}N\text{'}}=k\overrightarrow{MN}$.

Luyện tập 2 trang 28 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 1)² + (y – 2)² = 25.

a) Tìm tâm I và bán kính R của đường tròn (C).

b) Tìm tâm I' và bán kính R' của đường tròn (C') là ảnh của đường tròn (C) qua phép vị tự tâm A(3; 5), tỉ số 2.

c) Viết phương trình của (C').

Lời giải:

a) Ta có (C): (x – 1)² + (y – 2)² = 25 hay (x – 1)² + (y – 2)² = 5².

Do đó, đường tròn (C) có tâm I(1; 2) và bán kính R = 5.

b) Đường tròn (C') là ảnh của đường tròn (C) qua phép vị tự tâm A(3; 5), tỉ số 2 nên tâm I' của đường tròn (C') là ảnh của tâm I của đường tròn (C) qua phép vị tự V_{(A, 2)} và bán kính R' của đường tròn (C') bằng 2 lần bán kính R của đường tròn (C) hay R' = 2 . 5 = 10.

Ta có: $\overrightarrow{AI}=\left(1-3;2-5\right)=\left(-2;-3\right)$.

Vì I' là ảnh của I qua phép vị tự V_{(A, 2)} nên $\overrightarrow{AI\text{'}}=2\overrightarrow{AI}$

  $\iff \left\{\begin{array}{l}{x}_{I\text{'}}-x_A=2.\left(-2\right)\\ y_{I\text{'}}-y_A=2.\left(-3\right)\end{array}\right.\iff \left\{\begin{array}{l}{x}_{I\text{'}}-3=-4\\ y_{I\text{'}}-5=-6\end{array}\right.\iff \left\{\begin{array}{l}{x}_{I\text{'}}=-1\\ y_{I\text{'}}=-1\end{array}\right.$.

Vậy I'(– 1; – 1) và R' = 10.

c) Phương trình đường tròn (C') là (x + 1)² + (y + 1)² = 10² hay (x + 1)² + (y + 1)² = 100.

Vận dụng 2 trang 29 Chuyên đề Toán 11: Quan sát Hình 1.47 và cho biết hình nào trong hai hình nhỏ không phải là ảnh của hình lớn qua một phép vị tự. Nêu lí do cho sự lựa chọn đó.

Lời giải:

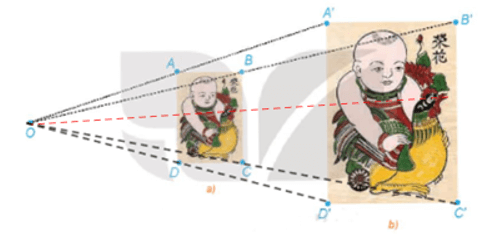
Quan sát Hình 1.47, ta thấy hình b) có hình dạng khác hẳn so với 2 hình còn lại (về cây ở góc trên bên phải, về mây và núi). Mà phép vị tự thì chỉ thay đổi về kích thước mà không thay đổi về hình dạng, do đó hình b) không phải là ảnh của hình lớn qua một phép vị tự.

Bài tập

Bài 1.20 trang 29 Chuyên đề Toán 11: Cho hình thang ABCD có hai đáy AB và CD, CD = 2AB. Gọi O là giao của hai cạnh bên và I là giao của hai đường chéo. Tìm ảnh của đoạn thẳng AB qua các phép vị tự V_{(O, 2)}, V_{(I, – 2)}.

Lời giải:

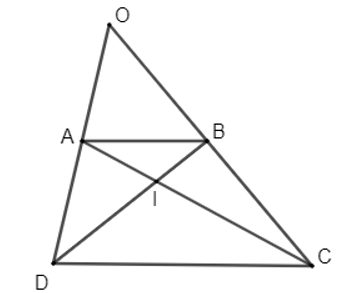
+ Vì ABCD là hình thang có hai đáy AB và CD nên AB // CD. Theo định lí Thales trong tam giác OCD ta có: $\frac{OA}{OD}=\frac{OB}{OC}=\frac{AB}{CD}=\frac{1}{2}$.

Suy ra $\overrightarrow{OD}=2\overrightarrow{OA};\overrightarrow{OC}=2\overrightarrow{OB}$.

Do đó, D và C tương ứng là ảnh của A và B qua phép vị tự V_{(O, 2)}. Vậy đoạn thẳng DC là ảnh của đoạn thẳng AB qua phép vị tự V_{(O, 2)}.

+ Vì AB // CD nên theo hệ quả của định lí Thales trong tam giác ICD ta có:

$\frac{IA}{IC}=\frac{IB}{ID}=\frac{AB}{CD}=\frac{1}{2}$.

Suy ra $\overrightarrow{IC}=-2\overrightarrow{IA};\overrightarrow{ID}=-2\overrightarrow{IB}$.

Do đó, C và D tương ứng là ảnh của A và B qua phép vị tự V_{(I, – 2)}. Vậy đoạn thẳng CD là ảnh của đoạn thẳng AB qua phép vị tự V_{(I, – 2)}.

Bài 1.21 trang 29 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho A(1; 2), B(3; 6). Viết phương trình đường tròn (C) là ảnh của đường tròn đường kính AB qua phép vị tự V_{(O, 3)}.

Lời giải:

Gọi I là trung điểm của AB, ta có I(2; 4) là tâm của đường tròn đường kính AB với bán kính là R = IA = $\sqrt{{\left(1-2\right)}^2+{\left(2-4\right)}^2}=\sqrt{5}$.

Gọi I' và R' lần lượt là tâm và bán kính của đường tròn (C).

Vì đường tròn (C) là ảnh của đường tròn đường kính AB qua phép vị tự V_{(O, 3)} nên I' là ảnh của I qua phép vị tự V_{(O, 3)} và R' = 3R = $3\sqrt{5}$.

Khi đó ta có: $\overrightarrow{OI\text{'}}=3\overrightarrow{OI}$. Từ đó suy ra I'(6; 12).

Phương trình đường tròn (C) là (x – 6)² + (y – 12)² = ${\left(3\sqrt{5}\right)}^2$hay (x – 6)² + (y – 12)² = 45.

Bài 1.22 trang 29 Chuyên đề Toán 11: Ở Hình 1.48, A', B', C', D', E' tương ứng là trung điểm của các đoạn thẳng IA, IB, IC, ID, IE. Hỏi năm điểm đó có thuộc một đường tròn hay không? Vì sao?

Lời giải:

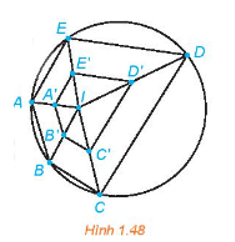
Vì A', B', C', D', E' tương ứng là trung điểm của các đoạn thẳng IA, IB, IC, ID, IE nên ta suy ra $\overrightarrow{IA\text{'}}=\frac{1}{2}\overrightarrow{IA};\overrightarrow{IB\text{'}}=\frac{1}{2}\overrightarrow{IB};\overrightarrow{IC\text{'}}=\frac{1}{2}\overrightarrow{IC};\overrightarrow{ID\text{'}}=\frac{1}{2}\overrightarrow{ID};\overrightarrow{IE\text{'}}=\frac{1}{2}\overrightarrow{IE}$. Do đó, A', B', C', D', E' tương ứng là ảnh của các điểm A, B, C, D, E qua phép vị tự tâm I, tỉ số $\frac{1}{2}$.

Từ Hình 1.48, ta thấy các điểm A, B, C, D, E cùng thuộc một đường tròn. Vậy các điểm A', B', C', D', E' đều cùng thuộc một đường tròn là ảnh của đường tròn đi qua 5 điểm A, B, C, D, E qua phép vị tự tâm I, tỉ số $\frac{1}{2}$.

Bài 1.23 trang 29 Chuyên đề Toán 11: Quan sát ba hình được tô màu ở Hình 1.49, hình nhỏ nào là ảnh của hình lớn qua một phép vị tự?

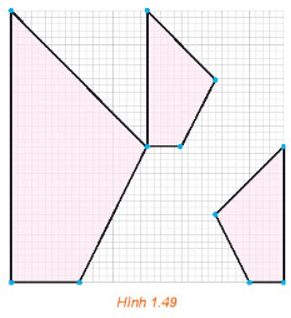
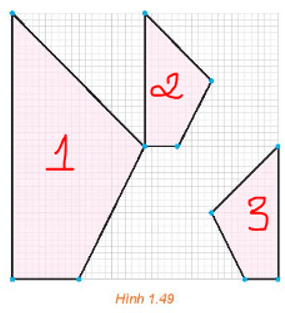
Lời giải:

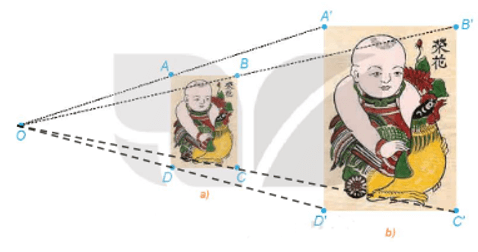
Hình nhỏ 2 là ảnh của hình lớn qua một phép vị tự.

Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 3: Phép đối xứng trục

Bài 4: Phép quay và phép đối xứng tâm

Bài 5: Phép dời hình

Bài 7: Phép đồng dạng

Bài tập cuối chuyên đề 1