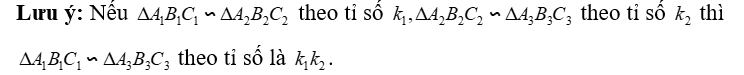Chuyên đề Tam giác đồng dạng lớp 8 | Chuyên đề dạy thêm Toán 8
Tài liệu Chuyên đề Tam giác đồng dạng lớp 8 gồm các dạng bài tập trắc nghiệm và tự luận từ cơ bản đến nâng cao giúp thầy cô có thêm tài liệu giảng dạy Toán lớp 8.
Chỉ từ 500k mua trọn bộ (Chuyên đề) Phương pháp giải Toán 8 (cơ bản, nâng cao) word có lời giải chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Chủ đề 33: HAI TAM GIÁC ĐỒNG DẠNG
A. PHƯƠNG PHÁP
1. Định nghĩa
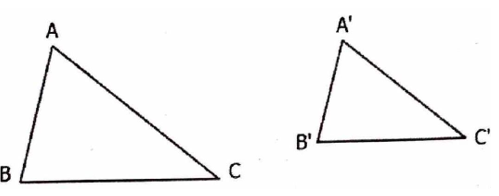
Hai tam giác gọi là đồng dạng với nhau nếu chúng có 3 cặp góc bằng nhau đôi một và 3 cặp cạnh tương ứng tỉ lệ.
và có:
Khi đó:
Khi hai tam giác đồng dạng với nhau, ta có:
+ Các góc bằng nhau gọi là các góc tương ứng.
+ Các đỉnh của các góc bằng nhau gọi là các đỉnh tương ứng.
+ Các cạnh đối diện với góc bằng nhau gọi là các cạnh tương ứng.
+ Khi dùng ký hiệu thì phải ghi đúng thứ tự cặp đỉnh tương ứng.
+ Tỉ số của hai cạnh tương ứng k gọi là tỉ số đồng dạng.
2. Tính chất
a. Phản xạ:
b. Đối xứng: theo tỉ số
c. Bắc cầu :
Suy ra: .
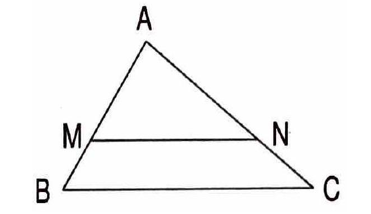
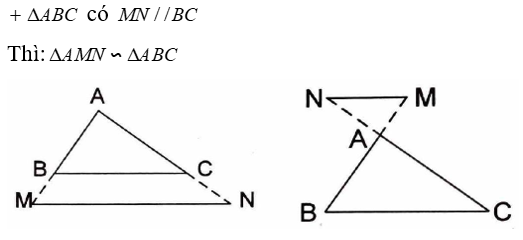
3. Định lí: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác đồng dạng với tam giác đã cho.
Như vậy:
có
Thì:
Lưu ý. Định lí trên cũng đúng trong trường hợp đường thẳng a cắt phần kéo dài hai cạnh của tam giác và song song với cạnh còn lại.
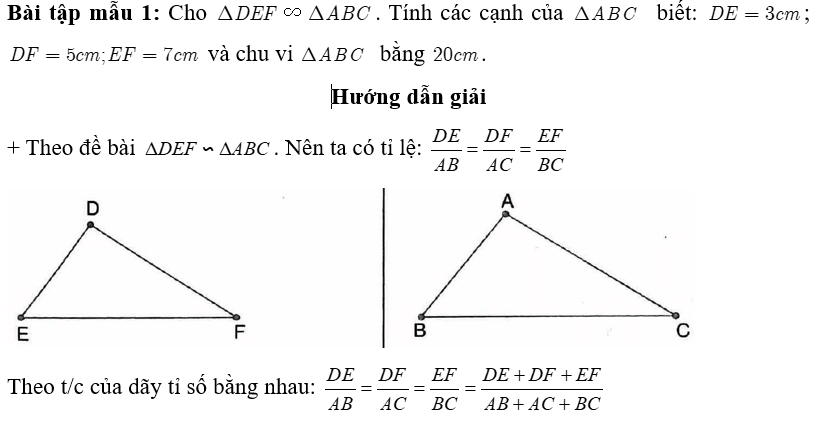
B. BÀI TẬP MẪU
Hay
Suy ra: .
Bài tập mẫu 3: Tam giác có chu vi là 30cm và độ dài các cạnh lần lượt là và . Tìm độ dài các cạnh của một . Biết
Hướng dẫn giải
Theo đề bài: Nên:
Ta cần tìm tỉ lệ này để tính độ dài các cạnh của tam giác .
Ta có: hay
Đặt . Khi đó:
Do đó: :
Thay vào: Từ đây ta tính được:
Do đó, độ dài các cạnh của là:
Vậy: có độ dài các cạnh lần lượt là và .
Bài tập mẫu 4: Cho . Biết và . Tính độ dài cạnh của .
Hướng dẫn giải
Theo đề bài ta có nên:
Thay vào: hay \(DE = \frac{{6 \times 10}}{8} = 7,5\left( {{\rm{\;cm}}} \right)
Vậy độ dài cạnh của là .
Bài tập mẫu 5: Trong hình vuông ABCD, M là trung điểm của cạnh CD và N là trung điểm của cạnh AD. Kẻ đường thẳng qua M và N cắt đường chéo BD tại H. Tính độ dài BH biết rằng
Hướng dẫn giải
Gọi là độ dài cạnh của hình vuông .
Do là trung điểm của , ta có .
Tương tự, do là trung điểm của , ta có .
................................
................................
................................
Xem thử tài liệu tại đây: Link tài liệu
Chuyên đề Phương trình bậc nhất và hàm số bậc nhất
Xem thêm các chương trình khác:
- Soạn văn 8 Kết nối tri thức (hay nhất)
- Văn mẫu lớp 8 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 8 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn lớp 8 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 8 - Kết nối tri thức
- Giải SBT Ngữ văn 8 – Kết nối tri thức
- Giải Vở thực hành Ngữ văn 8 Kết nối tri thức | VTH Ngữ văn 8 Tập 1, Tập 2
- Nội dung chính tác phẩm Ngữ văn lớp 8 – Kết nối tri thức
- Soạn văn 8 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 8 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 8 – Global success
- Giải sbt Tiếng Anh 8 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 8 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 8 Global success
- Giải sgk Khoa học tự nhiên 8 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 8 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 8 – Kết nối tri thức
- Giải vth Khoa học tự nhiên 8 – Kết nối tri thức
- Giải sgk Lịch sử 8 – Kết nối tri thức
- Lý thuyết Lịch sử 8 - Kết nối tri thức
- Giải sbt Lịch sử 8 – Kết nối tri thức
- Giải sgk Địa lí 8 – Kết nối tri thức
- Lý thuyết Địa lí 8 - Kết nối tri thức
- Giải sbt Địa lí 8 – Kết nối tri thức
- Giải VTH Địa lí 8 Kết nối tri thức | Vở thực hành Địa lí 8
- Giải sgk Giáo dục công dân 8 – Kết nối tri thức
- Lý thuyết Giáo dục công dân 8 – Kết nối tri thức
- Giải sbt Giáo dục công dân 8 – Kết nối tri thức
- Giải sgk Công nghệ 8 – Kết nối tri thức
- Lý thuyết Công nghệ 8 - Kết nối tri thức
- Giải sbt Công nghệ 8 – Kết nối tri thức
- Giải sgk Tin học 8 – Kết nối tri thức
- Lý thuyết Tin học 8 - Kết nối tri thức
- Giải sbt Tin học 8 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 8 – Kết nối tri thức