Chuyên đề Tứ giác lớp 8 | Chuyên đề dạy thêm Toán 8

Chỉ từ 500k mua trọn bộ (Chuyên đề) Phương pháp giải Toán 8 (cơ bản, nâng cao) word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Chủ đề 10: TỨ GIÁC

Dạng 1: TÍNH SỐ ĐO GÓC

A. PHƯƠNG PHÁP

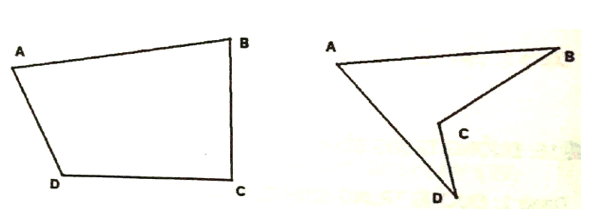
1. Định nghĩa: Tứ giác $ABCD$ là hình gồm 4 đoạn thẳng $AB,BC,CD,DA$. Trong đó bất kỳ hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Tứ giác lồi là tứ giác luôn nằm trong một nưa mặt phẳng mà bò là đường thẳng chứa bất kì cạnh nào của tứ giác.

Từ nay, khi nói đến tứ giác mà không chú thích gì thêm ta hiểu đó là tứ giác lồi.

2. Tính chất:

+ Tổng bốn góc của một tứ giác bằng ${360}^{\circ }$.

+ Tổng các góc ngoài của một tứ giác lồi bằng ${360}^{\circ }$.

+ Bạn đọc cũng cần sử dụng các mối quan hệ về góc đối đỉnh, góc so le trong, góc kề bù, tổng ba góc của một tam giác...

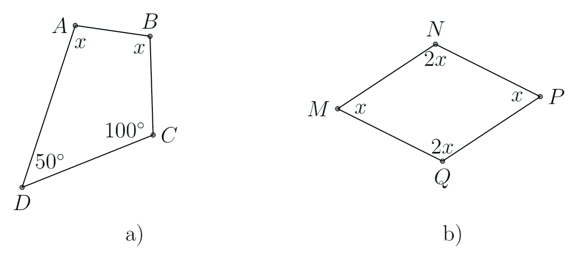
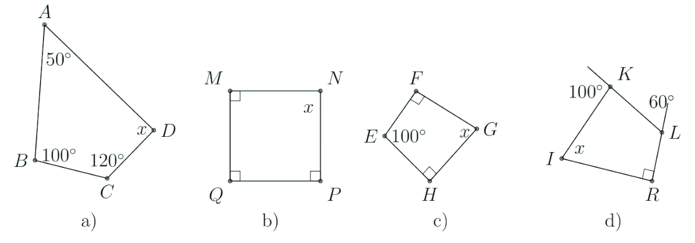
Bài tập mẫu 1: Tìm x trong các hình vẽ sau

Hướng dẫn giải

a. Tổng các góc trong tứ giác là ${360}^{\circ }$

Nên $\hat{A}+\hat{B}+\hat{C}+\hat{D}={360}^{\circ }$

Suy ra: $x+x+{50}^{\circ }+{110}^{\circ }={360}^{\circ }$

Do đó: $x={100}^{\circ }$

b. Tổng các góc trong tứ giác là ${360}^{\circ }$

Nên $\hat{M}+\hat{N}+\hat{P}+\hat{Q}={360}^{\circ }$.

Do đó: $x+2x+x+2x={360}^{\circ }$

Suy ra: $6x={360}^{\circ }$ hay $x={60}^{\circ }$

Bài tập mẫu 2: Tứ giác $MNPQ$ có $\hat{M}={65}^{\circ };\hat{N}={117}^{\circ };\hat{P}={71}^{\circ }$. Tính số đo góc ngoài tại đỉnh Q.

Hướng dẫn giải

Tổng các góc trong tứ giác $MNPQ$ là ${360}^{\circ }$

Nên $\hat{M}+\hat{N}+\hat{P}+\hat{Q}={360}^{\circ }$.

Thay số vào ta tính được: $\hat{Q}={107}^{\circ }$.

Nên góc ngoài tại đỉnh $Q$ là: ${180}^{\circ }-{107}^{\circ }={73}^{\circ }$

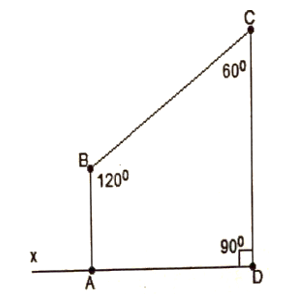
Bài tập mẫu 3: Cho tứ giác $ABCD$ có $\hat{B}={120}^{\circ },\hat{C}={60}^{\circ },\hat{D}={90}^{\circ }$. Tính góc $\hat{A}$ và góc ngoài của tứ giác tại đỉnh A.

Hướng dẫn giải

Tổng các góc trong tứ giác $ABCD$ ta có: $\hat{A}+\hat{B}+\hat{C}+\hat{D}={360}^{\circ }$

$\hat{A}={360}^{\circ }-(\hat{B}+\hat{C}+\hat{D})$

$\hat{A}={360}^{\circ }-\left({120}^{\circ }+{60}^{\circ }+{90}^{\circ }\right)={90}^{\circ }$

$\widehat{xAB}$ là một góc ngoài của $\hat{A}$

$\widehat{xAB}+\hat{A}={180}^{\circ };\widehat{xAB}={180}^{\circ }-\hat{A}={180}^{\circ }-{90}^{\circ }={90}^{\circ }$

$\widehat{xAB}={180}^{\circ }-\hat{A}={180}^{\circ }-{90}^{\circ }={90}^{\circ }$

Bài tập mẫu 4:

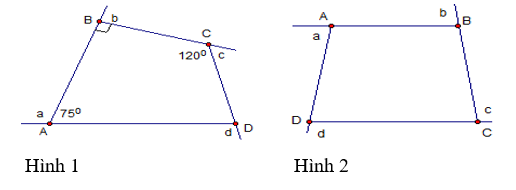
a. Tính các góc ngoài của tứ giác ở hình 1.

b. Tính tổng các góc ngoài của một tứ giác ở hình 2 (Tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài)

Hướng dẫn giải

a. Tổng các góc trong tứ giác $\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$.

Thay vào ta được: $a+\hat{A}={180}^{\circ }$. Do đó: $a={180}^{\circ }-\hat{A}={180}^{\circ }-{75}^{\circ }={105}^{\circ }$

Mặt khác: $b+\hat{B}={180}^{\circ }$. Nên: $b={180}^{\circ }-\hat{B}={180}^{\circ }-{90}^{\circ }={90}^{\circ }$

Tương tự: $c+\hat{C}={180}^{\circ }$. Hay $c={180}^{\circ }-\hat{C}={180}^{\circ }-{120}^{\circ }={60}^{\circ }$

Và: $d+\hat{D}={180}^{\circ }$. Suy ra: $d={180}^{\circ }-\hat{D}={180}^{\circ }-{75}^{\circ }={105}^{\circ }$

b. Trong tứ giác $\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}:\hat{A}+\hat{B}+\hat{C}+\hat{D}={360}^{\circ }$

$a+b+c+d=\left({180}^{\circ }-\hat{A}\right)+\left({180}^{\circ }-\hat{B}\right)+\left({180}^{\circ }-\hat{C}\right)+\left({180}^{\circ }-\hat{D}\right)$

$={720}^{\circ }-\left(\hat{A}+\hat{B}+\hat{C}+\hat{D}\right)={720}^{\circ }-{360}^{\circ }={360}^{\circ }$

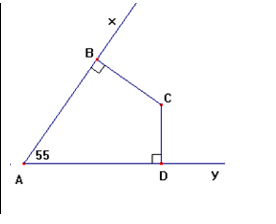
Bài tập mẫu 5:Cho hình vẽ bên ; Tính $\widehat{BCD}$

Hướng dẫn giải

Dễ thấy: $\widehat{BCD}={360}^{\circ }-{90}^{\circ }-{90}^{\circ }-{55}^{\circ }={125}^{\circ }$

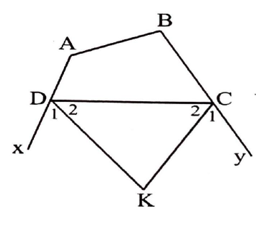
Bài tập mẫu 6: Cho tứ giác $ABCD$ có $\hat{A}+\hat{B}={220}^{\circ }.$ Các tia phân giác ngoài tại đỉnh C và D cắt nhau tại K. Tính số đo của góc$\widehat{CKD}$.

Hướng dẫn giải

Ta có $\widehat{CDx}+\widehat{DCy}=\hat{A}+\hat{B}={220}^{\circ }$

Suy ra $:\frac{\widehat{CDx}+\widehat{CDy}}{2}={110}^{\circ }$

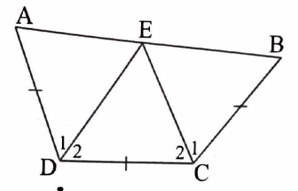
Bài tập mẫu 7: Cho tứ giác $ABCD$ có$AD=DC=CB$; $\hat{C}={130}^{\circ };$ $\hat{D}={110}^{\circ }.$ Tính số đo$\hat{A},\hat{B}$.

Hướng dẫn giải

Vẽ đường phân giác của các góc $\hat{C}$ và $\hat{D}$ chúng cắt nhau tại $\mathrm{E}$.

Xét $\mathrm{\Delta }\mathrm{E}\mathrm{C}\mathrm{D}$ có: $\widehat{CED}={180}^{\circ }-\frac{{110}^{\circ }+{130}^{\circ }}{2}={60}^{\circ }$.

Nên: $\mathrm{\Delta }ADE=\mathrm{\Delta }CDE($ c.g.c $)$. Do đó: $\widehat{AED}=\widehat{CED}={60}^{\circ }$.

Mặt khác: $\mathrm{\Delta }BCE=\mathrm{\Delta }DCE($ c.g.c $)$

Nên: $\widehat{BEC}=\widehat{DEC}={60}^{\circ }$.

Suy ra: $\widehat{AEB}={180}^{\circ }$

Do đó: $A;E;B$ thẳng hàng.

Vậy $\widehat{BAD}=\widehat{EAD}=\widehat{ECD}={65}^{\circ }$.

Do đó $\widehat{ABC}={360}^{\circ }-\left({65}^{\circ }+{110}^{\circ }+{130}^{\circ }\right)={55}^{\circ }$.

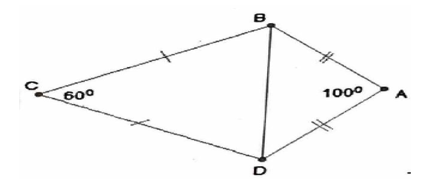
Bài tập mẫu 8: Cho tứ giác $ABCD$ có $AB=AD,CB=CD,\hat{C}={60}^{\circ },\hat{A}={100}^{\circ }$.

a. Chứng minh AC là đường trung trực của BD.

b. Tính $\hat{B},\hat{D}$?

Hướng dẫn giải

a. Ta có: $AB=AD\left(gt\right)$.

Nên: A thuộc đường trung trực của $\mathrm{B}\mathrm{D}$ :

Mặt khác: $CB=CD\left(\mathrm{g}\mathrm{t}\right)$

Do đó: $\mathrm{C}$ thuộc đường trung trực của $\mathrm{B}\mathrm{D}$

Vậy $\mathrm{A}\mathrm{C}$ là đường trung trực của $\mathrm{B}\mathrm{D}$.

b. Ta có: $\mathrm{\Delta }ABD$ cân tại $\mathrm{A}\left(AB=AD\right)$ nên $\widehat{ABD}=\widehat{ADB}$

Mà $\mathrm{\Delta }CBD$ cân tại $C\left(CB=CD\right)$. Nên $\widehat{CBD}=\widehat{CDB}$

Do đó: $\{\begin{array}{l}\hat{B}=\widehat{CBA}=\widehat{CBD}+\widehat{DBA}\\ \hat{D}=\widehat{DA}=\widehat{CDB}+\widehat{BDA}\end{array}$

Suy ra: $\hat{B}=\hat{D}$

C. BÀI TẬP LUYỆN TẬP

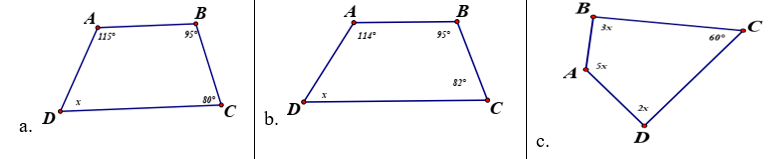
Bài tập 1: Cho tứ giác $ABCD$ như hình vẽ bên dưới. Tìm x trong các hình vẽ

Bài tập 2: Cho tứ giác $ABCD$ như hình vẽ bên dưới. Tìm x trong các hình vẽ

Bài tập 3: Cho tứ giác $ABCD$ biết $\hat{A}={75}^{\circ };\hat{B}={90}^{\circ };\hat{C}={120}^{\circ }$. Tính số đo các góc ngoài của tứ giác $ABCD$ .

Bài tập 4. Cho tứ giác $ABCD$ có $AB=BC;CD=DA$.

1. Chứng minh $BD$ là đường trung trực của $AC$

2. Cho $\hat{B}={100}^{\circ },\hat{D}={80}^{\circ }$. Tính $\hat{A}$ và $\hat{C}$.

Bài tập 5. Cho tứ giác $ABCD$ biết rằng $\frac{\hat{A}}{1}=\frac{\hat{B}}{2}=\frac{\hat{C}}{3}=\frac{\hat{D}}{4}$. Tính các góc của tứ giác $ABCD$.

Bài tập 6. Cho tứ giác $MNPQ$ có $\hat{N}=\hat{M}+{10}^{\circ },\hat{P}=\hat{N}+{10}^{\circ },\hat{Q}=\hat{P}+{10}^{\circ }$. Hãy tính các góc của tứ giác $MNPQ$.

Bài tập 7. Tứ giác $ABCD$ có $\hat{C}={60}^{\circ },\hat{D}={80}^{\circ },\hat{A}-\hat{B}={10}^{\circ }$. Tính số đo của$\hat{A}$ và $\hat{B}$

D. HƯỚNG DẪN GIẢI HOẶC ĐÁP SỐ

Bài tập 1:

a. $x=70$

b. $x={69}^{\circ }$

c.$x={30}^{\circ }$
Bài tập 2:

a. ${90}^{\circ }$

b. ${90}^{\circ }$

c. ${80}^{\circ }$

d. ${70}^{\circ }$

Bài tập 3:

Góc ngoài tại đỉnh $\mathrm{A}$ có số đo là: ${105}^{\circ }$

Góc ngoài tại đỉnh B có số đo là: ${90}^{\circ }$

Góc ngoài tại đỉnh $C$ có số đo là: ${60}^{\circ }$

Góc ngoài tại đỉnh $\mathrm{D}$ có số đo là: ${105}^{\circ }$

................................

................................

................................

Xem thử tài liệu tại đây: Link tài liệu

• Xem thêm các chuyên đề dạy thêm Toán 8 hay, chi tiết khác:

Chuyên đề Định lí Thalès

Chuyên đề Dữ liệu và biểu đồ

Chuyên đề Phân thức đại số

Chuyên đề Phương trình bậc nhất và hàm số bậc nhất

Chuyên đề Mở đầu về tính xác suất của biến cố