Câu hỏi:
05/11/2024 5,132
Với a là số thực dương tùy ý, log3(9a) bằng
A. 2log3a.
B. 9+log3a.
C. 2+log3a.
D. 2−log3a.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
Ta có log3(9a)=log39+log3a=log332+log3a=2+log3a.
Đáp án đúng là C.
*Phương pháp giải:
a. Đưa về cùng cơ số
- Áp dụng một số tính chất của lôgarit:
loga(x.y)=logax+logaylogaxy=logax−logaylogabα=α.logablogab=logcblogcalogaαb=1αlogab (α≠0)
b. Đặt ẩn phụ
c. Mũ hóa.
*LÝ thuyết :
- Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
- Phương trình lôgarit cơ bản có dạng: logax=b (a>0,a≠1)
Theo định nghĩa lôgarit ta có: logax=b⇔x=ab
Xem thêm
Phương trình lôgarit | Lý thuyết, công thức, các dạng bài tập và cách giải
TOP 40 câu Trắc nghiệm Logarit (có đáp án 2024) - Toán 12
Lời giải:
Ta có log3(9a)=log39+log3a=log332+log3a=2+log3a.
Đáp án đúng là C.
*Phương pháp giải:
a. Đưa về cùng cơ số
- Áp dụng một số tính chất của lôgarit:
loga(x.y)=logax+logaylogaxy=logax−logaylogabα=α.logablogab=logcblogcalogaαb=1αlogab (α≠0)
b. Đặt ẩn phụ
c. Mũ hóa.
*LÝ thuyết :
- Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
- Phương trình lôgarit cơ bản có dạng: logax=b (a>0,a≠1)
Theo định nghĩa lôgarit ta có: logax=b⇔x=ab
Xem thêm
Phương trình lôgarit | Lý thuyết, công thức, các dạng bài tập và cách giải
TOP 40 câu Trắc nghiệm Logarit (có đáp án 2024) - Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Các mặt của một con súc sắc được đánh số từ 1 đến 6. Người ta gieo con súc sắc 3 lần liên tiếp và nhân các con số nhận được trong mỗi lần gieo với nhau. Tính xác suất để tích thu được là một số chia hết cho 6.
Các mặt của một con súc sắc được đánh số từ 1 đến 6. Người ta gieo con súc sắc 3 lần liên tiếp và nhân các con số nhận được trong mỗi lần gieo với nhau. Tính xác suất để tích thu được là một số chia hết cho 6.
Câu 2:
Giả sử 9∫0f(x)dx=37 và 0∫9g(x)dx=16. Khi đó, I=9∫0[2f(x)+3g(x)]dx bằng
Câu 3:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x3+3x2−x và đồ thị hàm số y=2x2+x.
Câu 4:
Cho hàm số y=f(2−x) có bảng xét dấu đạo hàm như sau:

Hàm số h(x)=f(x2−2) có bao nhiêu điểm cực trị?
Câu 5:
Đồ thị hàm số y=2x−3x−1 có các đường tiệm cận đứng và tiệm cận ngang lần lượt là
Câu 6:
Cho hàm số y = f(x) liên tục trên ℝ và thỏa mãn f3(x)+f(x)=x với mọi x∈ℝ. Tính I=2∫0f(x)dx.
Cho hàm số y = f(x) liên tục trên ℝ và thỏa mãn f3(x)+f(x)=x với mọi x∈ℝ. Tính I=2∫0f(x)dx.
Câu 7:
Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều cạnh AB = 2a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của AB. Biết góc giữa cạnh bên và mặt đáy bằng 600. Tính theo a khoảng cách H từ điểm B đến mặt phẳng (ACC'A').
Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều cạnh AB = 2a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của AB. Biết góc giữa cạnh bên và mặt đáy bằng 600. Tính theo a khoảng cách H từ điểm B đến mặt phẳng (ACC'A').
Câu 8:
Đường thẳng y = 4x - 1 và đồ thị hàm số y=x3−3x2−1 có bao nhiêu điểm chung?
Đường thẳng y = 4x - 1 và đồ thị hàm số y=x3−3x2−1 có bao nhiêu điểm chung?
Câu 9:
Một hộp có 3 viên bi đỏ và 4 viên bi xanh. Số cách lấy ra hai viên bi, trong đó có 1 viên bi đỏ và 1 viên bi xanh bằng
Câu 10:
Có bao nhiêu giá trị nguyên của tham số m∈(−2020;2021) sao cho hàm số y=3x+18x−m nghịch biến trên khoảng (−∞;−3)?
Có bao nhiêu giá trị nguyên của tham số m∈(−2020;2021) sao cho hàm số y=3x+18x−m nghịch biến trên khoảng (−∞;−3)?
Câu 12:
Cho hình lập phương có thể tích bằng 64a3. Thể tích của khối cầu nội tiếp hình lập phương đó bằng
Câu 13:
Cho hình lập phương có thể tích bằng 64a3. Thể tích của khối cầu nội tiếp hình lập phương đó bằng
Câu 14:
Trong không gian Oxyz cho điểm A(1;-2;3). Hình chiếu vuông góc của điểm A trên mặt phẳng (Oyz) là điểm M. Tọa độ của điểm M là
Trong không gian Oxyz cho điểm A(1;-2;3). Hình chiếu vuông góc của điểm A trên mặt phẳng (Oyz) là điểm M. Tọa độ của điểm M là
Câu 15:
Cho hàm số f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên dưới.
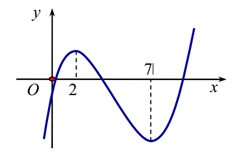
Khẳng định nào sau đây là đúng?
Cho hàm số f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên dưới.

Khẳng định nào sau đây là đúng?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)