Câu hỏi:
19/11/2024 339Trong các hàm số sau, hàm số nào nghịch biến trên (-∞;+∞) ?
A. y=−x4+3x2−2x+1
B. y=x+12x−2
C. y=−x3+x2−2x+1
D. y=x3+3.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: C
* Lời giải:
Loại A và B vì hàm bậc bốn và hàm bậc nhất trên bậc nhất không bao giờ đơn điệu trên (−∞;+∞) .
Xét hàm y=−x3+x2−2x+1
TXĐ: D =
Ta có: y'
Suy ra hàm số nghịch biến trên .
Xét hàm: .
TXĐ: .
Ta có: ; suy ra hàm số đồng biến trên .
* Phương pháp giải:
- Tìm điều kiện cho hàm số đó xác định rồi tính đạo hàm và xét sự đồng biến/nghịch biến của hàm số đó trên bảng biến thiên
* Một số lý thuyết liên quan và dạng bài toán về đồng biến/nghịch biến:
a) Dạng 1: Tìm các khoảng đơn điệu của hàm số.
* Phương pháp làm bài:
– Bước 1: Tìm tập xác định của hàm số đã cho.
– Bước 2: Tính đạo hàm f′(x) , sau đó tìm các điểm x1,x2,…,xn mà tại đó đạo hàm của hàm số bằng 0 hoặc không xác định.
– Bước 3: Xét dấu đạo hàm và đưa ra kết luận về khoảng đồng biến và nghịch biến của hàm số.
+ Các khoảng mà f′(x)>0 là các khoảng đồng biến của hàm số.
+ Các khoảng mà f′(x)<0 là các khoảng nghịch biến của hàm số.
b) Dạng 2: Tìm giá trị của m để hàm số đơn điệu trên R.
* Phương pháp làm bài:
– Bước 1: Tính f′(x).
– Bước 2: Nêu các điều kiện của bài toán:
+ Hàm số y=f(x) đồng biến trên R⇔y′=f′(x)⩾0,với ∀x∈R và y′=0 tại một hữu hạn điểm.
+ Hàm số y=f(x) nghịch biến trên R⇔y′=f′(x)⩽0,với ∀x∈R và y′=0 tại một hữu hạn điểm.
– Bước 3: Từ các điều kiện trên sử dụng các kiến thức về dấu của nhị thức bậc nhất và tam thức bậc hai để tìm m.
c) Dạng 3: Tìm m để hàm số đơn điệu trên miền D đã cho trước.
* Phương pháp làm bài:
– Bước 1: Nêu các điều kiện để hàm số đơn điệu trên D:
+ Hàm số y=f(x) đồng biến trên D⇔y′=f′(x)⩾0, với ∀x∈D.
+ Hàm số y=f(x) nghịch biến trên D⇔y′=f′(x)⩽0,với ∀x∈D.
– Bước 2: Từ điều kiện trên hãy sử dụng các cách suy luận khác nhau cho từng bài toán để tìm m.
- Bước 3: Kết luận
d) Dạng 4: Tìm m để hàm số đồng biến, nghịch biến trên khoảng
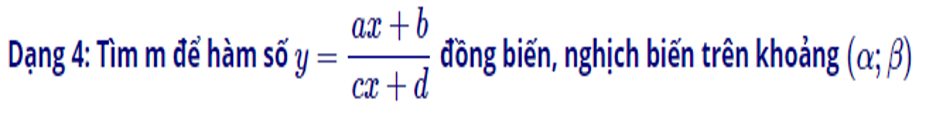
– Bước 1: Tính y′
– Bước 2: Nêu điều kiện để hàm số đồng biến và nghịch biến:
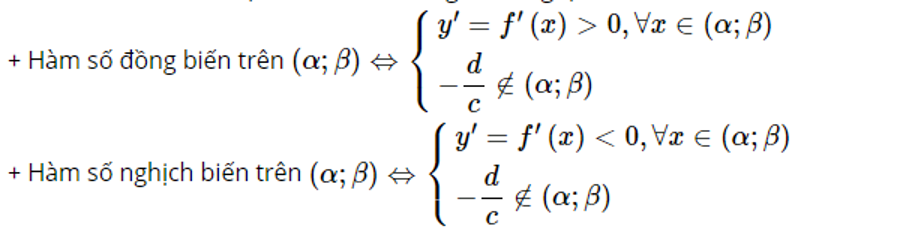
– Bước 3: Đưa ra kết luận.
Xem thêm các bài viết liên quan hay, chi tiết:
50 bài tập về sự đồng biến và nghịch biến của hàm số (có đáp án 2024) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Trong trò chơi “Chiếc nón kì diệu” chiếc kim của bánh xe có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Tính xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau.
Câu 5:
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng nào trong các mặt phẳng sau song song với trục Oz?
Câu 6:
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số và các đường được xác định bởi công thức:
Câu 7:
Trong không gian với hệ tọa độ Oxyz, lập phương trình của các mặt phẳng song song với mặt phẳng và cách một khoảng bằng .
Câu 8:
Cho hình nón tròn xoay có đường cao h = 20cm . Gọi là góc ở đỉnh của hình nón với . Độ dài đường sinh của hình nón là
Câu 9:
Công thức nào sau đây là đúng với một cấp số cộng có số hạng đầu , công sai d và số tự nhiên .
Câu 10:
Cho khối lăng trụ tam giác ABC.A’B’C’. Gọi I, J, K lần lượt là trung điểm của các cạnh AB, AA’ và B’C’. Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó.
Câu 11:
Cho hàm số có đạo hàm liên tục trên đoạn [0;1] và thỏa mãn . Biết và . Tích phân bằng.
Câu 12:
Cho hàm số y = f(x) có đồ thị như hình vẽ:
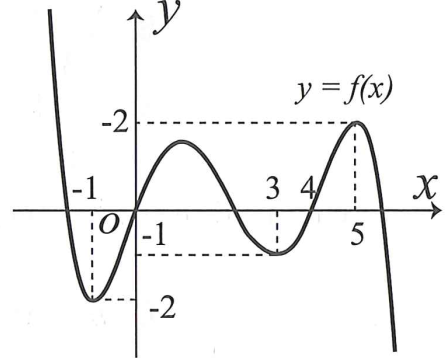
Có bao nhiêu giá trị nguyên của để có nghiệm?
Câu 13:
Có bao nhiêu giá trị m để đồ thị hàm số có đúng hai đường tiệm cận?
Câu 14:
Trong không gian với hệ trục tọa độ Oxyz, nếu là véctơ chỉ phương của trục Oy thì



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)