Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số (x;y) thỏa mãn ${\log }_{x^2+y^2+2}\left(4x+4y-6+m^2\right)\ge 1$ và $x^2+y^2+2x-4y+1=0$.

Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Tính góc giữa hai đường thẳng AB và CD

Gọi n là số nguyên dương sao $\frac{1}{{\log }_{3}x}+\frac{1}{{\log }_{3^2}x}+\frac{1}{{\log }_{3^3}x}+\mathrm{...}+\frac{1}{{\log }_{3^n}x}=\frac{190}{{\log }_{3}x}$ cho đúng với mọi x dương, $x\ne 1$. Tìm giá trị của biểu thức $P=2n+3$.

Cho $\int 2x\left(3x-2\right)dx=A{\left(3x-2\right)}^8+B{\left(3x-2\right)}^7+C$ với $A,B,C\in ℝ$. Tính giá trị của biểu thức $12A+7B$.

Trong không gian với hệ tọa độ Oxyz, cho A(-1;0;0); B(0;0;2); C(0;-3;0). Bán kính mặt cầu ngoại tiếp tứ diện OABC là:

Trong không gian Oxyz, lấy điểm C trên tia Oz sao cho OC = 1. Trên hai tia Ox, Oy lần lượt lấy hai điểm A, B thay đổi sao cho OA + OB = OC. Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện O.ABC?

Cho hàm số có bảng biến thiên như sau:

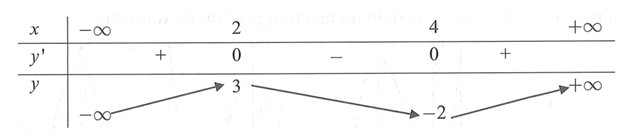
Hàm số đạt cực tiểu tại điểm nào trong các điểm sau đây?

Cho hình chóp S.ABC có đáy là tam giác cân tại $A,AB=AC=a,\widehat{BAC}=120°$. Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC.

Giá trị lớn nhất của hàm số $f\left(x\right)=\frac{x}{x+3}$ trên đoạn [-2;3] bằng:

Tìm số đường tiệm cận của đồ thị hàm số $y=\frac{x-1}{4\sqrt{3x+1}-3x-5}$.

Cho hình chóp S.ABC có các cạnh $SA=BC=3;SB=AC=4;SC=AB=2\sqrt{5}$. Tính thể tích khối chóp S.ABC

Cho hàm số y = f(x) liên tục trên đoạn [0;4] và thỏa mãn điều kiện $4xf\left(x^2\right)+6f\left(2x\right)=\sqrt{4-x^2}$. Tính tích phân $\underset{0}{\overset{4}{\int }}f\left(x\right)dx$.

Cho phương trình: $e^{3m}+e^m=2\left(x+\sqrt{1-x^2}\right)\left(1+x\sqrt{1-x^2}\right)$. Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm.

Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng V. Tính thể tích khối đa diện ABCB’C’.

Cho hàm số y = f(x) có đạo hàm cấp hai trên R. Biết $f\text{'}\left(0\right)=\mathrm{3,}f\text{'}\left(2\right)=-2018$ và bảng xét dấu của f''(x) như sau:

Hàm số $y=f\left(x+2017\right)+2018x$ đạt giá trị nhỏ nhất tại điểm $x_0$ thuộc khoảng nào sau đây?

Tập nghiệm của bất phương trình ${\left(\frac{1}{1+a^2}\right)}^{2x+1}>1$ (với a là tham số, $a\ne 0$) là: