Câu hỏi:
22/07/2024 310
Phương trình x2 – (m – 1)x + m2 – 3m + 2 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
Phương trình x2 – (m – 1)x + m2 – 3m + 2 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
A. m < 3;
A. m < 3;
B. m < 1;
B. m < 1;
C. m = 1;
C. m = 1;
D. 1 < m < 2.
D. 1 < m < 2.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
x2 – (m – 1)x + m2 – 3m + 2 = 0 có 2 nghiệm trái dấu khi a.c < 0
⇔ 1. (m2 – 3m + 2) < 0
⇔ m2 – 3m + 2 < 0
⇔ 1 < m < 2
Vậy phương trình có 2 nghiệm trái dấu khi 1 < m < 2.
Đáp án đúng là D.
Đáp án đúng là: D
x2 – (m – 1)x + m2 – 3m + 2 = 0 có 2 nghiệm trái dấu khi a.c < 0
⇔ 1. (m2 – 3m + 2) < 0
⇔ m2 – 3m + 2 < 0
⇔ 1 < m < 2
Vậy phương trình có 2 nghiệm trái dấu khi 1 < m < 2.
Đáp án đúng là D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :
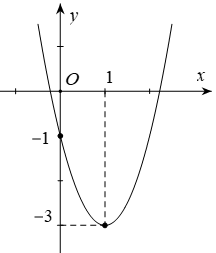
Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :

Câu 2:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
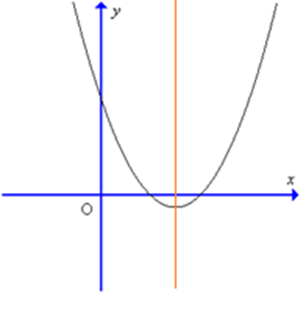
Kết luận nào sau đây đúng về hệ số a, b:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:

Kết luận nào sau đây đúng về hệ số a, b:
Câu 4:
Tổng các nghiệm của phương trình \[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7\] là:
Tổng các nghiệm của phương trình \[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7\] là:
Câu 6:
Tập xác định của hàm số \[y = \frac{{x - 1}}{{{x^2} - x + 3}}\] là
Tập xác định của hàm số \[y = \frac{{x - 1}}{{{x^2} - x + 3}}\] là
Câu 8:
Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
Câu 11:
Cho parabol (P): y = ax2 + bx + 1. Xác định (P) biết rằng parabol đi qua hai điểm A(1; 4) và B(– 1; 2).
Cho parabol (P): y = ax2 + bx + 1. Xác định (P) biết rằng parabol đi qua hai điểm A(1; 4) và B(– 1; 2).
Câu 14:
Tìm tất cả các giá trị của a để bất phương trình ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\)
Tìm tất cả các giá trị của a để bất phương trình ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\)
Câu 15:
Cho bất phương trình 2x2 – 4x + m + 5 > 0. Tìm m để bất phương trình đúng \(\forall x \ge 3\)?
Cho bất phương trình 2x2 – 4x + m + 5 > 0. Tìm m để bất phương trình đúng \(\forall x \ge 3\)?



