Câu hỏi:
13/07/2024 218
Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:
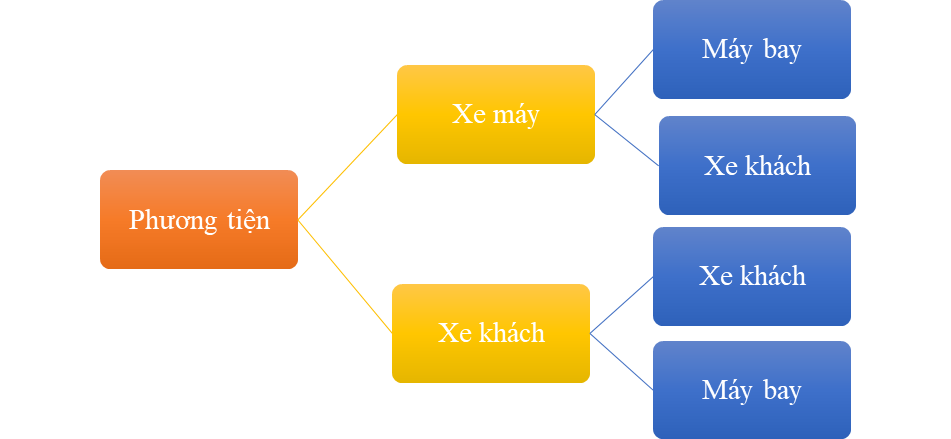
Hỏi bạn Khoa có mấy cách chọn phương tiện đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt?
Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:

Hỏi bạn Khoa có mấy cách chọn phương tiện đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt?
A. 3;
A. 3;
B. 4;
B. 4;
C. 5;
C. 5;
D. 6.
D. 6.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là
Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3; – 1) và B(– 6; 2). Phương trình nào sau đây không phải là phương trình tham số của đường thẳng AB?
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3; – 1) và B(– 6; 2). Phương trình nào sau đây không phải là phương trình tham số của đường thẳng AB?
Câu 3:
Cho n là số tự nhiên. Hãy tính tổng sau:
S = \(C_{2n + 1}^0 + C_{2n + 1}^1 + C_{2n + 1}^2 + ... + C_{2n + 1}^n\).
Cho n là số tự nhiên. Hãy tính tổng sau:
S = \(C_{2n + 1}^0 + C_{2n + 1}^1 + C_{2n + 1}^2 + ... + C_{2n + 1}^n\).
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho hai vectơ \(\overrightarrow a = \left( {4;\,\, - m} \right)\) và \(\overrightarrow b = \left( {2m + 6;\,\,1} \right)\). Tập giá trị của m để hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương là
Trong mặt phẳng tọa độ Oxy, cho hai vectơ \(\overrightarrow a = \left( {4;\,\, - m} \right)\) và \(\overrightarrow b = \left( {2m + 6;\,\,1} \right)\). Tập giá trị của m để hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương là
Câu 5:
Với n là số nguyên dương tùy ý lớn hơn 1, mệnh đề nào dưới đây đúng?
Với n là số nguyên dương tùy ý lớn hơn 1, mệnh đề nào dưới đây đúng?
Câu 6:
Cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 8 - \left( {m + 1} \right)t\\y = 10 + t\end{array} \right.\) và d2: mx + 2y – 14 = 0. Giá trị của m để hai đường thẳng trên song song với nhau là
Cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 8 - \left( {m + 1} \right)t\\y = 10 + t\end{array} \right.\) và d2: mx + 2y – 14 = 0. Giá trị của m để hai đường thẳng trên song song với nhau là
Câu 7:
Tìm các số thực a và b để cặp vectơ sau bằng nhau \(\overrightarrow x = \left( {a + b; - 2a + 3b} \right)\) và \(\overrightarrow y = \left( {2a - 3;\,4b} \right)\).
Tìm các số thực a và b để cặp vectơ sau bằng nhau \(\overrightarrow x = \left( {a + b; - 2a + 3b} \right)\) và \(\overrightarrow y = \left( {2a - 3;\,4b} \right)\).
Câu 9:
Tọa độ giao điểm của hai đường thẳng x – 3y – 6 = 0 và 3x + 4y – 1 = 0 là
Tọa độ giao điểm của hai đường thẳng x – 3y – 6 = 0 và 3x + 4y – 1 = 0 là
Câu 10:
Cho biểu thức (a + b)n , với n = 4 thì khi khai triển ta được một biểu thức có số số hạng là
Cho biểu thức (a + b)n , với n = 4 thì khi khai triển ta được một biểu thức có số số hạng là
Câu 12:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC?
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC?
Câu 13:
Cho tập hợp H = {1; 3; 5; 7; 9; 11}. Một tổ hợp chập 3 của 6 phần tử của H là
Cho tập hợp H = {1; 3; 5; 7; 9; 11}. Một tổ hợp chập 3 của 6 phần tử của H là
Câu 14:
Số hạng không chứa x trong khai triển nhị thức Newton của (2x – 5)5 là
Số hạng không chứa x trong khai triển nhị thức Newton của (2x – 5)5 là
Câu 15:
Cho đường thẳng ∆ đi qua điểm A(4; – 5) và có một vectơ pháp tuyến là \(\overrightarrow n = \left( {1;\,\,2} \right)\). Phương trình tham số của đường thẳng ∆ là
Cho đường thẳng ∆ đi qua điểm A(4; – 5) và có một vectơ pháp tuyến là \(\overrightarrow n = \left( {1;\,\,2} \right)\). Phương trình tham số của đường thẳng ∆ là


