Đề kiểm tra giữa học kì 2 Toán 10 Cánh Diều có đáp án
Đề kiểm tra giữa học kì 2 Toán 10 Cánh Diều - Đề 02 có đáp án
-
737 lượt thi
-
38 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
15/07/2024Nếu một công việc được hoàn thành bởi một trong ba hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện, hành động thứ ba có k cách thực hiện (các cách thực hiện của ba hành động là khác nhau đôi một) thì số cách hoàn thành công việc đó là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 2:
20/07/2024Nếu một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện, ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai, ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động số hai, có k cách thực hiện hành động số ba thì số cách hoàn thành công việc đó là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 3:
23/07/2024Cho tập A = {0; 1; 3; 5; 7}. Có thể lập được bao nhiêu số tự nhiên có 4 chữ số sao cho các chữ số đó đôi một khác nhau và là số chẵn.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì là số chẵn nên chữ số hàng đơn vị chỉ có thể là 0.
Chọn chữ số hàng nghìn có 4 cách chọn.
Chọn chữ số hàng trăm có 3 cách chọn.
Chọn chữ số hàng chục có 2 cách chọn.
Số số lập được là:
4 . 3 . 2 = 24 (số).
Câu 4:
13/07/2024Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:
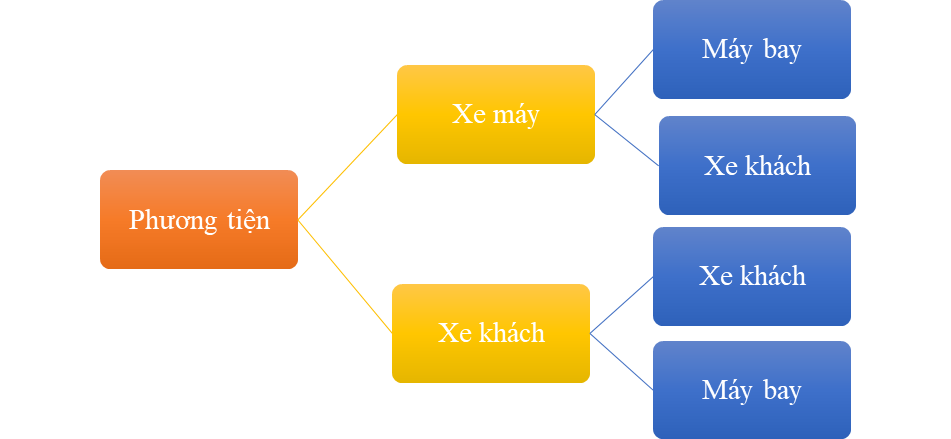
Hỏi bạn Khoa có mấy cách chọn phương tiện đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 5:
18/07/2024Cho tập A có n phần tử (n ∈ ℕ, n ≥ 2), k là số nguyên thỏa mãn 1 ≤ k ≤ n. Mỗi chỉnh hợp chập k của n phần tử đã cho là
 Xem đáp án
Xem đáp án
Đáp án C
Câu 7:
13/07/2024Cho k, n là các số nguyên dương, k ≤ n. Trong các phát biểu sau, phát biểu nào sai?
 Xem đáp án
Xem đáp án
Đáp án D
Câu 8:
17/07/2024Có bao nhiêu cách xếp 5 người ngồi vào một dãy ghế gồm có 6 chiếc ghế, biết mỗi người ngồi vào một ghế.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Mỗi cách sắp xếp 5 người vào dãy 6 ghế là một chỉnh hợp chập 5 của 6. Do đó, có số cách sắp xếp là \(A_6^5 = 720\) cách.
Câu 9:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xếp bạn Châu ngồi giữa có 1 cách.
Xếp 4 bạn sinh Anh, Chánh, Hằng, Loan vào 4 chỗ còn lại, mỗi cách xếp là một hoán vị của 4 phần tử nên có 4! = 24 cách.
Vậy có 1 . 24 = 24 cách xếp.
Câu 10:
20/07/2024Cho tập hợp H = {1; 3; 5; 7; 9; 11}. Một tổ hợp chập 3 của 6 phần tử của H là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 11:
23/07/2024Với n là số nguyên dương tùy ý lớn hơn 1, mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 12:
21/07/2024Một lớp có 40 học sinh gồm 25 nam và 15 nữ. Hỏi có bao nhiêu cách chọn ra một nhóm 3 học sinh trong đó có ít nhất một học sinh nữ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Chọn ra một nhóm gồm 3 học sinh bất kì trong 40 học sinh có \(C_{40}^3\) (cách chọn).
Chọn ra một nhóm gồm 3 học sinh toàn là nam có \(C_{25}^3\) (cách chọn).
Số cách chọn ra một nhóm 3 học sinh trong đó có ít nhất một học sinh nữ là:
\(C_{40}^3 - C_{25}^3 = 7580\) (cách chọn).
Câu 13:
21/07/2024Trong một hộp đựng 4 viên bi hồng và 3 viên bi tím. Lấy ngẫu nhiên ra 2 viên. Có bao nhiêu cách lấy được 2 viên bi cùng màu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Số cách lấy 2 viên bi cùng màu hồng là \(C_4^2 = 6\).
Số cách lấy 2 viên bi cùng màu tím là \(C_3^2 = 3\).
Như vậy, số cách lấy được hai viên bi cùng màu là: 6 + 3 = 9 (cách).
Câu 14:
19/07/2024Cho biểu thức (a + b)n , với n = 4 thì khi khai triển ta được một biểu thức có số số hạng là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 16:
14/07/2024Số hạng không chứa x trong khai triển nhị thức Newton của (2x – 5)5 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
(2x – 5)5
\( = C_5^0.{\left( {2x} \right)^5} + C_5^1.{\left( {2x} \right)^4}.\left( { - 5} \right) + C_5^2.{\left( {2x} \right)^3}.{\left( { - 5} \right)^2} + C_5^3.{\left( {2x} \right)^2}.{\left( { - 5} \right)^3} + C_5^4.\left( {2x} \right).{\left( { - 5} \right)^4} + C_5^5.{\left( { - 5} \right)^5}\)
= 32x5 – 400x4 + 2000x3 – 5000x2 + 6250x – 3125.
Do đó, số hạng không chứa x trong khai triển nhị thức Newton của (2x – 5)5 là – 3125.
Câu 17:
13/07/2024Trong mặt phẳng tọa độ Oxy, cho vectơ \(\overrightarrow a = - 2\overrightarrow i + 3\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow a \) là
 Xem đáp án
Xem đáp án
Đáp án C
Câu 18:
18/07/2024Trong mặt phẳng tọa độ Oxy, cho M(3; – 6) và N(5; 2). Tọa độ trung điểm I của MN là
 Xem đáp án
Xem đáp án
Đáp án A
Câu 19:
15/07/2024Trong mặt phẳng tọa độ Oxy, cho điểm H(1; 6). Tọa độ của vectơ \(\overrightarrow {OH} \) là
 Xem đáp án
Xem đáp án
Đáp án A
Câu 20:
22/07/2024Tìm các số thực a và b để cặp vectơ sau bằng nhau \(\overrightarrow x = \left( {a + b; - 2a + 3b} \right)\) và \(\overrightarrow y = \left( {2a - 3;\,4b} \right)\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(\overrightarrow x = \overrightarrow y \Leftrightarrow \left\{ \begin{array}{l}a + b = 2a - 3\\ - 2a + 3b = 4b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b = 3\\2a + b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\end{array} \right.\).
Câu 21:
18/07/2024Cho hình bình hành ABCD có A(– 1; – 2), B(3; 2), C(4; – 1). Tọa độ của đỉnh D là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l}3 - \left( { - 1} \right) = 4 - {x_D}\\2 - \left( { - 2} \right) = - 1 - {y_D}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 0\\{y_D} = - 5\end{array} \right.\).
Vậy D(0; – 5).
Câu 22:
21/07/2024Trong mặt phẳng tọa độ Oxy, cho A(2; 7) và B(– 2; 8). Độ dài đoạn thẳng AB là
 Xem đáp án
Xem đáp án
Đáp án C
Câu 23:
20/07/2024Cho hai vectơ \(\overrightarrow x = \left( {3;\, - 4} \right)\), \(\overrightarrow y = \left( { - 6;\,\,8} \right)\). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án C
Câu 24:
21/07/2024Trong mặt phẳng tọa độ Oxy, cho hai vectơ \(\overrightarrow a = \left( {4;\,\, - m} \right)\) và \(\overrightarrow b = \left( {2m + 6;\,\,1} \right)\). Tập giá trị của m để hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \overrightarrow a = k\overrightarrow b \)\( \Rightarrow \left\{ \begin{array}{l}4 = k\left( {2m + 6} \right)\\ - m = k\end{array} \right. \Rightarrow \left[ \begin{array}{l}m = - 1\\m = - 2\end{array} \right.\).
Câu 25:
13/07/2024Cho tam giác ABC có A(1; 2), B(– 1; 1), C(5; – 1). Tính \(\overrightarrow {AB} \cdot \overrightarrow {AC} \).
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(\overrightarrow {AB} = \left( { - 2;\,\, - 1} \right),\,\,\overrightarrow {AC} = \left( {4;\,\, - 3} \right)\).
Do đó, \(\overrightarrow {AB} \cdot \overrightarrow {AC} = \left( { - 2} \right) \cdot 4 + \left( { - 1} \right) \cdot \left( { - 3} \right) = - 8 + 3 = - 5\).
Câu 26:
23/07/2024Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: – x + 2y + 7 = 0. Vectơ pháp tuyến của đường thẳng d là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 27:
13/07/2024Phương trình tham số của đường thẳng ∆ đi qua điểm A(– 4; 2) và nhận \(\overrightarrow u = \left( {2;\,\, - 5} \right)\) làm vectơ chỉ phương là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 28:
19/07/2024Phương trình tổng quát của đường thẳng d đi qua điểm A(1; – 3) và nhận \(\overrightarrow n = \left( { - 2;\,\,7} \right)\) làm vectơ pháp tuyến là
 Xem đáp án
Xem đáp án
Đáp án C
Câu 29:
21/07/2024Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3; – 1) và B(– 6; 2). Phương trình nào sau đây không phải là phương trình tham số của đường thẳng AB?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Cách 1. Thay tọa độ các điểm A, B lần lượt vào các phương trình trong các đáp án thì thấy đáp án B không thỏa mãn.
Cách 2. Nhận thấy rằng các phương trình ở các đáp án A, C, D thì vectơ chỉ phương của các đường thẳng đó cùng phương, riêng chủ có đáp án B thì không. Do đó chọn đáp án B.
Câu 30:
19/07/2024Cho đường thẳng ∆ đi qua điểm A(4; – 5) và có một vectơ pháp tuyến là \(\overrightarrow n = \left( {1;\,\,2} \right)\). Phương trình tham số của đường thẳng ∆ là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Do đường thẳng ∆ có một vectơ pháp tuyến là \(\overrightarrow n = \left( {1;\,\,2} \right)\) nên đường thẳng ∆ có một vectơ chỉ phương là \(\overrightarrow u = \left( {2;\,\, - 1} \right)\).
Do đó, phương trình tham số của đường thẳng ∆ là \(\left\{ \begin{array}{l}x = 4 + 2t\\y = - 5 - t\end{array} \right.\).
Câu 32:
13/07/2024Góc giữa hai đường thẳng a: 6x – 5y + 15 = 0 và b: \(\left\{ \begin{array}{l}x = 10 - 6t\\y = 1 + 5t\end{array} \right.\) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Đường thẳng a có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {6;\,\, - 5} \right)\);
Đường thẳng b có một vectơ chỉ phương là \(\overrightarrow {{u_2}} = \left( { - 6;\,\,5} \right)\) nên nó có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {5;\,6} \right)\).
Ta thấy: \(\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} = 6 \cdot 5 + \left( { - 5} \right) \cdot 6 = 0\).
Suy ra góc giữa hai đường thẳng bằng 90°.
Câu 33:
21/07/2024Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(\overrightarrow {BC} = \left( {2;\,\,3} \right)\).
Đường cao kẻ từ A của tam giác ABC nhận \(\overrightarrow {BC} \) làm vectơ pháp tuyến và đi qua điểm A nên có phương trình là: 2(x – 1) + 3(y – 2) = 0 hay 2x + 3y – 8 = 0.
Câu 34:
15/07/2024Tọa độ giao điểm của hai đường thẳng x – 3y – 6 = 0 và 3x + 4y – 1 = 0 là
 Xem đáp án
Xem đáp án
Đáp án A
Câu 35:
21/07/2024Cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 8 - \left( {m + 1} \right)t\\y = 10 + t\end{array} \right.\) và d2: mx + 2y – 14 = 0. Giá trị của m để hai đường thẳng trên song song với nhau là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \({d_1}:\left\{ \begin{array}{l}x = 8 - \left( {m + 1} \right)t\\y = 10 + t\end{array} \right.\).
Từ đó suy ra, đường thẳng d1 đi qua điểm A(8; 10) và có một vectơ chỉ phương là \(\overrightarrow {{u_1}} = \left( { - m - 1;\,\,1} \right)\), do đó nó có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {1;\,\,m + 1} \right)\).
Ta có: d2: mx + 2y – 14 = 0.
Từ đó suy ra đường thẳng d2 có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {m;\,\,2} \right)\).
\({d_1}\,{\rm{//}}\,{d_2} \Leftrightarrow \left\{ \begin{array}{l}A \notin {d_2}\\\left[ \begin{array}{l}m = 0 \to \left\{ \begin{array}{l}\overrightarrow {{n_1}} = \left( {1;\,\,1} \right)\\\overrightarrow {{n_2}} = \left( {0;\,\,2} \right)\end{array} \right.(ktm)\\m \ne 0 \to \frac{1}{m} = \frac{{m + 1}}{2}\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8m + 6 \ne 0\\m \ne 0\\m\left( {m + 1} \right) = 2\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 2\end{array} \right.\).
Vậy m ∈ {– 2; 1} thì d1 // d2.
Câu 36:
22/07/2024Một nhóm học sinh gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một đội cờ đỏ sao cho phải có 1 đội trưởng nam, 1 đội phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập đội cờ đỏ?
 Xem đáp án
Xem đáp án
Vì trong 5 người được chọn phải có ít nhất 1 nữ và ít nhất phải có 2 nam nên số học sinh nữ gồm 1 hoặc 2 hoặc 3 nên ta có các trường hợp sau:
• Trường hợp 1: chọn 1 nữ và 4 nam.
+) Số cách chọn 1 nữ: 5 cách
+) Số cách chọn 2 nam làm đội trưởng và đội phó: \(A_{15}^2\)
+) Số cách chọn 2 nam còn lại: \(C_{13}^2\)
Suy ra có \(5A_{15}^2.C_{13}^2\) cách chọn cho trường hợp này.
• Trường hợp 2: chọn 2 nữ và 3 nam.
+) Số cách chọn 2 nữ: \(C_5^2\) cách.
+) Số cách chọn 2 nam làm đội trưởng và đội phó: \(A_{15}^2\)cách.
+) Số cách chọn 1 còn lại: 13 cách.
Suy ra có \[13A_{15}^2.C_5^2\] cách chọn cho trường hợp này.
• Trường hợp 3: Chọn 3 nữ và 2 nam.
+) Số cách chọn 3 nữ : \(C_5^3\) cách.
+) Số cách chọn 2 làm đội trưởng và đội phó: \(A_{15}^2\) cách.
Suy ra có \(A_{15}^2.C_5^3\) cách chọn cho trường hợp 3.
Vì các trường hợp là rời nhau. Vậy nên ta có \(5A_{15}^2.C_{13}^2 + 13A_{15}^2.C_5^2 + A_{15}^2.C_5^3 = 111\,300\) cách.
Câu 37:
16/07/2024Cho đường thẳng d1: 2x – y – 2 = 0; d2: x + y + 3 = 0 và điểm M(3; 0). Viết phương trình đường thẳng ∆ đi qua điểm M, cắt d1 và d2 lần lượt tại A và B sao cho M là trung điểm của đoạn AB.
 Xem đáp án
Xem đáp án
Gọi tọa độ các điểm A, B và M là A(xA; yA); B(xB; yB) và M(xM; yM).
Vì A thuộc d1 nên 2xA – yA – 2 = 0. Suy ra yA = 2xA – 2.
Vì B thuộc d2 nên xB + yB + 3 = 0. Suy ra yB = – xB – 3.
Do M là trung điểm của đoạn AB nên
\(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}\\{y_A} + {y_B} = 2{y_M}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 6\\\left( {2{x_A} - 2} \right) + \left( { - {x_B} - 3} \right) = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} = \frac{{11}}{3}\\{y_A} = \frac{{16}}{3}\end{array} \right.\).
Suy ra \(A\left( {\frac{{11}}{3};\,\,\frac{{16}}{3}} \right)\).
Đường thẳng ∆ đi qua điểm A và điểm M.
Ta có: \(\overrightarrow {AM} = \left( { - \frac{2}{3};\,\, - \frac{{16}}{3}} \right)\)\( \Rightarrow \overrightarrow {{u_{AM}}} = \left( {1;\,\,8} \right) \Rightarrow \overrightarrow {{n_{AM}}} = \left( {8;\,\, - 1} \right)\).
Đường thẳng ∆ đi qua M(3; 0) và có một vectơ pháp tuyến là \(\overrightarrow {{n_{AM}}} \) nên có phương trình là
8(x – 3) – (y – 0) = 0 hay 8x – y – 24 = 0.
Câu 38:
20/07/2024Cho n là số tự nhiên. Hãy tính tổng sau:
S = \(C_{2n + 1}^0 + C_{2n + 1}^1 + C_{2n + 1}^2 + ... + C_{2n + 1}^n\).
 Xem đáp án
Xem đáp án
Ta có: S = \(C_{2n + 1}^0 + C_{2n + 1}^1 + C_{2n + 1}^2 + ... + C_{2n + 1}^n\)
Suy ra 2S = \[\left[ {C_{2n + 1}^0 + C_{2n + 1}^1 + C_{2n + 1}^2 + ... + C_{2n + 1}^n} \right]\] + \(\left[ {C_{2n + 1}^0 + C_{2n + 1}^1 + C_{2n + 1}^2 + ... + C_{2n + 1}^n} \right]\)
Lại có: \(C_n^k = C_n^{n - k}\) (tính chất tổ hợp).
Do đó, 2S = \[\left[ {C_{2n + 1}^0 + C_{2n + 1}^1 + C_{2n + 1}^2 + ... + C_{2n + 1}^n} \right]\] + \[\left[ {C_{2n + 1}^{2n + 1} + C_{2n + 1}^{2n} + C_{2n + 1}^{2n - 1} + ... + C_{2n + 1}^{n + 1}} \right]\]
⇒ 2S = \[C_{2n + 1}^0 + C_{2n + 1}^1 + C_{2n + 1}^2 + ... + C_{2n + 1}^n\]\[ + C_{2n + 1}^{n + 1} + ... + C_{2n + 1}^{2n - 1} + C_{2n + 1}^{2n} + C_{2n + 1}^{2n + 1}\]
Xét khai triển (1 + x)2n + 1 = \[C_{2n + 1}^0{x^0} + C_{2n + 1}^1{x^1} + ... + C_{2n + 1}^{2n}{x^{2n}} + C_{2n + 1}^{2n + 1}{x^{2n + 1}}\].
Khi x = 1 ⇒ 2S = 22n + 1 ⇒ S = 22n = 4n.
Vậy S = 4n.
Bài thi liên quan
-
Đề kiểm tra giữa học kì 2 Toán 10 Cánh Diều - Đề 01 có đáp án
-
38 câu hỏi
-
50 phút
-
Có thể bạn quan tâm
- Đề kiểm tra giữa học kì 2 Toán 10 Cánh Diều có đáp án (736 lượt thi)
- Đề kiểm tra cuối học kì 2 Toán 10 Cánh Diều có đáp án (888 lượt thi)
Các bài thi hot trong chương
- Đề thi Học kì 1 Toán 10 Cánh diều có đáp án (519 lượt thi)
- Đề thi Giữa kì 1 Toán 10 Cánh diều có đáp án (487 lượt thi)
