Khối lập phương là khối đa diện đều loại

Đáp án đúng là C

*Lời giải

Khối lập phương là khối đa diện đều loại {4;3} 

Khối lập phương thuộc loại khối đa diện đều mà mỗi mặt là đa giác đều có 4 cạnh và mỗi đỉnh là đỉnh chung của 3 mặt.

*Phương pháp giải

Một khối đa diện lồi được gọi là khối đa diện đều loại {p,q}

- Mỗi mặt của nó là một đa giác đều p cạnh

- Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.

*Lý thuyến cần nắm và dạng toán về khối đa diện:

- Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.

- Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện.

Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.

- Mỗi hình đa diện chia các điểm còn lại của không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện, trong đó chỉ có miền ngoài là chứa hoàn toàn một đường thẳng nào đấy.

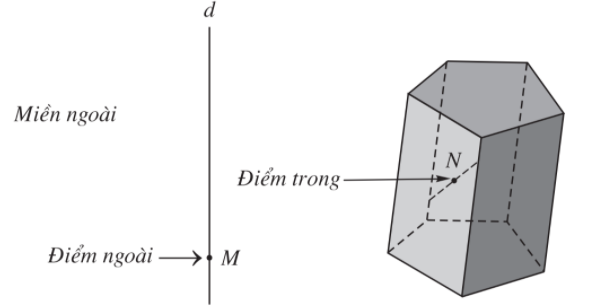
Khối đa diện đều.

- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:

a) Mỗi mặt của nó là một đa giác đều p cạnh.

b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.

Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.

Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.

- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.

Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.

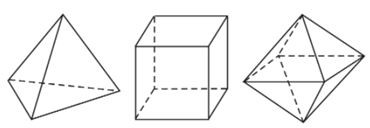
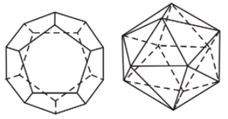
Bảng tóm tắt của năm loại khối đa diện đều.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Khối đa diện lồi và khối đa diện đều

50 Bài tập Khái niệm về khối đa diện

50 bài toán về thể tích khối đa diện (có đáp án 2024) – Toán 12