Câu hỏi:
23/10/2024 177Hình chóp tam giác có số cạnh là
A. 5
B. 3
C. 6
D. 4
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: C
*Phương pháp giải:
- dựa vào lý thuyết của hình chóp tam giác để suy ra số cạnh (cạnh bên & cạnh đáy)
*Lời giải:
Số cạnh của một hình chóp bằng hai lần số cạnh đáy của hình chóp đó
Vậy số cạnh của hình chóp tam giác: 6 ( 3 cạnh bên và 3 cạnh đáy(đáy là tam giác))
*Lý thuyết cần nắm và diện tích xung quanh, thể tích của hình chóp tam giác, hình chóp tứ giác:
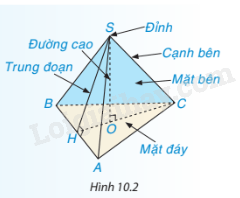
Hình chóp tam giác đều có:
- Đáy là tam giác đều.
- 3 cạnh bên bằng nhau.
- 3 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 3 cạnh đáy bằng nhau là ba cạnh của tam giác đáy.
- Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm cách đều các đỉnh của tam giác đáy.
a. Diện tích xung quanh của hình chóp tam giác đều
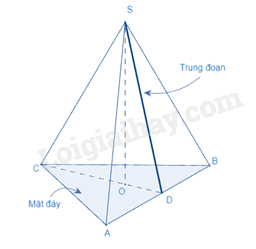
Diện tích xung quanh, kí hiệu là của hình chóp tam giác đều được tính theo công thức:
,
trong đó p là nửa chu vi đáy, d là trung đoạn.
b. Thể tích của hình chóp tam giác đều
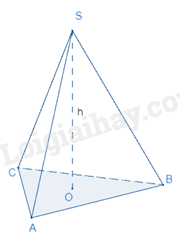
Thể tích của hình chóp tam giác đều bằng diện tích đáy nhân với chiều cao.
trong đó V là thể tích,
S là diện tích đáy,
h là chiều cao.
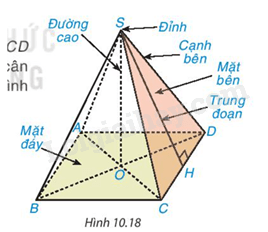
Hình chóp tứ giác đều có:
- Đáy là hình vuông.
- 4 cạnh bên bằng nhau.
- 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.
- Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm cách đều các đỉnh của mặt đáy (giao điểm hai đường chéo)
a. Diện tích xung quanh của hình chóp tứ giác đều
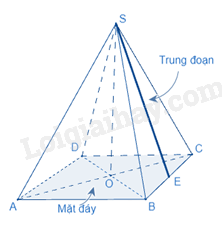
Diện tích xung quanh, kí hiệu là của hình chóp tứ giác đều được tính theo công thức:
,
trong đó p là nửa chu vi đáy,
d là trung đoạn.
b. Thể tích của hình chóp tứ giác đều
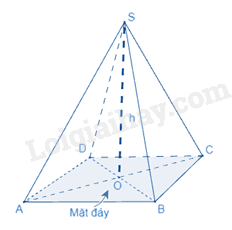
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng diện tích đáy nhân với chiều cao.
trong đó V là thể tích,
S là diện tích đáy,
h là chiều cao.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Hình chóp tam giác đều – Toán lớp 8 Kết nối tri thức
TOP 40 câu Trắc nghiệm Hình chóp đều và hình chóp cụt đều (có đáp án 2023) - Toán 8
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số có đạo hàm liên tục trên khoảng và thỏa mãn ; biết . Giá trị f(2) thuộc khoảng nào dưới đây?
Câu 3:
Biết rằng giá trị lớn nhất của hàm số trên đoạn [-2;1] đạt giá trị nhỏ nhất, giá trị của tham số m bằng
Câu 4:
Trong không gian Oxyz, cho đường thẳng . Phương trình nào dưới đây là phương trình của đường thẳng vuông góc với d?
Câu 6:
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn . Tổng phần thực và phần ảo của số phức z bằng
Câu 7:
Trong không gian Oxyz, cho mặt cầu và hai điểm A(5;10;0), B(4;2;1). Gọi M là điểm thuộc mặt cầu (S). Giá trị nhỏ nhất của MA + 3MB bằng
Câu 8:
Cho hàm số liên tục trên đoạn [a;b], có đồ thị tạo với trục hoành một hình phẳng gồm ba phần có diện tích như hình vẽ.
![Cho hàm số y = f(x) liên tục trên đoạn [a;b], có đồ thị tạo với trục hoành một hình phẳng gồm ba phần có diện tích s1, s2, s3 như hình vẽ (ảnh 1)](https://vietjack.me/storage/uploads/images/233/zzs27-1651503093.png)
Tích phân bằng
Câu 9:
Trong không gian Oxyz, cho mặt phẳng (P): 2x - 2y - z + 2 = 0. Khoảng cách từ điểm M(1;-1;-3) đến (P) bằng
Câu 10:
Trong không gian Oxyz, cho hai đường thẳng , và mặt phẳng . Đường thẳng vuông góc với , cắt cả và có phương trình là:
Câu 11:
Cho hàm số liên tục trên và có đồ thị như hình vẽ bên
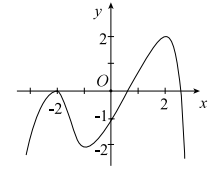
Tập hợp nghiệm của phườn trình có bao nhiêu phần tử?
Câu 12:
Gọi là nghiệm phức có phần ảo âm của phương trình . Trên mặt phẳng tọa độ, điểm biểu diễn có tọa độ là
Câu 14:
Tổng giá trị lớn nhất và nhỏ nhất của biểu thức bằng bao nhiêu, biết rằng x, y, z là các số thực thỏa mãn .



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)