Câu hỏi:
30/10/2024 1,430Góc lượng giác có số đo α (rad) thì mọi góc lượng giác cùng tia đầu và tia cuối với nó có số đo dạng :
A. α + k.1800 ( k là số nguyên)
B. α + k. 3600 (k là số nguyên).
C. α + k2π ( k là số nguyên).
D. α + kπ ( k là số nguyên).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: C.
* Lời giải:
Nếu một góc lượng giác (Ou; Ov) có số đo α radian thì mọi góc lượng giác cùng tia đầu Ou, tia cuối Ov có số đo α + 2kπ, k ∈ Z, mỗi góc tương ứng với một giá trị của k.
Các cung lượng giác tương ứng trên đường tròn định hướng tâm O cũng có tính chất như vậy.
* Phương pháp giải:
- vận dụng kiến thức về góc lượng giác tia đầu và tia cuối. biết số đo góc lượng giác bằng α
* Lý thuyết và các dạng bài về góc và cung lượng giác:
Công thức nhân đôi:
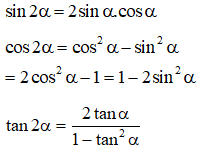
* Công thức hạ bậc:
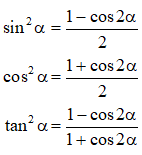
Phương trình lượng giác cơ bản
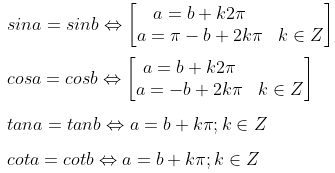
Phương trình lượng giác đặc biệt
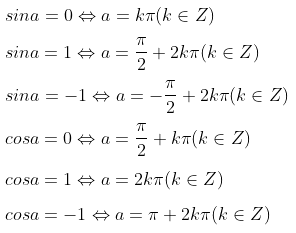
Xem thêm các bài viết liên quan hay, chi tiết:
Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhất
Giải Toán 10 Chương 6: Cung và góc lượng giác. Công thức lượng giác
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tính giá trị biểu thức sau: A = sin230 + sin2150 + sin2750 + sin2870
Câu 3:
Tính giá trị biểu thức sau: C = sin2450 - 2 sin2500 + 3cos2450 - 2sin2400 + 4tan550.tan350
Câu 7:
Cho hai góc lượng giác có sđ (Ox; Ou) = 450 + m.3600 và sđ (Ox; Ov) = -1350+ n. 360 0. Ta có hai tia Ou và Ov
Câu 10:
Tính giá trị biểu thức sau: B = 3 - sin2900 + 2cos2600 - 3tan2450
Câu 11:
Tính giá trị biểu thức sau: A = a2 sin900 + b2.cos900 + c2. cos1800
Câu 15:
Điểm cuối của α thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai ?


