Câu hỏi:
22/07/2024 216Đỉnh của parabol y =x2+x+m nằm trên đường thẳng y= 3/4 nếu m bằng:
A. 2.
B. 3.
C. 5.
D. 1.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Ta tìm đỉnh của parabol:
Suy ra m=1.
Chọn D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Giá trị nào của m thì đồ thị hàm số y= x2+ 3x+m cắt trục hoành tại hai điểm phân biệt?
Câu 2:
Nếu hàm số y= ax2+ bx+c có đồ thị như sau thì dấu các hệ số của nó là:
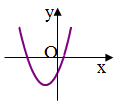
Câu 3:
Cho hàm số y=f(x) = ax2+ bx+c. Biểu thức f(x+ 3) -3f( x+ 2) +3f( x+ 1) có giá trị bằng.
Câu 4:
Parabol (P) có phương trình y= -x2 đi qua A và B có hoành độ lần lượt là và .Cho O là gốc tọa độ. Khi đó:
Câu 6:
Xác định parabol (P) ; y= ax2+bx+ c biết (P) đi qua M(4;3) cắt Ox tại N(3;0) và P sao cho ∆ INP có diện tích bằng 1 biết hoành độ điểm P nhỏ hơn 3.
Câu 7:
Cho đường thẳng d:(9m2-4) x+(n2-9) y=(n-3 )(3m+2). Với giá trị nào của m và n thì phương trình đã cho là đường thẳng song song với trục Ox?
Câu 8:
Cho parabol (P) ; y= ax2+bx+ c biết: (P) đi qua A(2;3) có đỉnh I( 1;2) . Hỏi a+ b+c bằng bao nhiêu.
Câu 10:
Parabol (P) y= m2x2 và đường thẳng (d) y= -4x-1 cắt nhau tại hai điểm phân biệt ứng với:
Câu 12:
Xác định parabol (P) ; y= ax2+bx+ c biết: Hàm số y= ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng khi x=1.
Câu 13:
Tìm giá trị nhỏ nhất và lớn nhất của các hàm số đó trên [ -2; 2]
Câu 14:
Cho phương trình x2+ 2( m+ 3) x+ m2-3=0, m là tham số.
Tìm m để phương trình có hai nghiệm x1; x2 và P = 5( x1+ x2) – 2x1.x2 giá trị lớn nhất.
Câu 15:
Tìm m để đường thẳng y= m cắt đồ thị hàm số tại điểm một điểm duy nhất.


