Câu hỏi:
05/11/2024 1,098
Có bao nhiêu vectơ pháp tuyến của một đường thẳng?
Có bao nhiêu vectơ pháp tuyến của một đường thẳng?
A. 0;
A. 0;
B. 1;
B. 1;
C. 2;
D. Vô số.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
*Phương pháp giải:
Nếu là vectơ pháp tuyến của đường thẳng thì k(k ≠ 0) cũng là vectơ pháp tuyến của đường thẳng đó. Do đó một đường thẳng có vô số vectơ pháp tuyến.
*Lý thuyết
I. Vecto pháp tuyến của mặt phẳng.
1. Định nghĩa:
Cho mặt phẳng (α). Nếu vecto và có giá vuông góc với mặt phẳng (α) thì được gọi là vecto pháp tuyến của (α)
2. Chú ý. Nếu là vecto pháp tuyến của một mặt phẳng thì cũng là vecto pháp tuyến của mặt phẳng đó.
3. Tích có hướng của hai vectơ
- Định nghĩa: Trong không gian Oxyz, cho hai vectơ , . Tích có hướng của hai vectơ và kí hiệu là , được xác định bởi
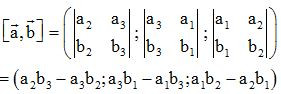
- Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.
Xem thêm
Cách tìm vecto pháp tuyến của đường thẳng (hay, chi tiết)
120 câu trắc nghiệm Phương pháp tọa độ trong mặt phẳng nâng cao
Hướng dẫn giải
Đáp án đúng là: D
*Phương pháp giải:
Nếu là vectơ pháp tuyến của đường thẳng thì k(k ≠ 0) cũng là vectơ pháp tuyến của đường thẳng đó. Do đó một đường thẳng có vô số vectơ pháp tuyến.
*Lý thuyết
I. Vecto pháp tuyến của mặt phẳng.
1. Định nghĩa:
Cho mặt phẳng (α). Nếu vecto và có giá vuông góc với mặt phẳng (α) thì được gọi là vecto pháp tuyến của (α)
2. Chú ý. Nếu là vecto pháp tuyến của một mặt phẳng thì cũng là vecto pháp tuyến của mặt phẳng đó.
3. Tích có hướng của hai vectơ
- Định nghĩa: Trong không gian Oxyz, cho hai vectơ , . Tích có hướng của hai vectơ và kí hiệu là , được xác định bởi
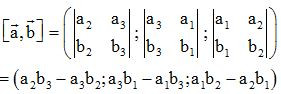
- Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.
Xem thêm
Cách tìm vecto pháp tuyến của đường thẳng (hay, chi tiết)
120 câu trắc nghiệm Phương pháp tọa độ trong mặt phẳng nâng cao
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho đường thẳng ∆ có một vectơ chỉ phương là . Vectơ nào dưới đây không phải là vectơ pháp tuyến của ∆.
Cho đường thẳng ∆ có một vectơ chỉ phương là . Vectơ nào dưới đây không phải là vectơ pháp tuyến của ∆.
Câu 2:
Vectơ chỉ phương của đường thẳng đi qua hai điểm A(2; 3) và B(4; 1) là:
Câu 3:
Cho đường thẳng (d): 2x + 3y – 4 = 0. Vectơ nào sau đây là vectơ pháp tuyến của (d)?
Cho đường thẳng (d): 2x + 3y – 4 = 0. Vectơ nào sau đây là vectơ pháp tuyến của (d)?
Câu 4:
Phương trình tham số của đường thẳng d đi qua điểm A(2; 3) và nhận làm vectơ chỉ phương là:
Phương trình tham số của đường thẳng d đi qua điểm A(2; 3) và nhận làm vectơ chỉ phương là:
Câu 5:
Cho đường thẳng ∆: 3x – 4y + 5 = 0. Hệ số góc của đường thẳng d là:
Cho đường thẳng ∆: 3x – 4y + 5 = 0. Hệ số góc của đường thẳng d là:


