Câu hỏi:
18/07/2024 140
Cho tứ giác ABCD, I là trung điểm BD. Tìm điểm O thỏa mãn →OB+4→OC=2→OD
Cho tứ giác ABCD, I là trung điểm BD. Tìm điểm O thỏa mãn →OB+4→OC=2→OD
A. O là đỉnh của hình bình hành IBON với →IN=53→IC;
B. O là đỉnh của hình bình hành IBON với →IN=43→IC;
C. O là đỉnh của hình bình hành IBON với →IN=→IC;
D. O là đỉnh của hình bình hành IBON với →IN=23→IC.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
→OB+4→OC=2→OD
⇔→OB+4(→OB+→BC)=2(→OB+→BD) (quy tắc ba điểm)
⇔3→OB=2→BD−4→BC
⇔3→OB=2(→BD−→BC)−2→BC (quy tắc trừ hai vectơ)
⇔3→OB=2→BD−4→BC
⇔3→OB=2→BD+4→CB
⇔3→OB=2(→CB+→BD)+2→CB
⇔3→OB=2→CD+2→CB (quy tắc ba điểm)
⇔3→OB=4→CI (do I là trung điểm của BD nên →CD+→CB=2→CI)
⇔→OB=43→CI
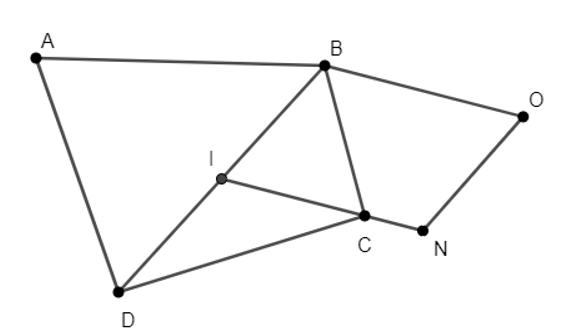
Vậy O là đỉnh của hình bình hành IBON với →IN=43→IC.
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
→OB+4→OC=2→OD
⇔→OB+4(→OB+→BC)=2(→OB+→BD) (quy tắc ba điểm)
⇔3→OB=2→BD−4→BC
⇔3→OB=2(→BD−→BC)−2→BC (quy tắc trừ hai vectơ)
⇔3→OB=2→BD−4→BC
⇔3→OB=2→BD+4→CB
⇔3→OB=2(→CB+→BD)+2→CB
⇔3→OB=2→CD+2→CB (quy tắc ba điểm)
⇔3→OB=4→CI (do I là trung điểm của BD nên →CD+→CB=2→CI)
⇔→OB=43→CI

Vậy O là đỉnh của hình bình hành IBON với →IN=43→IC.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tứ giác ABCD. Gọi I là trung điểm của BC. Xác định điểm M sao cho: 2→MA+→MB+→MC=→0.
Cho tứ giác ABCD. Gọi I là trung điểm của BC. Xác định điểm M sao cho: 2→MA+→MB+→MC=→0.
Câu 2:
Cho tứ giác ABCD. Gọi G là trọng tâm của tam giác BCD. Xác định điểm P sao cho: →PB+→PC+→PD=3→AP.
Cho tứ giác ABCD. Gọi G là trọng tâm của tam giác BCD. Xác định điểm P sao cho: →PB+→PC+→PD=3→AP.
Câu 3:
Cho tứ giác ABCD và điểm O bất kì sao cho →OB+4→OC−2→OD=→0. Tìm điểm M thỏa mãn hệ thức |→MB+4→MC−2→MD|=|3→MA|.
Cho tứ giác ABCD và điểm O bất kì sao cho →OB+4→OC−2→OD=→0. Tìm điểm M thỏa mãn hệ thức |→MB+4→MC−2→MD|=|3→MA|.
Câu 5:
Cho tứ giác ABCD. Gọi K, H lần lượt là trung điểm của AB, CD. Xác định điểm N sao cho: →NA+→NB+→NC+→ND=→0.
Cho tứ giác ABCD. Gọi K, H lần lượt là trung điểm của AB, CD. Xác định điểm N sao cho: →NA+→NB+→NC+→ND=→0.
Câu 7:
Cho tam giác ABC vuông tại A. Điểm M bất kì nằm trong tam giác có hình chiếu xuống BC, CA, AB theo thứ tự là D, E, F. Tìm tập hợp điểm M biết →MD+→ME+→MF cùng phương với →BC.
Cho tam giác ABC vuông tại A. Điểm M bất kì nằm trong tam giác có hình chiếu xuống BC, CA, AB theo thứ tự là D, E, F. Tìm tập hợp điểm M biết →MD+→ME+→MF cùng phương với →BC.
Câu 9:
Cho tam giác ABC. Điểm P thỏa mãn →CP=→KA+2→KB−3→KC với K tùy ý là điểm thỏa mãn:
Cho tam giác ABC. Điểm P thỏa mãn →CP=→KA+2→KB−3→KC với K tùy ý là điểm thỏa mãn:


