Câu hỏi:
11/10/2024 2,679Cho hàm số Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
B. Hàm số nghịch biến trên khoảng
C. Hàm số đồng biến trên khoảng
D. Hàm số nghịch biến trên khoảng
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: B.
*Phương pháp giải:
- Tìm tập xác định của hàm số
- Tính đạo hàm của hàm số
- xét dấu trên bảng để tìm ra khoảng nghịch biến
*Lời giải:
TXĐ:
Ta có
Bảng xét dấu y' như sau:
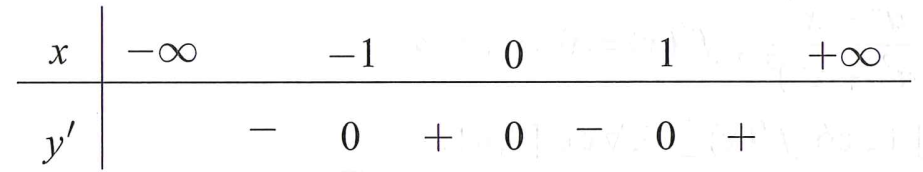
Dựa vào bảng xét dấu, suy ra hàm số đã cho nghịch biến trên các khoảng và (0;1) nên nghịch biến trên khoảng
*Cách tìm khoảng đồng biến/nghịch biến của hàm số:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K ta có:
+ Hàm số y = f(x) được gọi là hàm số đồng biến B (tăng) trên K nếu với mọi x1, x2 thuộc K và x1 < x2 thì f(x1) < f(x2).
+ Hàm số y = f(x) được gọi là hàm số nghịch biến (giảm) trên K nếu với mọi x1, x2 thuộc K và x1 < x2 thì f(x1) > f(x2).
Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.
Nhận xét:
+ Hàm số f(x) đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Hàm số f(x) nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.

Các bước để xét tính đơn điệu của hàm số y = f(x):
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính đạo hàm f'(x). Tìm các điểm xi (i = 1, 2, …) tại đó đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên (hoặc bảng xét dấu đạo hàm) của hàm số.
Bước 4. Kết luận về các khoảng đồng biến và nghịch biến của hàm số.
Xem thêm các bài viết liên quan hay, chi tiết:
TOP 30 Đề thi Học kì 1 Toán 12 có đáp án
Bài tập về sự đồng biến và nghịch biến của hàm số (có đáp án)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABC có SA = SB = SC = BA = BC = 1. Tìm thể tích lớn nhất của khối chóp S.ABC?
Câu 3:
Cho phương trình với m là tham số thực. Tìm tất cả các giá trị của m để phương trình có đúng hai nghiệm phân biệt.
Câu 6:
Cho hàm số bậc bốn y = f(x) có đồ thị như hình vẽ dưới đây.
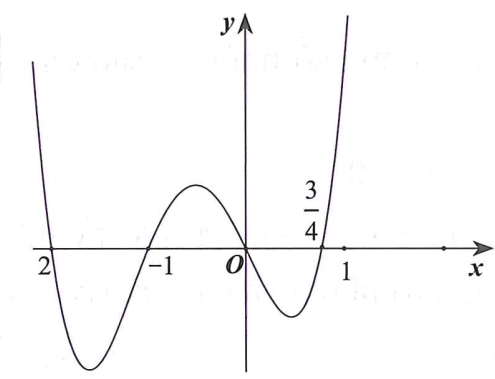
Số điểm cực trị của hàm số là
Câu 8:
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A(1;2;-3) có vectơ pháp tuyến là
Câu 9:
Phương trình bậc hai nào dưới đây nhận hai số phức 2 - 3i và 2 + 3i làm nghiệm?
Câu 10:
Hệ thức liên hệ giữa giá trị cực đại và giá trị cực tiểu của hàm số là
Câu 11:
Cho các số thực a, b (với a < b). Nếu hàm số y = f(x) có đạo hàm là hàm liên tục trên thì
Câu 12:
Cho hàm số (với m là tham số). Tìm tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên từng khoảng xác định.
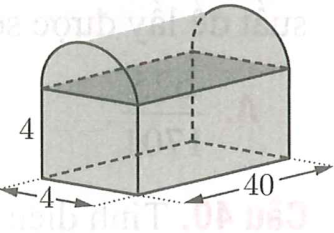
Câu 14:
Một thùng đựng thư được thiết kế như hình vẽ bên, phần phía trên là nửa hình trụ. Thể tích của thùng đựng thư bằng
Câu 15:
Cho hàm số y = f(x). Hàm số y = f'(x) có bảng biến thiên:
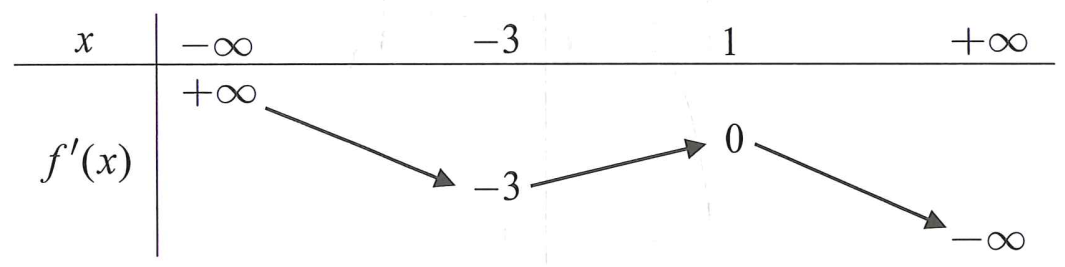
Bất phương trình nghiệm đúng với mọi khi và chỉ khi



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)