TOP 30 Đề thi Học kì 1 Toán 12 năm 2023 có đáp án
Bộ đề thi Học kì 1 Toán lớp 12 năm 2023 có đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 12 Học kì 1. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi Học kì 1 Toán 12 bản word có lời giải chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận đề thi.
Xem thử tài liệu tại đây: Link tài liệu
TOP 30 Đề thi Học kì 1 Toán lớp 12 năm 2023 có đáp án
Đề thi Học kì 1 Toán lớp 12 có đáp án - đề số 1
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học ...
Môn: Toán 12
Thời gian làm bài: 90 phút
PHẦN I: PHẦN TRẮC NGHIỆM
Câu 1. Hàm số có đồ thị là hình nào sau đây?
A. 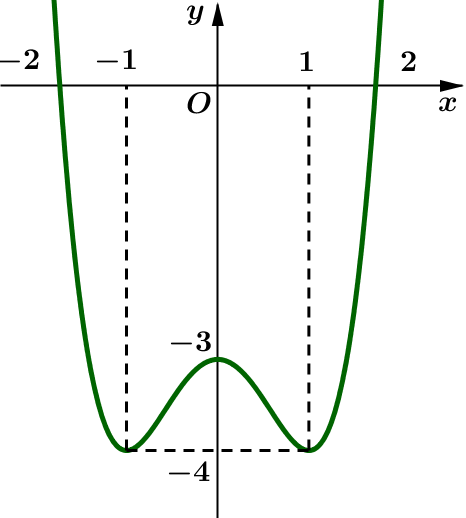
B. 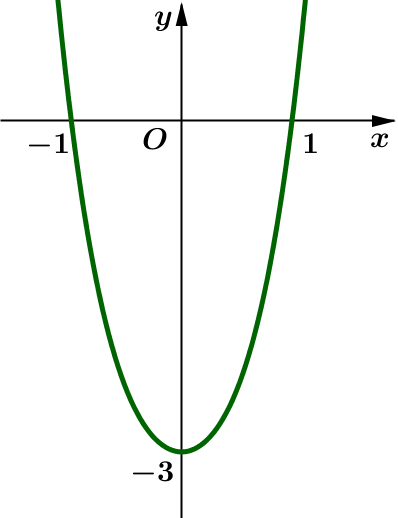 .
.
C. 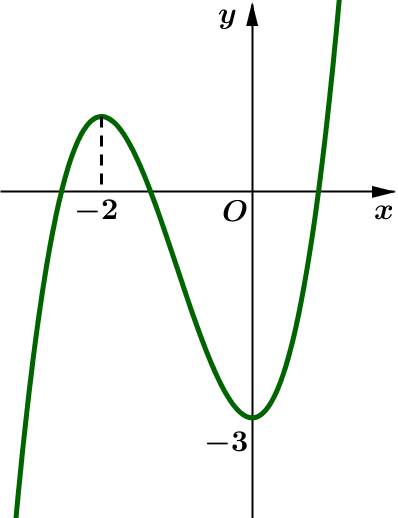
D. 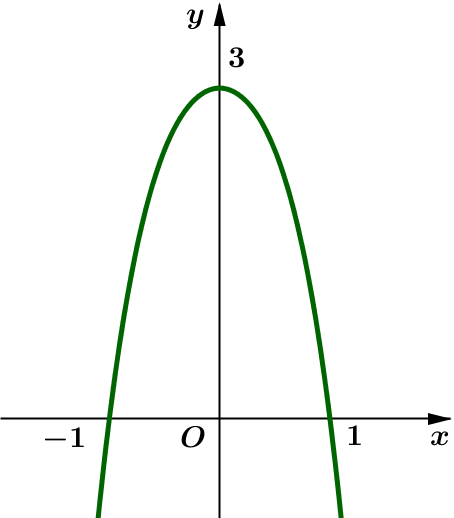 .
.
Câu 2. Bảng biến thiên dưới là của hàm số . Mệnh đề nào sau đây đúng
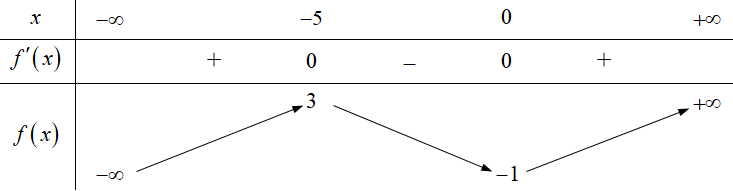
A. Hàm số đồng biến trên và .
B. Hàm số nghịch biến trên .
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên .
Câu 3. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số ?
A. .
B.
C. .
D. .
Câu 4. Tìm tập xác định của hàm số .
A. .
B. .
C. .
D. .
Câu 5. Hàm số có bao nhiêu điểm cực trị?
A. 0.
B. 1.
C. 2.
D. 3.
Câu 6. Cho , . Khẳng định nào sau đây đúng?
A.
B. .
C.
D. .
Câu 7. Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số và đối xứng nhau qua trục hoành.
B. Đồ thị hàm số và đối xứng nhau qua trục tung.
C. Đồ thị hàm số và đối xứng nhau qua đường thẳng
D. Đồ thị hàm số và đối xứng nhau qua đường thẳng
Câu 8. Cho các khẳng định sau:
(I). Hình chóp đều là hình chóp có đáy là đa giác đều và đường cao hạ từ đỉnh qua tâm của đáy.
(II). Hình hộp là lăng trụ có đáy là hình chữ nhật.
(III). Lăng trụ đều là lăng trụ đứng có đáy là đa giác đều.
(IV). Hình lập phương có 9 mặt phẳng đối xứng.
Số khẳng định đúng là?
A. 1
B. 2
C. 3
D. 4.
Câu 9. Cho các khẳng định sau:
(I). Tứ diện đều có 6 mặt phẳng đối xứng.
(II). Hình hộp chữ nhật kích thước khác nhau có 3 mặt phẳng đối xứng.
(III). Lăng trụ tam giác đều có 4 mặt phẳng đối xứng.
(IV). Bát diện đều có 9 mặt phẳng đối xứng.
Số khẳng định Sai là?
A. 0.
B. 1.
C. 2.
D. 3.
Câu 10. Thể tích khối nón tròn xoay có đường cao h, đường sinh l, bán kính đáy R có
thể tích là.
A. .
B. .
C. .
D. .
Câu 11. Đồ thị của hàm số và đường thẳng có tất cả bao
nhiêu điểm chung?
A. 4.
B. 2.
C. 1.
D. 3.
Câu 12. Tính đạo hàm của hàm số .
A. .
B. .
C. .
D. .
Câu 13. Tìm giá trị nhỏ nhất của hàm số trên đoạn .
A. .
B. .
C. .
D. .
Câu 14. Biết , thì tính theo a và b bằng
A. .
B. .
C. .
D. .
Câu 15. Tìm tất cả các giá trị thực của tham số m để hàm số
luôn đồng biến trên tập xác định của nó?
A. .
B. .
C. .
D. .
Câu 16. Cho hàm số . Có tất cả bao nhiêu giá trị thực của tham số m để đồ thị của hàm số đã cho có đúng một đường tiệm cận đứng?
A. 3.
B. 2.
C. 1.
D. 0.
Câu 17. Tìm tất cả các giá trị thực của tham số để giá trị lớn nhất của hàm số
trên đoạn bằng 2?
A. .
B. .
C.
D. .
Câu 18. Cho hàm số có đồ thị là đường cong như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
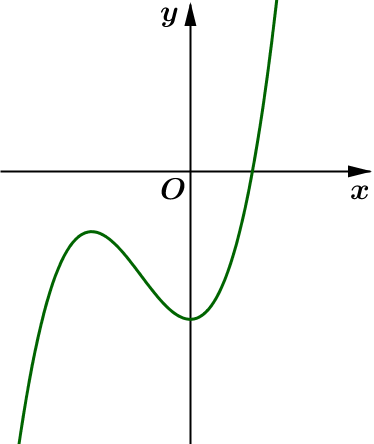
A.
B. .
C. .
D. .
Câu 19. Tìm tập nghiệm S của bất phương trình .
A. .
B.
C. .
D. .
Câu 20. Phương trình có 2 nghiệm trong đó . Chọn
phát biểu đúng?
A.
B.
C. .
D. .
Câu 21. Tìm tất cả các giá trị thực của tham số m sao cho hàm số có tập xác định .
A. .
B. .
C. hoặc .
D. .
Câu 22. Tìm m để phương trình có 2 nghiệm.
A. .
B. .
C. hoặc .
D. hoặc .
Câu 23. Trong các khẳng định sau, khẳng định nào đúng?
A. , .
B. , , .
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên khoảng .
Câu 24. Giải bất phương trình ta được bao nhiêu
nghiệm nguyên?
A. 4.
B. 5.
C. 6.
D. Vô số.
Câu 25. Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a. Thể tích của
(H) bằng.
A. .
B. .
C. .
D. .
Câu 26. Một hình trụ có bán kính đáy bằng 2 và có chiều cao bằng 4. Thể tích của
hình trụ bằng:
A. .
B. .
C. .
D. .
Câu 27. Cho một khối lăng trụ tam giác đều có thể tích là . Tính thể tích của khối trụ ngoại tiếp lăng trụ đã cho.
A. .
B. .
C. .
D. .
Câu 28. Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền .
Diện tích xung quanh của hình nón là.
A. .
B. .
C. .
D. .
Câu 29. Tính thể tích V của khối lập phương , biết tổng diện tích các
mặt của hình lập phương bằng 150.
A. .
B. .
C. .
D. .
Câu 30. Cho hình chóp có đáy là hình chữ nhật, ; ;
và . Thể tích của khối chóp S.SBCD bằng.
A. .
B. .
C.
D. .
Câu 31. Tìm tất cả các giá trị của tham số m để đồ thị hàm số
có hai điểm cực trị A và B, sao cho đường thẳng AB vuông
góc với đường thẳng .
A. và .
B. , và m = -2.
C. và .
D. , m = 1 và .
Câu 32. Phương trình có hai nghiệm ,
khi đó bằng bao nhiêu?
A.
B.
C. .
D. .
Câu 33. Tìm các giá trị của tham số m để hàm số nghịch biến trên khoảng .
A. .
B. .
C. .
D. .
Câu 34. Cho lăng trụ có thể tích V và một điểm M di động trong tam
giác A'B'C'. Khi đó thể tích khối chóp M.ABC tính theo V bằng.
A. .
B. .
C. .
D. .
Câu 35. Cho hình chóp có đáy ABCD là hình vuông cạnh a, hai mặt bên
và cùng vuông góc với mặt phẳng đáy. Biết góc giữa và
bằng . Gọi H và K lần lượt là trung điểm của SC và SD. Thể tích của khối chóp
S.AHK là.
A..
B..
C. .
D. .
Câu 36. Cho hàm số . Tính tổng
A. .
B. .
C. .
D. .
Câu 37. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực.
A. .
B. .
C. .
D. .
Câu 38. Một ngọn hải đăng đặt ở vị trí A cách bờ biển một khoảng . Trên
bờ biển có một cái kho ở vị trí C cách B một khoảng là 7 (km). Người canh hải đăng
có thể chèo đò từ A đến vị trí M trên bờ biển với vận tốc 4 (km/h) rồi đi bộ đến C với
vận tốc 6 (km/h). Vị trí của điểm M cách B một khoảng gần nhất với giá trị nào sau
đây để người đó đến kho nhanh nhất?
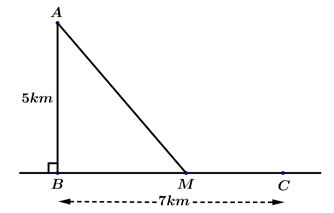
A. .
B. .
C. .
D. .
Câu 39. Một anh sinh viên được gia định gởi vào số tiết kiệm ngân hàng số tiền là
8 000 000 đồng với lãi suất 0.9%/tháng. Nếu mỗi tháng anh sinh viên đó rút ra một số
tiền như nhau vào ngày ngân hàng trã lãi thì hàng tháng anh ta rút ra bao nhiêu tiền
(làm tròn đến 1000 đồng) để sau đúng 5 năm sẽ vừa hết số tiền cả vốn lẫn lãi?
A. 180 000 đồng.
B. 171 000 đồng.
C. 173 000 đồng.
D. 175 000 đồng.
Câu 40. Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều
cao và bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O' lấy
điểm B sao cho AB = 2a. Thể tích khối tứ diện OO'AB theo a là:
A. .
B. .
C. .
D. .
PHẦN II : PHẦN TỰ LUẬN
Câu 1. Tìm m để hàm số ![]() có cực đại và cực
có cực đại và cực
tiểu với hoành độ thỏa mãn .
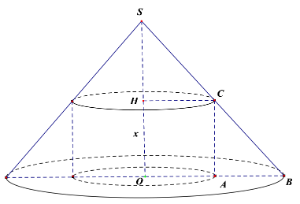
Câu 2. Một nóc nhà cao tầng có dạng một hình nón. Người ta muốn xây một bể có
dạng hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết
SO=h; OB = R và OH = x, (0<x<h) . Tìm x để hình trụ tạo ra có thể tích lớn nhất.
ĐÁP ÁN ĐỀ SỐ 1
PHẦN I: PHẦN TRẮC NGHIỆM:
Câu 1: Đáp án B
Hàm số đã cho là hàm trùng phương, có hệ số nên loại câu C và D.
Hàm số có hệ số và cùng dấu nên hàm số chỉ có một cực trị. Loại A.
Câu 2: Đáp án D
Ta thấy nên hàm số nghịch biến trên .
Câu 3: Đáp án B
Ta có là tiệm cận ngang của đồ thị hàm số.
Câu 4: Đáp án C
Điều kiện: .
Tập xác định .
Câu 5: Đáp án B
Ta có ; và đổi dấu khi qua điểm nên hàm số có 1 điểm cực trị.
Chú ý: Hàm số dạng trùng phương có các hệ số , cùng dấu nên hàm số có 1 điểm cực trị.
Câu 6: Đáp án A
Đáp án A đúng vì ta có nên .
Đáp án B sai vì .
Đáp án C sai vì .
Đáp án D sai vì .
Câu 7: Đáp án C
Lý thuyết: Đồ thị các hàm số và đối xứng nhau qua đường thẳng .
Đáp án A sai vì đồ thị các hàm số và đối xứng nhau qua trục tung.
Đáp án B sai vì đồ thị hàm số và đối xứng nhau qua trục hoành.
Câu 8: Đáp án C
Các khẳng định đúng là (I), (III), (IV).
Câu 9: Đáp án A
Câu 10: Đáp án D
Câu 11: Đáp án D
Phương trình hoành độ giao điểm của hai đồ thị là .
Suy ra hai đồ thị có ba điểm chung.
Câu 12: Đáp án B
Ta có 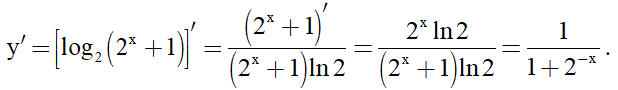
Câu 13: Đáp án B
.
.
Ta có: , . Vậy .
Câu 14: Đáp án B
Ta có
Câu 15: Đáp án D
Tập xác định: .
.
Hàm số luôn đồng biến trên .
Câu 16: Đáp án A
Để đồ thị hàm số có đúng một tiệm cận đứng thì phương trình có duy nhất nghiệm khác 1 hoặc có hai nghiệm phân biệt trong đó có một nghiêm bằng 1.
TH1:
Khi , phương trình có một nghiệm (thỏa mãn).
Khi phương trình có một nghiệm (thỏa mãn).
TH2: Phương trình có một nghiệm bằng 1 .
Thử lại, với ta có phương trình (thỏa mãn)
Vậy với , , thì đồ thị hàm số có duy nhất một tiệm cận đứng.
Câu 17: Đáp án C
hàm số nghịch biến trên [-2;0].
Câu 18: Đáp án B
Dựa vào đồ thị, ta có các nhận xét sau:
+ Ta thấy rằng .
+ Hàm số đạt cực đại tại . Ta có là nghiệm phương trình
Theo hệ thức Viét, ta có
+ Đồ thị hàm số đi qua điểm có tọa độ .
Vậy các hệ số .
Câu 19: Đáp án D
Điều kiện: .
Bất phương trình .
So với điều kiện, ta có .
Câu 20: Đáp án C
Ta có
.
Vậy .
Câu 21: Đáp án D
Hàm số có tập xác định là .
Câu 22: Đáp án C
Ta có .
Đặt . Ta có ; .
Bảng biến thiên:
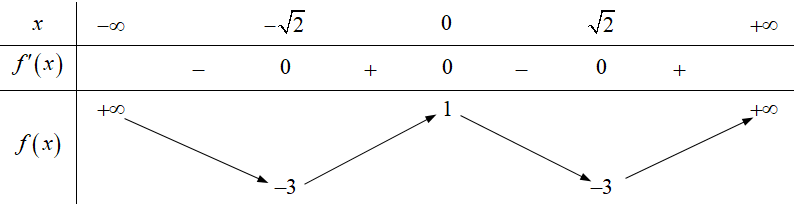
Dựa vào bảng biến thiên ta thấy phương trình có 2 nghiệm => hoặc m = -3.
Câu 23: Đáp án C
+ Các khẳng định A, B sai theo lý thuyết.
+ Xét khẳng định C: Ta có hàm số đồng biến trên C đúng.
+ Xét khẳng định D: Ta có hàm số đồng biến trên D sai.
Câu 24: Đáp án C
Ta có
.
Vì nên . Vậy có tất cả 6 nghiệm nguyên.
Câu 25: Đáp án B
Giả sử tứ diện đều .
Tính diện tích ABCD: .
Xác định chiều cao:
Gọi là chiều cao của khối chóp.
vuông tại O cho ta .
Vậy, .
Câu 26: Đáp án D
.
Câu 27: Đáp án B
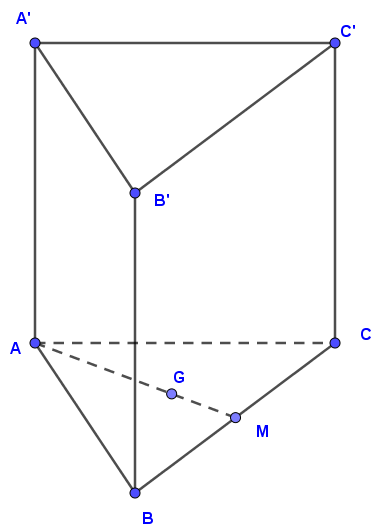
Giả sử khối lăng trụ tam giác đều là ; gọi G là trọng tâm tam giác ABC.
Gọi h là chiều cao của khối lăng trụ và x là độ dài cạnh tam giác đáy.
Do đáy là tam giác đều cạnh x nên có diện tích : .
Thể tích của khối lăng trụ tam giác đều là:
Bán kính đường tròn đáy của khối trụ ngoại tiếp là .
Thể tích khối trụ là : .
Câu 28: Đáp án A
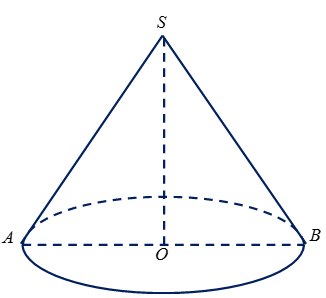
Gọi l, h, R lần lượt là độ dài đường sinh, đường cao và bán kính đáy của hình nón.
Thiết diện qua trục của hình nón là tam giác SAB vuông cân tại S có cạnh huyền .
Nên .
Ta có: .
Vậy diện tích xung quanh của hình nón: .
Câu 29: Đáp án C
Đặt cạnh lập phương là a.
Tổng diện tích các mặt lập phương là: .
Theo bài ta có: .
Vậy thể tích khối lập phương là : .
Câu 30: Đáp án B
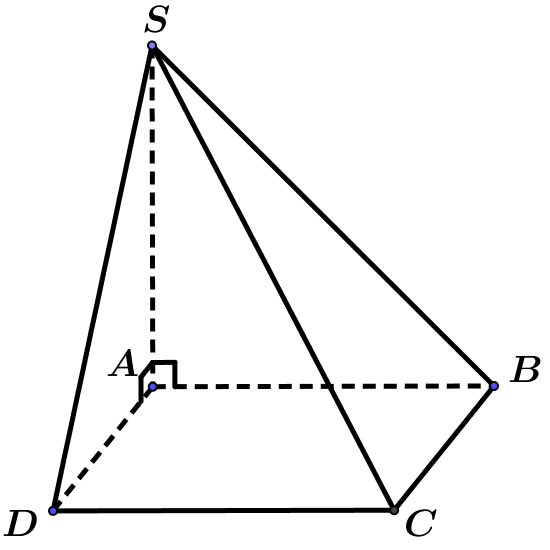
Diện tích hình chữ nhật ABCD là: .
là đường cao của chóp .
Thể tích khối chóp là: .
Câu 31: Đáp án A
Ta có .
Hàm số có hai điểm cực trị .
Khi đó hai điểm cực trị là
Vectơ chỉ phương của đường thẳng là .
Đường thẳng AB vuông góc với đường thẳng .
Vậy m = 0 hoặc m = 2.
Câu 32: Đáp án C
Điều kiện: .
Khi đó,
* TH1: : Ta có
* TH2: :
Vậy
Câu 33: Đáp án A
Ta có .
Hàm số nghịch biến trên khoảng khi .
Đồng thời .
Ta có
Vậy .
Câu 34: Đáp án B
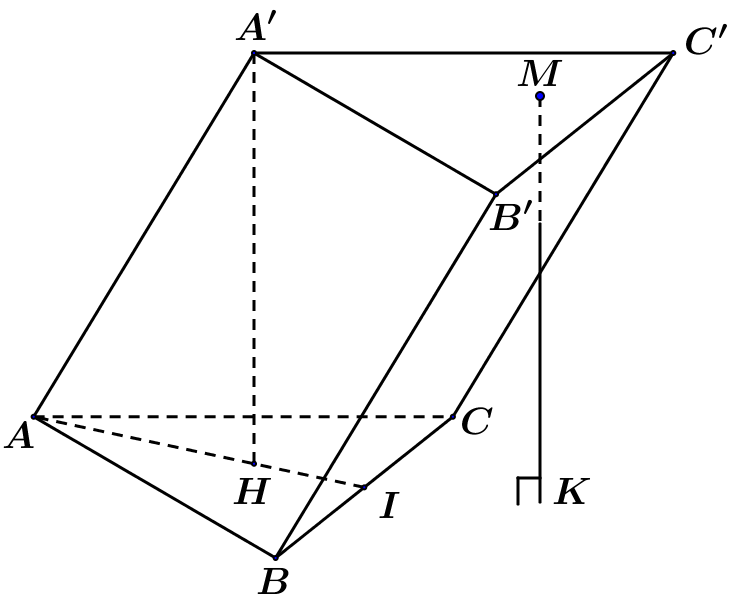
Gọi h là chiều cao của lăng trụ, . Khi đó chóp có chiều cao là h.
Thể tích lăng trụ .
Thể tích tứ diện là .
Câu 35: Đáp án A
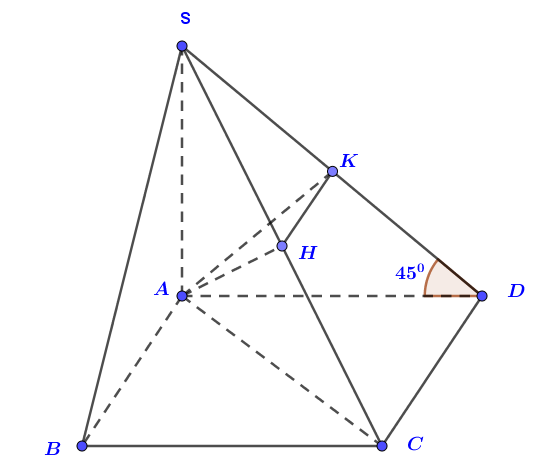
Ta có: và cùng vuông góc với mặt phẳng đáy
Câu 36: Đáp án D
Ta có .
Suy ra
Câu 37: Đáp án A
Đặt , t > 0. Ta có .
Khi đó phương trình trở thành
Xét hàm số trên khoảng , có .
Suy ra là hàm số nghịch biến trên , kết hợp với , .
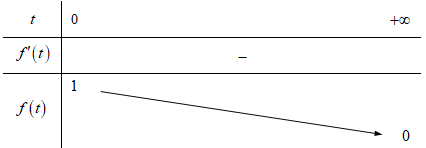
Vậy phương trình (*) có nghiệm khi và chỉ khi .
Câu 38: Đáp án C
Đặt . Khi đó .
Thời gian người canh hải đăng đi từ A đến C là (giờ)
Ta có: (km)
Hàm số F(x) đạt giá trị nhỏ nhất tại điểm do đó (km).
Câu 39: Đáp án C

Câu 40:
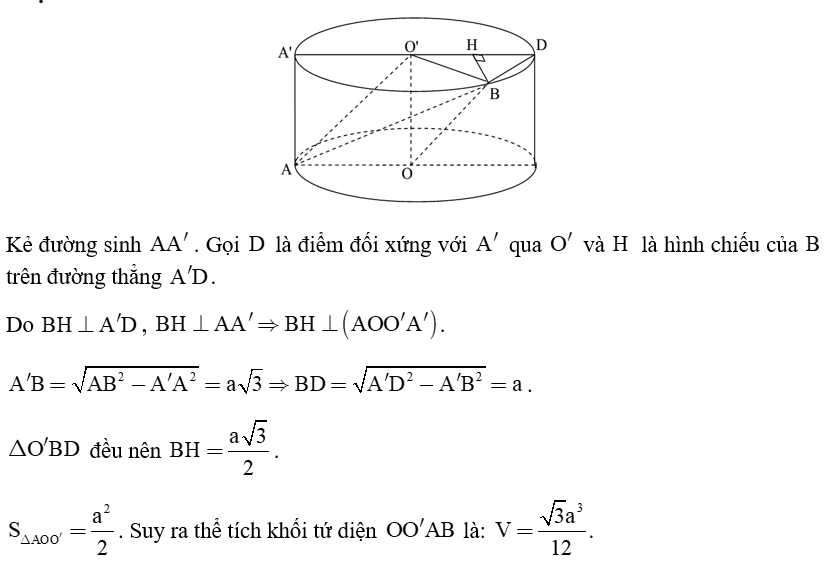
PHẦN II: PHẦN TỰ LUẬN
Câu 1:

Câu 2:

Đề thi Học kì 1 Toán lớp 12 có đáp án - đề số 2
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học ...
Môn: Toán 12
Thời gian làm bài: 90 phút
Câu 1. Cho hàm số . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số luôn nghịch biến trên từng khoảng xác định.
B. Hàm số luôn nghịch biến trên .
C. Hàm số đồng biến trên các khoảng và .
D. Hàm số nghịch biến trên các khoảng và .
Câu 2. Tìm tất cả giá trị tham số m để hàm số đồng biến trên
.
A.
B.
C. .
D. .
Câu 3. Gọi là giá trị cực đại và giá trị cực tiểu của hàm số .
Khi đó giá trị của biểu thức bằng bao nhiêu?
A. .
B. .
C. .
D. .
Câu 4. Đồ thị hàm số có điểm cực trị là .Tính giá trị của
biểu thức .
A. .
B. .
C. .
D. .
Câu 5. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
có hai điểm cực trị A,B sao cho (
trong đó O là gốc tọa độ).
A.
B. .
C. hoặc .
D. hoặc .
Câu 6. Tính tổng giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số
trên đoạn .
A. .
B. .
C. .
D. .
Câu 7. Với giá trị nào của m thì giá trị nhỏ nhất của hàm số trên đoạn bằng ?
A. .
B. .
C. .
D. .
Câu 8. Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo C và
khoảng cách ngắn nhất từ B đến C là 1km, khoảng cách từ B đến A là 4km được minh
họa bằng hình vẽ sau:
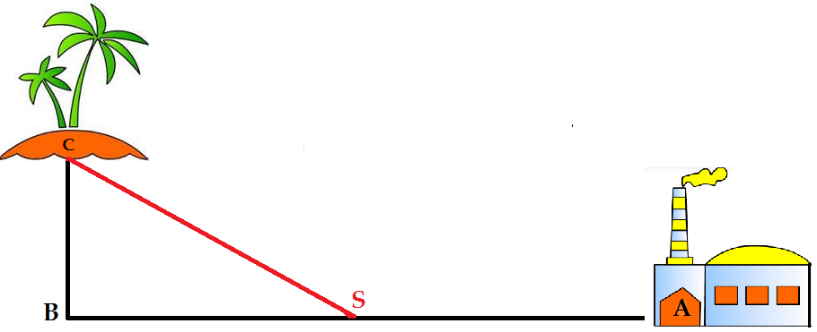
Biết rằng mỗi rằng km dây điện đặt dưới nước mất 5000 USD, còn đặt dưới đất mất
3000 USD. Hỏi điểm S trên bờ cách A bao nhiêu để khi mắc dây điện từ A qua S rồi
đến C là ít tốn kém nhất ?
A. .
B. .
C. .
D. .
Câu 9. Hàm số có đồ thị như hình vẽ. Mệnh đề nào đúng?
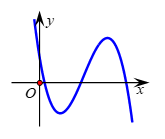
A. .
B. .
C. .
D. .
Câu 10. Số giao điểm n của hai đồ thị và là:
A. .
B. .
C. .
D. .
Câu 11. Hình vẽ bên là đồ thị hàm trùng phương. Tìm giá trị của m để phương trình
có 4 nghiệm phân biệt
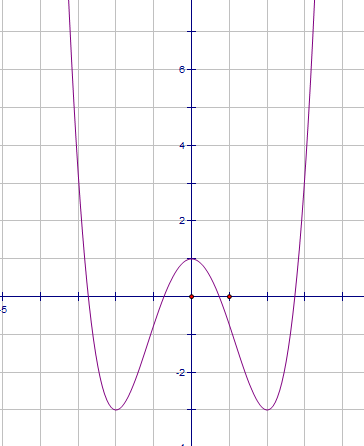
A. .
B. .
C.
D. .
Câu 12. Cho hàm số . Các giá trị của tham số m để đồ
thị hàm số (1) cắt trục hoành tại điểm phân biệt có hoành độ thoả mãn
là:
A.
B.
C.
D. .
Câu 13. Cho hàm số . Hệ số góc của tiếp tuyến với đồ thị (C) sao cho
tiếp tuyến đó cắt các trục lần lượt tại các điểm thỏa mãn là
A.
B.
C. hoặc
D. 1.
Câu 14. Cho hàm số có đồ thị (C). Có bao nhiêu điểm M thuộc (C) sao cho
khoảng cách từ điểm M đến tiệm cận ngang bằng 5 lần khoảng cách từ M đến tiệm cận
đứng.
A. 1.
B. 2.
C. 3.
D. 4.
Câu 15. Đồ thị hàm số có bao nhiêu đường tiệm cận?
A. 1.
B. 2.
C. 3.
D. 4.
Câu 16. Cho hàm số xác định trên và có đồ thị là đường cong trong hình. Mệnh đề
nào dưới đây là đúng?
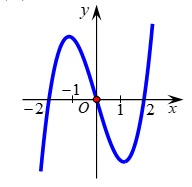
A. Hàm số nghịch biến trên khoảng .
B. Hàm số nghịch biến trên khoảng .
C. Hàm số đồng biến trên khoảng .
D. Hàm số đồng biến trên khoảng .
Câu 17. Cho biểu thức với x>0. Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Câu 18. Cho . Tìm mệnh đề đúng trong các mệnh đề sau
A. Tập giá trị của hàm số là .
B. Tập xác định của hàm số là .
C. Tập xác định của hàm số là .
D. Tập giá trị của hàm số là .
Câu 19. Nếu và thì giá trị của bằng
bao nhiêu?
A. 9.
B. 18.
C. 1.
D. 3.
Câu 20. Cho , , . Tính theo .
A. .
B. .
C. .
D. .
Câu 21. Tính đạo hàm của hàm số :
A. .
B. .
C. .
D. .
Câu 22. Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
trên đoạn . Mối liên hệ giữa m và M là:
A. .
B.
C. .
D. .
Câu 23. Trong hình vẽ dưới đây có đồ thị của các hàm số
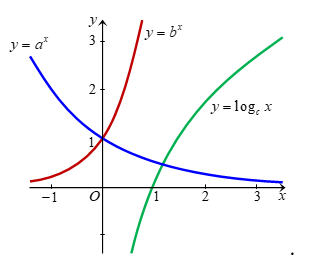
Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
A.
B.
C.
D.
Câu 24. Tính tổng T tất cả các nghiệm của phương trình trên
đoạn
A.
B.
C.
D.
Câu 25. Tập nghiệm của bất phương trình là
A.
B.
C. .
D. .
Câu 26. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm.
A. .
B. .
C. .
D. .
Câu 27. Biết phương trình có hai nghiệm . Tỉ số khi rút gọn là:
A. 4
B. .
C. 64.
D. .
Câu 28. Tổng của nghiệm nhỏ nhất và lớn nhất phương trình
bằng:
A. .
B. .
C. .
D. .
Câu 29. Khối đa diện sau có bao nhiêu mặt?
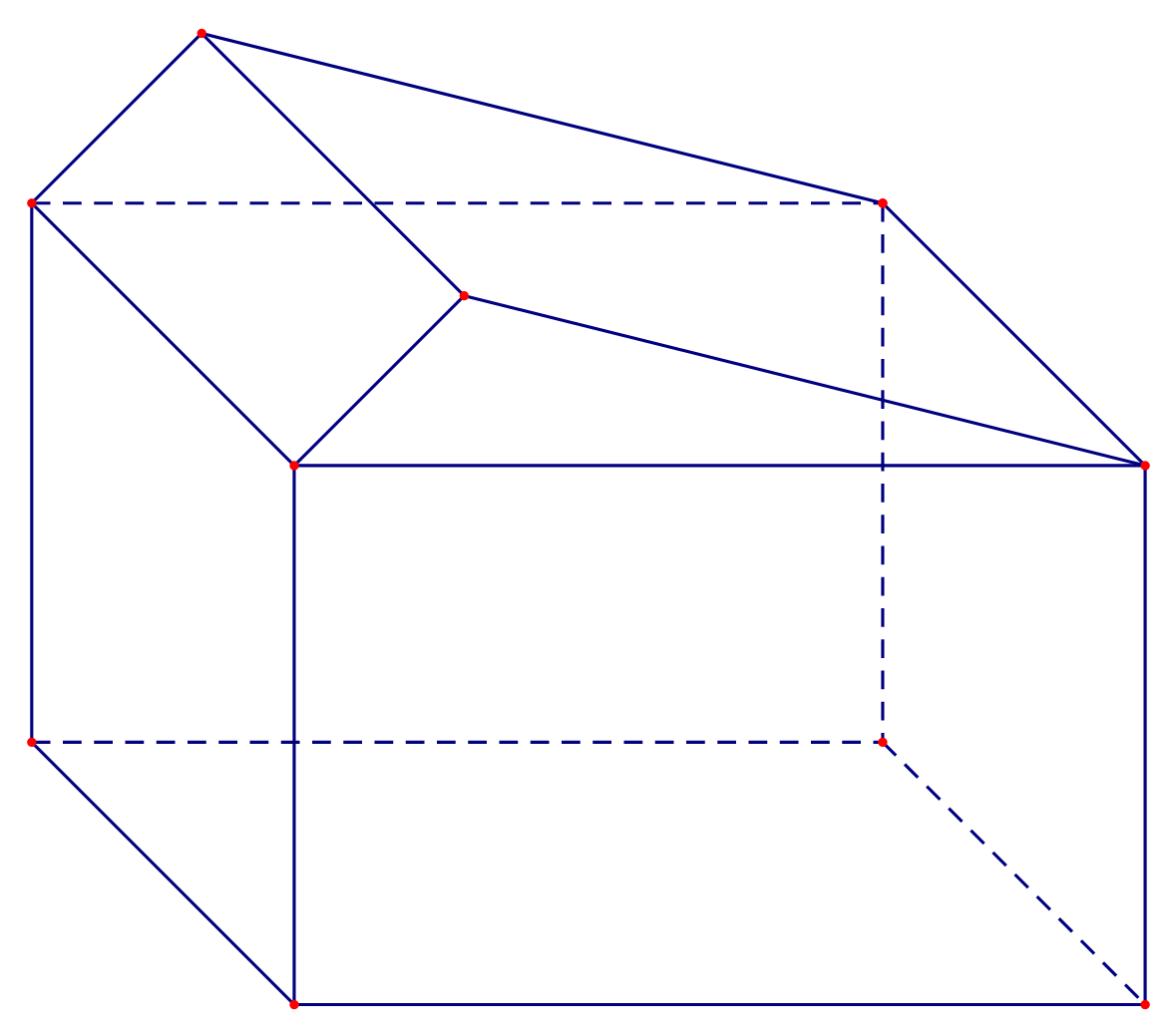
A. 9
B. 10.
C. 8.
D. 7.
Câu 30. Mặt phẳng chia khối lăng trụ thành các khối đa diện
nào ?
A. Một khối chóp tam giác và một khối chóp tứ giác.
B. Hai khối chóp tam giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác.
D. Hai khối chóp tứ giác.
Câu 31. Cho hình chóp có đáy là hình thoi cạnh a, vuông
góc với đáy, SD tạo với mặt phẳng (SAC) một góc bằng Tính thể tích V của khối
chóp S.ABCD
A.
B.
C.
D.
Câu 32. Cho hình chóp , đáy ABCD là hình vuông cạnh a. SA vuông góc
với đáy và SA=2a. Gọi M, N, P lần lượt là trung điểm của SB, SC, SD. Tính thể tích
khối đa diện AMNP.
A.
B.
C.
D.
Câu 33. Cho hình lăng trụ đều có cạnh đáy a=4 , biết diện tích tam giác
bằng 8. Tính thể tích khối lăng trụ .
A.
B. .
C. .
D. .
Câu 34. Cho lăng trụ tam giác có đáy là tam giác vuông cân tại C. Hình
chiếu vuông góc A¢ lên mặt phẳng (ABC) trùng với trung điểm cạnh AB. Biết cạnh bên
lăng trụ bằng 2a, đường cao lăng trụ bằng Tính theo a thể tích khối lăng trụ
.
A.
B.
C.
D.
Câu 35. Hình chóp tứ giác đều a có góc tạo bởi mặt bên và mặt đáy bằng M, N. Thể
tích của hình chóp là AB. Hỏi cạnh hình vuông mặt đáy bằng bao nhiêu?
A. a
B.
C.
D. 2a
Câu 36. Tính theo a thể tích V của khối hộp chữ nhật biết rằng mặt
phẳng hợp với mặt đáy một góc , hợp với đáy một
góc và .
A.
B.
C. .
D. .
Câu 37. Một hình nón có bán kính đường tròn đáy là và diện tích hình tròn đáy
bằng diện tích xung quanh của hình nón. Tính thể tích khối nón.
A. .
B. .
C.
D. .
Câu 38. Một hình nón đỉnh S tâm O có bán kính đáy bằng a góc ở đỉnh bằng .
Một mặt phẳng (P) qua đỉnh cắt đường tròn đáy tại A, B sao cho . Diện
tích thiết diện bằng:
A. .
B. .
C. .
D. .
Câu 39. Cho hình trụ (T) có chiều cao h , độ dài đường sinh l, bán kính đáy r. Ký hiệu
là diện tích xung quanh của (T). Công thức nào sau đây là đúng?
A. .
B. .
C. .
D. .
Câu 40. Cho hình nón có độ dài đường kính đáy là 2R, độ dài đường sinh là và
hình trụ có chiều cao và đường kính đáy đều bằng 2R, lồng vào nhau như hình vẽ.
Tính thể tích phần khối trụ không giao với khối nón.
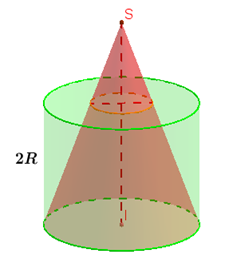
A. .
B. .
C.
D. .
PHẦN II: PHẦN TỰ LUẬN
Câu 1. Giải phương trình sau: .
Câu 2. Cho khối bát diện đều cạnh a. Tính tỷ số thể tích của khối lập phương được tạo nên bằng cách nối các tâm của các mặt bên của khối bát diện với thể tích của khối bát diện.
Đề thi Học kì 1 Toán lớp 12 có đáp án - đề số 3
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học ...
Môn: Toán 12
Thời gian làm bài: 90 phút
Câu 1: Gọi là hai số thực thoả mãn . Tổng bằng.
A. 0.
B.
C. 3.
D.
Câu 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm sô trên đoạn
lần lượt là
A. 1 và -2.
B. 0 và -2.
C. -1 và -2.
D. -1 và -3.
Câu 3: Mặt cầu qua các đỉnh của hình lập phương cạnh 2a có diện tích bằng
A.
B.
C.
D.
Câu 4: Gọi là hai số thực thoả mãn . Giá trị biểu thức
bằng
A. 36.
B. 5.
C. 20.
D. 25.
Câu 5: Hàm số có tập xác định là
A.
B.
C.
D.
Câu 6: Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h được tính bởi công
thức
A.
B.
C.
D.
Câu 7: Cho khối chóp có đôi một vuông góc với nhau và
Thể tích của khối chóp SABC bằng
A.
B.
C.
D.
Câu 8: Số giao điểm của đồ thị hàm số và đường thẳng
là
A. 0.
B. 2.
C. 3.
D. 1.
Câu 9: Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó?
A.
B.
C.
D.
Câu 10: Một miếng bìa hình tam giác đều ABC, cạnh a=16cm. Một học sinh cắt một
hình chữ nhật MNPQ từ miếng bìa trên (với M, N thuộc cạnh BC, P và Q tương ứng
thuộc cạnh AC và AB). Diện tích hình chữ nhật MNPQ lớn nhất có thể bằng
A.
B.
C.
D.
Câu 11: Đạo hàm của hàm số tại điểm x=2 bằng
A.
B.
C.
D.
Câu 12: Trong các hàm số sau, hàm số nào đồng biến trên
A.
B.
C.
D.
Câu 13: Cho bảng biến thiên như hình vẽ
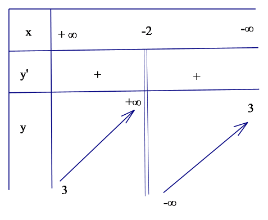
Bảng biến thiên trên là bảng biến thiên của hàm số nào trong các hàm số sau?
A.
B.
C.
D.
Câu 14: Trong các mệnh đề sau, mệnh đề nào Sai?
A. Hàm số không có cực trị.
B. Hàm số có cực trị.
C. Hàm số có hai cực trị.
D. Hàm số có cực trị.
Câu 15: Hàm số nghịch biến trên khoảng
khi và chỉ khi m thỏa mãn
A.
B.
C.
D.
Câu 16: Thể tích của khối chóp có diện tích đáy B và chiều cao h được tính bởi công
thức
A.
B.
C.
D.
Câu 17: Đạo hàm của hàm số là
A.
B.
C.
D.
Câu 18: Hàm số có hai hai cực trị . Khi đó tổng
bằng
A. 49
B. 69
C. 79
D. 39.
Câu 19: Giá trị của biểu thức bằng:
A. 3.
B. 1.
C. 5.
D. 2.
Câu 20: Các đường tiệm cận của đồ thị hàm số là
A. và
B. x=1 và
C. và
D. và
B. PHẦN CÂU HỎI TỰ LUẬN (5 điểm).
Câu 1. (2 điểm) Cho hàm số
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
b) Tìm các giá trị của tham số để phương trình sau có 3 nghiệm thực phân biệt
Câu2. (1 điểm) Cho các số thực dương thoả mãn .
a) Chứng minh rằng
b) Tìm giá trị lớn nhất của biểu thức
Câu 3. (2 điểm) Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh a, cạnh
bên SA vuông góc với mặt phẳng (ABCD) và SD= .
a) Tính thể tích khối chóp S.ABCD theo a
b) Tính bán kính mặt cầu đi qua các đỉnh của hình chóp S.ABCD.
Đề thi Học kì 1 Toán lớp 12 có đáp án - đề số 4
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học ...
Môn: Toán 12
Thời gian làm bài: 90 phút
Câu 1. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số liên tục; trục hoành và hai đường thẳng bằng
A.
B.
C.
D.
Câu 2. Nguyên hàm của hàm số là
A.
B.
C. .
D.
Câu 3. Nguyên hàm của hàm số là
A.
B.
C.
D.
Câu 4. Gọi F(x) là nguyên hàm của hàm số và . Giá trị F(3) bằng
A. ln2.
B. 2ln2 .
C. –ln2.
D. -2ln2.
Câu 5. Nguyên hàm của hàm số là
A.
B.
C.
D.
Câu 6. Giá trị của bằng
A.
B.
C.
D.
Câu 7. Diện tích hình phẳng giới hạn bởi đồ thị hàm số và đồ thị hàm số bằng
A.
B. 6.
C. 8.
D.
Câu 8. Biểu thức tích phân với m là số nguyên khác 0, là phân số tối giản. Giá trị của tổng bằng
A. S = 10.
B. S = 5.
C. S = 9.
D. S = 13.
Câu 9. Ký hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số ; trục hoành; đường thẳng x=0 và đường thẳng x=1. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox?
A.
B.
C.
D.
Câu 10. Một chiếc lò xo có độ dài tự nhiên 0,15m. Khi lò xo bị kéo giãn thêm x(m) thì xuất hiện lực đàn hồi . Tính công A của lực đàn hồi thực hiện được khi lò xo từ trạng thái có độ dài 0,18m về trạng thái tự nhiên?
A.
B.
C.
D.
Câu 11. Cho hàm số có đạo hàm trên đoạn [2; 4], , liên tục và . Giá trị bằng
A. 9.
B. 5.
C. 19.
D. 29.
Câu 12. Cho đồ thị hàm số . Diện tích hình phẳng (phần tô đậm trong hình) là
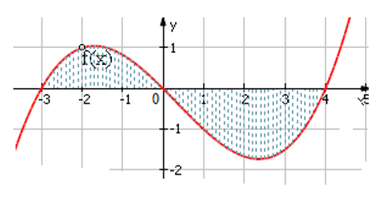
A.
B.
C.
D.
Câu 13. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số , trục tung,
trục hoành và x = 1. Tính thể tích V của khối tròn xoay thu được khi quay hình (H)
xung quanh trục Ox.
A.
B.
C.
D.
Câu 14. Biểu thức tích phân với m là số nguyên khác 0, là phân số tối giản. Giá trị của tổng bằng
A. S = 10.
B. S = 5.
C. S = 9.
D. S = 13.
Câu 15. Cho hai hàm có đạo hàm trên . Phát biểu nào sau đây
đúng ?
A. Nếu thì
B. Nếu thì
C. Nếu thì
D. Nếu thì
Câu 16. Cho hai số phức . Môđun của số phức bằng
A.
B. 17.
C. 5.
D.
Câu 17. Tìm số phức liên hợp của số phức ?
A.
B.
C.
D.
Câu 18. Cho số phức z thỏa . Môdun của số phức z bằng
A.
B.
C.
D.
Câu 19. Gọi là hai nghiệm của phương trình . Tổng bằng
A.
B.
C.
D.
Câu 20. Tọa độ điểm biểu diễn hình học của số phức z thỏa mãn là
A.
B.
C.
D.
Câu 21. Cho số phức . Số phức bằng
A.
B.
C.
D.
Câu 22. Cho số phức z thỏa mãn . Môđun số phức bằng
A. 4.
B.
C.
D. 5.
Câu 23. Gọi là nghiệm phức có phần ảo âm của phương trình . Trên
mặt phẳng tọa độ. Điểm M biểu diễn số phức có tọa độ là
A. M(-1; 2).
B. M(-1; -2).
C.
D.
Câu 24. Trong không gian với hệ toạ độ Oxyz, cho đường thẳng và mặt phẳng . Mệnh đề nào dưới đây đúng?
A. d song song với (α).
B. d nằm trong (α).
C. d vuông góc với (α).
D. d cắt (α).
Câu 25. Biết rằng nghịch đảo của số phức z bằng số phức liên hợp của nó. Trong các
kết luận sau, kết luận nào đúng?
A.
B.
C.
D.
Câu 26. Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; 1; -1) và đường thẳng
. Viết phương trình mặt phẳng qua A và vuông góc với đường
thẳng d
A. 2x - y + z = 0.
B. 2x + y + z = 0.
C. 2x - y - 1 = 0.
D. 2x - y + 1 = 0.
Câu 27. Trong không gian với hệ toạ độ Oxyz, cho vectơ . Mặt phẳng nào
có phương trình dưới đây nhận vectơ làm vectơ pháp tuyến?
A.
B. .
C.
D. .
Câu 28. Trong không gian với hệ toạ độ Oxyz, tìm toạ độ tâm I và bán kính R của mặt
cầu (S) có phương trình
A.
B. .
C. .
D.
Câu 29. Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng .
Điểm nào dưới đây có khoảng cách đến mặt phẳng (P) bằng 3?
A. (1; 1; -4).
B. (1; 1; 2).
C. (1; -1; 0).
D. (-1; 1; 6).
Câu 30. Trong không gian với hệ toạ độ Oxyz, cho 3 điểm
. Phương trình nào dưới đây là phương trình mặt phẳng
(ABC)?
A.
B.
C.
D.
Câu 31. Cho số phức thỏa mãn. . Giá trị
biểu thức bằng
A. 1.
B. 0.
C. 4.
D. 6.
Câu 32. Trong không gian với hệ toạ độ Oxyz, cho điểm A(4; -3; 1) và đường thẳng
. Viết phương trình của mặt cầu (S) đi qua điểm A có bán kính
bằng 3 và tâm của mặt cầu (S) nằm trên đường thẳng d?
A.
B.
C.
D.
Câu 33. Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; 4; -4), đường thẳng
. Viết phương trình của đường thẳng ∆ đi qua điểm A vuông góc
với d và đồng thời cắt d?
A.
B.
C.
D.
Câu 34. Trong không gian với hệ toạ độ Oxyz, cho điểm M(1; 2; 4). Viết phương trình
mặt phẳng (P) đi qua điểm M và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C
sao cho thể tích khối chóp OABC nhỏ nhất?
A.
B.
C.
D.
Câu 35. Trong không gian với hệ toạ độ Oxyz, tìm toạ độ tiếp điểm của mặt cầu (S)
và mặt phẳng (P). 2x + 3y + z – 11 = 0?
A. (3; 1; 2).
B. (-3; 1; 2).
C. (0; 0; 11).
D. (-1; 2; 15).
................................
.................................
.................................
Để xem trọn bộ Đề thi Toán 12 có đáp án, Thầy/ cô vui lòng Tải xuống!
Xem thêm các chương trình khác:
- Góp ý sgk lớp 12 tất cả các môn năm 2024 - 2025 (3 bộ sách)
- Đề thi chính thức các môn THPT Quốc Gia các năm
- (3000+) Đề thi thử THPT Quốc Gia (các năm) từ các trường, sở trên cả nước
- Đề minh họa THPT quốc gia các năm
- Đề thi Đánh giá năng lực năm 2023 | Thông tin | Cấu trúc ĐGNL ĐHQG Hà Nội, HCM, ĐHBK, Bộ Công an
