TOP 30 Đề thi Giữa học kì 2 Toán lớp 12 năm 2024 có đáp án

Chỉ từ 150k mua trọn bộ Đề thi Giữa kì 2 Toán 12 bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận đề thi.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Giữa học kì 2 Toán lớp 12 năm 2023 - 2024 có đáp án

Đề thi Giữa học kì 2 Toán lớp 12 có đáp án - đề số 1

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa học kì 2

Năm học ...

Môn: Toán 12

Thời gian làm bài: 90 phút

Câu 1: $\int \left(3{\mathrm{x}}^2+1\right)\text{\hspace{0.17em}d}\mathrm{x}$ bằng

A. $3{\mathrm{x}}^3+\mathrm{x}+\mathrm{C}$

B. ${\mathrm{x}}^3+\mathrm{x}+\mathrm{C}$

C. ${\mathrm{x}}^3+\mathrm{C}$

D. ${\frac{\mathrm{x}}{3}}^3+\mathrm{x}+\mathrm{C}$

Câu 2: Họ tất cả các nguyên hàm của hàm số f(x) = 2cosx – sinx là

A. $2\mathrm{sinx}-\mathrm{cosx}+\mathrm{C}$

B. $-2\mathrm{sinx}-\mathrm{cosx}+\mathrm{C}$

C. $2\mathrm{sinx}+\mathrm{cosx}+\mathrm{C}$

D. $-2\mathrm{sinx}+\mathrm{cosx}+\mathrm{C}$

Câu 3: $\int 2\mathrm{x}{\left({\mathrm{x}}^2+1\right)}^4\text{d}\mathrm{x}$ bằng

A. $\frac{{\left({\mathrm{x}}^2+1\right)}^5}{5}+\mathrm{C}$

B. $\frac{{\left({\mathrm{x}}^2+1\right)}^5}{4}+\mathrm{C}$

C. $\frac{2{\left({\mathrm{x}}^2+1\right)}^5}{5}+\mathrm{C}$

D. ${\left({\mathrm{x}}^2+1\right)}^5+\mathrm{C}$

Câu 4: $\int \sin \left(3\mathrm{x}-\frac{1}{3}\right)\text{\hspace{0.17em}d}\mathrm{x}$ bằng

A. $\frac{1}{3}\cos \left(3\mathrm{x}-\frac{1}{3}\right)+\mathrm{C}$

B. $-\cos \left(3\mathrm{x}-\frac{1}{3}\right)+\mathrm{C}$

C. $-\frac{1}{3}\cos \left(3\mathrm{x}-\frac{1}{3}\right)+\mathrm{C}$

D. $-\frac{1}{3}\sin \left(3\mathrm{x}-\frac{1}{3}\right)+\mathrm{C}$

Câu 5:  $\int \left(\mathrm{x}+5^{\mathrm{x}}\right)\text{\hspace{0.17em}d}\mathrm{x}$ bằng

A. $\frac{{\mathrm{x}}^2}{2}+\frac{5^{\mathrm{x}}}{\ln 5}+\mathrm{C}$

B. $\frac{{\mathrm{x}}^2}{2}+5^{\mathrm{x}}.\ln 5+\mathrm{C}$

C. $1+\frac{5^{\mathrm{x}}}{\ln 5}+\mathrm{C}$

D. ${\mathrm{x}}^2+\frac{5^{\mathrm{x}}}{\ln 5}+\mathrm{C}$

Câu 6: $\int \frac{\sqrt{1+3\mathrm{lnx}}.\mathrm{lnx}}{\mathrm{x}}\text{\hspace{0.17em}d}\mathrm{x}$ bằng

A. $\frac{2}{9}{\left(1+3\mathrm{lnx}\right)}^2\left[{\left(1+3\mathrm{lnx}\right)}^2-1\right]+\mathrm{C}$

B. $\left(1+3\mathrm{lnx}\right)\sqrt{1+3\mathrm{lnx}}\left(\frac{1+3\mathrm{lnx}}{5}-\frac{1}{3}\right)+\mathrm{C}$

C. $\frac{2}{9}\left(1+3\mathrm{lnx}\right)\sqrt{1+3\mathrm{lnx}}\left(\frac{1+3\mathrm{lnx}}{5}-\frac{1}{3}\right)+\mathrm{C}$

D. $\frac{2}{3}\left(1+3\mathrm{lnx}\right)\sqrt{1+3\mathrm{lnx}}\left(\frac{1+3\mathrm{lnx}}{5}-\frac{1}{3}\right)+\mathrm{C}$

Câu 7: Cho hàm số $\mathrm{f}\left(\mathrm{x}\right)$ thỏa mãn $\left\{\begin{array}{c}{\mathrm{e}}^{3\mathrm{x}}\left(4\mathrm{f}\left(\mathrm{x}\right)+{\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right)\right)=2\sqrt{\mathrm{f}\left(\mathrm{x}\right)}\\ \mathrm{f}\left(\mathrm{x}\right)>0\end{array}\right.,\forall \mathrm{x}\ge 0$ 

và f(0) = 1. Tính $\mathrm{I}=\underset{0}{\overset{\ln 2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}$.

A. $\mathrm{I}=\frac{1}{12}$

B. $\mathrm{I}=-\frac{1}{12}$

C. $\mathrm{I}=\frac{209}{640}$

D. $\mathrm{I}=\frac{7}{640}$

Câu 8: Biết rằng $\mathrm{g}\left(\mathrm{x}\right)$ là một nguyên hàm của $\mathrm{f}\left(\mathrm{x}\right)=(\mathrm{x}+1)\mathrm{sinx}$ và $\mathrm{g}\left(0\right)=0$, tính $\mathrm{g}\left(\mathrm{\pi }\right)$

A. 0

B. $\mathrm{\pi }+1$

C. $\mathrm{\pi }+2$

D. 1

Câu 9:  Tính $\mathrm{I}=\underset{1}{\overset{4}{\int }}\frac{\mathrm{x}+1}{2\sqrt{\mathrm{x}}}.\text{d}\mathrm{x}$

A. $\mathrm{I}=\frac{4}{3}$

B. I = 2

C. $\mathrm{I}=\frac{10}{3}$

D. $\mathrm{I}=\frac{2}{3}$

Câu 10: Cho $\underset{1}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}=3$. Khi đó $\underset{1}{\overset{2}{\int }}\frac{\mathrm{f}\left(\mathrm{x}\right)}{\text{e}}\text{\hspace{0.17em}d}\mathrm{x}$ bằng

A. $\frac{-3}{\text{e}}$

B. ${\mathrm{e}}^2$

C. $3{\mathrm{e}}^2$

D. $\frac{3}{\text{e}}$

Câu 11: $\underset{-2}{\overset{1}{\int }}\left(3{\mathrm{x}}^2-2\mathrm{x}\right)\text{\hspace{0.17em}d}\mathrm{x}$ bằng

A. 12

B. 4

C. -12

D. 8

Câu 12: $\underset{-2}{\overset{1}{\int }}\frac{2}{\mathrm{x}-2}\text{d}\mathrm{x}$ bằng

A. -2ln2

B. -4ln2

C. ln2

D. 4ln2

Câu 13: Biết rằng $\underset{0}{\overset{3}{\int }}\frac{1-{\mathrm{e}}^{3\mathrm{x}}}{{\mathrm{e}}^{2\mathrm{x}}+{\mathrm{e}}^{\mathrm{x}}+1}\hspace{0.17em}\mathrm{dx}=\mathrm{a}-{\mathrm{e}}^{\mathrm{b}}$ với $\mathrm{a},\mathrm{b}\in \mathrm{\mathbb{Z}}$, hãy tính b – a.

A. b – a = 1

B. b – a = -1

C. b – a = 7

D. b – a = -7

Câu 14: Cho hàm số y = f(x) sao cho f'(x) liên tục trên $\mathrm{ℝ}$, $\underset{1}{\overset{2}{\int }}\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{x}}\text{d}\mathrm{x}=3-\ln 2$

và f(2) = 3. Tính $\mathrm{I}=\underset{1}{\overset{2}{\int }}{\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right).\mathrm{lnx}\text{d}\mathrm{x}$.

A. I = 4ln2 – 3

B. I = 2ln2 – 3

C. I = 2ln2 + 3

D. I = 3ln2 – 4

Câu 15: Biết $\mathrm{I}=\underset{-3}{\overset{3}{\int }}\frac{\left|\mathrm{x}-2\right|-3\left|\mathrm{x}+1\right|}{\mathrm{x}+4}\text{d}\mathrm{x}=-10+\mathrm{aln}2+\mathrm{bln}3+\mathrm{cln}7$ với $\mathrm{a},\mathrm{b},\mathrm{c}\in \mathrm{\mathbb{Z}}$.

Tính T = a + b + c.

A. $\mathrm{T}=-4$

B. $\mathrm{T}=21$

C. $\mathrm{T}=9$

D. $\mathrm{T}=-12$

Câu 16: Giả sử hàm số f(x) liên tục và dương trên đoạn [0; 3] thỏa mãn $\mathrm{f}\left(\mathrm{x}\right).\mathrm{f}(3-\mathrm{x})=4$. Tính tích phân $\mathrm{I}=\underset{0}{\overset{3}{\int }}\frac{1}{2+\mathrm{f}\left(\mathrm{x}\right)}\text{d}\mathrm{x}$.

A. $\mathrm{I}=\frac{3}{5}$

B.  $\mathrm{I}=\frac{1}{2}$

C. $\mathrm{I}=\frac{3}{4}$

D. $\mathrm{I}=\frac{1}{3}$

Câu 17: Cho hàm số f(x) có đồ thị như hình vẽ bên dưới.

 

Diện tích hình phẳng giới hạn bởi đồ thị hàm số f(x) và trục Ox được tính theo công thức nào sau đây?

A. $\underset{-1}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}$

B. $\underset{\frac{1}{3}}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}$

C. $\underset{-1}{\overset{\frac{1}{3}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}-\underset{\frac{1}{3}}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}$

D. $-\underset{-1}{\overset{\frac{1}{3}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}+\underset{\frac{1}{3}}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}$

Câu 18: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}-1\right)\left(2-\mathrm{x}\right)\left({\mathrm{x}}^2+1\right)$ và trục Ox.

A. $\frac{11}{20}$

B. $\frac{1}{20}$

C. $\frac{19}{20}$

D. $\frac{117}{20}$

Câu 19: Gọi S là diện tích của hình phẳng giới hạn bởi parabol $\mathrm{y}=\frac{{\mathrm{x}}^2}{2}+\frac{3\mathrm{x}}{2}$ 

và đường thẳng y = x + 1. Ta có

A. $\mathrm{S}=\frac{3}{2}$

B. $\mathrm{S}=\frac{11}{2}$

C. $\mathrm{S}=\frac{3}{4}$

D. $\mathrm{S}=\frac{9}{4}$

Câu 20: Hình vẽ dưới đây là một mảnh vườn hình Elip có bốn đỉnh là I; J; K; L, ABCD, EFGH là các hình chữ nhật; $\mathrm{IJ}=10\hspace{0.17em}\mathrm{m},\mathrm{\hspace{0.17em}}\mathrm{KL}=\hspace{0.17em}6\hspace{0.17em}\mathrm{m}$, $\mathrm{AB}=5\hspace{0.17em}\mathrm{m},\mathrm{\hspace{0.17em}}\mathrm{EH}=3\hspace{0.17em}\mathrm{m}$. Biết rằng kinh phí trồng hoa là 50000 đồng/m², hãy tính số tiền (làm tròn đến hàng đơn vị) dùng để trồng hoa trên phần gạch sọc.

A. 2 869 834 đồng

B. 1 434 917 đồng

C. 2 119 834 đồng

D. 684 917 đồng

Câu 21: Một quần thể virut Corona P đang thay đổi với tốc độ ${\mathrm{P}}^{\text{'}}\left(\mathrm{t}\right)=\frac{5000}{1+0,2\mathrm{t}}$, trong đó t là thời gian tính bằng giờ. Quần thể virut Corona P ban đầu (khi t = 0) có số lượng là 1000 con. Số lượng virut Corona sau 3 giờ gần với số nào sau đây nhất?

A.16000

B. 21750

C. 12750

D. 11750

Câu 22: Cho hình (H) giới hạn bởi đồ thị hàm số $\mathrm{y}=\sqrt{\frac{2}{\mathrm{x}}}$, trục hoành, các đường thẳng x = 1, x = 2. Biết rằng khối tròn xoay do (H) quay quanh trục Ox tạo ra có thể tích là $\mathrm{\pi lna}$. Giá trị của a là

A. 6

B. 2

C. 4

D. 8

Câu 23: Cho hình (H) giới hạn bởi đồ thị hàm số $\mathrm{y}=\mathrm{sinx}$, $\mathrm{y}=\mathrm{cosx}$, các đường thẳng $\mathrm{x}=0,\mathrm{x}=\frac{\mathrm{\pi }}{4}$. Biết rằng khối tròn xoay do (H) quay quanh trục Ox tạo ra có thể tích là  $\frac{\mathrm{\pi }}{\mathrm{a}}$, hỏi rằng có bao nhiêu số nguyên nằm trong khoảng (a; 10)?

A. 6

B. 7

C. 8

D. 9

Câu 24: Cho hình thang cong giới hạn bởi đồ thị hàm số $\mathrm{y}=\sqrt{\mathrm{x}}$, trục hoành, các đường thẳng x = 1 và x = 4. Thể tích của khối tròn xoay được tạo thành khi quay hình thang cong trên quanh trục Ox bằng

A. $\underset{1}{\overset{4}{\int }}\sqrt{\mathrm{x}}\text{\hspace{0.17em}\hspace{0.05em}d}\mathrm{x}$

B. $\underset{1}{\overset{4}{\int }}\sqrt{\mathrm{x}}\text{\hspace{0.17em}\hspace{0.05em}d}\mathrm{x}$

C. $\mathrm{\pi }\underset{1}{\overset{4}{\int }}\sqrt{\mathrm{x}}\text{d}\mathrm{x}$

D. $\mathrm{\pi }\underset{1}{\overset{4}{\int }}{\mathrm{x}}^2\text{\hspace{0.17em}d}\mathrm{x}$

Câu 25: Cho a, b là hai số thực dương. Gọi (H) là hình phẳng giới hạn bởi parabol $\mathrm{y}={\mathrm{ax}}^2$ và đường thẳng $\mathrm{y}=-\mathrm{bx}$. Quay (H) quanh trục hoành thu được khối có thể tích là V₁, quay (H) quanh trục tung thu được khối có thể tích là V₂. Tìm b sao cho V₁ = V₂.

A. $\mathrm{b}=\frac{5}{6}$

B. $\mathrm{b}=\frac{5}{3}$

C. $\mathrm{b}=\frac{5}{2}$

D. $\mathrm{b}=\frac{5}{4}$

Câu 26:  Vận tốc (tính bằng $\frac{\mathrm{m}}{\mathrm{s}}$) của một hạt chuyển động theo một đường được xác định bởi công thức $\mathrm{v}\left(\mathrm{t}\right)={\mathrm{t}}^3-8{\mathrm{t}}^2+17\mathrm{t}-10$, trong đó t được tính bằng giây. Tổng quãng đường mà hạt đi được trong khoảng thời gian $1\le \mathrm{t}\le 5$ là bao nhiêu?

A. $\frac{32}{3}\mathrm{m}$

B. $\frac{71}{3}\mathrm{m}$

C. $\frac{38}{3}\mathrm{m}$

D. $\frac{71}{6}\mathrm{m}$

Câu 27: Biết F(x) là một nguyên hàm của hàm số $\mathrm{f}\left(\mathrm{x}\right)=4{\mathrm{x}}^3+1$ và F(0) = 1. Tính giá trị của F(1).

A. 0

B. 1

C. 2

D. 3

Câu 28: Cho hàm số f(x) xác định trên $\mathrm{ℝ}\backslash \left\{2\right\}$ thỏa mãn ${\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right)=\frac{1}{\mathrm{x}-2}$, f(1) = 2020,

f(3) = 2021. Tính P = f(4) – f(0).

A. P = 4

B. P = ln2

C. P = ln4041

D. P = 1

Câu 29: Trong không gian Oxyz, cho $\overrightarrow{\mathrm{a}}=\left(1;-2;5\right),\overrightarrow{\mathrm{b}}=\left(0;2;-1\right)$.

Nếu $\overrightarrow{\mathrm{c}}=\overrightarrow{\mathrm{a}}-4\overrightarrow{\mathrm{b}}$ thì $\overrightarrow{\mathrm{c}}$ có tọa độ là

A. $\left(1;0;4\right)$

B. $\left(1;6;1\right)$

C. $\left(1;-4;6\right)$

D. $\left(1\mathrm{\hspace{0.17em}};\mathrm{\hspace{0.17em}}-10\mathrm{\hspace{0.17em}};\mathrm{\hspace{0.17em}}9\right)$

Câu 30: Trong không gian Oxyz, cho hai điểm $\mathrm{A}\left(-2;1;1\right)$, $\mathrm{B}\left(3;2;-1\right)$.

Độ dài đoạn thẳng AB bằng

A. $\sqrt{30}$

B. $\sqrt{10}$

C. $\sqrt{22}$

D. 2

Câu 31: Trong không gian Oxyz, cho $\overrightarrow{\mathrm{u}}=\left(2;-3;4\right)$, $\overrightarrow{\mathrm{v}}=\left(-3;-2;2\right)$ 

khi đó $\overrightarrow{\mathrm{u}}.\overrightarrow{\mathrm{v}}$ bằng

A. 20

B. 8

C. $\sqrt{46}$

D. $2\sqrt{2}$

Câu 32: Trong không gian Oxyz, cho $\mathrm{A}\left(1;0;6\right)$, $\mathrm{B}\left(0;2;-1\right)$, $\mathrm{C}\left(1;4;0\right)$. Bán kính mặt cầu (S) có tâm $\mathrm{I}\left(2;2;-1\right)$ và tiếp xúc với mặt phẳng (ABC) bằng

A. $\frac{8\sqrt{3}}{3}$

B. $\frac{8\sqrt{77}}{77}$

C. $\frac{16\sqrt{77}}{77}$

D. $\frac{16\sqrt{3}}{3}$

Câu 33: Trong không gian Oxyz, cho mặt cầu $\left(\mathrm{S}\right):{\left(\mathrm{x}+1\right)}^2+{\left(\mathrm{y}-2\right)}^2+{\left(\mathrm{z}-1\right)}^2=4$.

Tìm tọa độ tâm I và bán kính R của mặt cầu (S).

A. $\mathrm{I}\left(-1;2;1\right)$ và $\mathrm{R}=2$

B. $\mathrm{I}\left(1;-2;-1\right)$ và $\mathrm{R}=2$

C. $\mathrm{I}\left(-1;2;1\right)$ và $\mathrm{R}=4$

D. $\mathrm{I}\left(1;-2;-1\right)$ và $\mathrm{R}=4$

Câu 34: Trong không gian Oxyz cho hai điểm $\mathrm{A}(-2;1;0)$, $\mathrm{B}(2;-1;2)$.

Phương trình mặt cầu (S) có tâm B và đi qua A là

A. ${\left(\mathrm{x}-2\right)}^2+{\left(\mathrm{y}+1\right)}^2+{(\mathrm{z}-2)}^2=\sqrt{24}$

B. ${\left(\mathrm{x}-2\right)}^2+{\left(\mathrm{y}+1\right)}^2+{(\mathrm{z}-2)}^2=24$

C. ${\left(\mathrm{x}+2\right)}^2+{\left(\mathrm{y}-1\right)}^2+{\mathrm{z}}^2=24$

D. ${\left(\mathrm{x}-2\right)}^2+{\left(\mathrm{y}-1\right)}^2+{(\mathrm{z}-2)}^2=24$

Câu 35: Trong không gian Oxyz cho hai điểm $\mathrm{A}(-2;1;0)$, $\mathrm{B}(2;-1;4)$.

Phương trình mặt cầu (S) có đường kính AB là

A. ${\mathrm{x}}^2+{\mathrm{y}}^2+{(\mathrm{z}-2)}^2=3$

B. ${\mathrm{x}}^2+{\mathrm{y}}^2+{(\mathrm{z}+2)}^2=3$

C. ${\mathrm{x}}^2+{\mathrm{y}}^2+{(\mathrm{z}-2)}^2=9$

D. ${\mathrm{x}}^2+{\mathrm{y}}^2+{(\mathrm{z}+2)}^2=9$

Câu 36: Thể tích khối cầu ngoại tiếp tứ diện đều ABCD cạnh a là

A. $\mathrm{V}=\frac{{\mathrm{\pi a}}^3\sqrt{6}}{8}$

B. $\mathrm{V}=\frac{{\mathrm{\pi a}}^3\sqrt{6}}{4}$

C. $\mathrm{V}=\frac{{\mathrm{\pi a}}^3\sqrt{3}}{8}$

D. $\mathrm{V}=\frac{{\mathrm{\pi a}}^2\sqrt{6}}{8}$

Câu 37: Trong không gian Oxyz, cho mặt cầu (S) có tâm thuộc trục Ox và đi qua hai điểm $\mathrm{A}\left(1;2;-1\right)$ và $\mathrm{B}\left(2;1;3\right)$. Phương trình của (S) là

A. ${\left(\mathrm{x}-4\right)}^2+{\mathrm{y}}^2+{\mathrm{z}}^2=14$

B. ${\left(\mathrm{x}+4\right)}^2+{\mathrm{y}}^2+{\mathrm{z}}^2=14$

C. ${\mathrm{x}}^2+{(\mathrm{y}-4)}^2+{\mathrm{z}}^2=14$

D. ${\mathrm{x}}^2+{\mathrm{y}}^2+{(\mathrm{z}-4)}^2=14$

Câu 38:  Trong không gian Oxyz, cho mặt cầu (S) có tâm $\mathrm{I}\left(1;-2;3\right)$ và tiếp xúc với mặt phẳng $\left(\mathrm{P}\right):2\mathrm{x}-2\mathrm{y}+\mathrm{z}+3=0$. Phương trình của (S) là

A. ${\left(\mathrm{x}-1\right)}^2+{\left(\mathrm{y}+2\right)}^2+{\left(\mathrm{z}-3\right)}^2=16$

B. ${\left(\mathrm{x}-1\right)}^2+{\left(\mathrm{y}+2\right)}^2+{\left(\mathrm{z}-3\right)}^2=9$

C. ${\left(\mathrm{x}+1\right)}^2+{\left(\mathrm{y}-2\right)}^2+{\left(\mathrm{z}+3\right)}^2=16$

D. ${\left(\mathrm{x}-1\right)}^2+{\left(\mathrm{y}+2\right)}^2+{\left(\mathrm{z}-3\right)}^2=4$

Câu 39: Trong không gian Oxyz cho $\mathrm{A}\left(\mathrm{a};0;0\right)$, $\mathrm{B}\left(0;\mathrm{b};0\right)$, $\mathrm{C}\left(0;0;\mathrm{c}\right)$, $\mathrm{D}\left(\mathrm{a}+\mathrm{a}\sqrt{{\mathrm{b}}^2+{\mathrm{c}}^2};\mathrm{b}\sqrt{{\mathrm{a}}^2+{\mathrm{c}}^2};\mathrm{c}\sqrt{{\mathrm{a}}^2+{\mathrm{b}}^2}\right)$ ($\mathrm{a}>0$, $\mathrm{b}>0$, $\mathrm{c}>0$). Diện tích tam giác ABC bằng $\frac{\sqrt{3}}{2}$. Tìm khoảng cách từ B đến mặt phẳng (ACD) khi ${\mathrm{V}}_{\mathrm{A}.\mathrm{BCD}}$ đạt giá trị lớn nhất.

A. $\frac{\sqrt{6}}{2}$

B. $\sqrt{3}$

C. $\sqrt{2}$

D. $\frac{\sqrt{2}}{2}$

Câu 40: Trong không gian với hệ tọa độ Oxyz, cho hai điểm $\mathrm{E}\left(1;1;3\right);\mathrm{F}(0;1;0)$ và mặt phẳng $\left(\mathrm{P}\right):\mathrm{x}+\mathrm{y}+\mathrm{z}-1=0.$ Gọi $\mathrm{M}(\mathrm{a};\mathrm{b};\mathrm{c})\in \left(\mathrm{P}\right)$ sao cho $\left|2\overrightarrow{\mathrm{ME}}-3\overrightarrow{\mathrm{MF}}\right|$ đạt giá trị nhỏ nhất. Tính $\mathrm{T}=3\text{a}+2\mathrm{b}+\mathrm{c}.$

A. 4

B. 3

C. 6

D. 1

Câu 41: Trong không gian Oxyz, cho hai điểm $\mathrm{A}(1;2;5),\mathrm{B}(3;0;-1)$. Mặt phẳng trung trực của đoạn thẳng AB có phương trình là

A. $\mathrm{x}+\mathrm{y}-3\mathrm{z}+6=0$

B. $\mathrm{x}-\mathrm{y}-3\mathrm{z}+5=0$

C. $\mathrm{x}-\mathrm{y}-3\mathrm{z}+1=0$

D. $2\mathrm{x}+\mathrm{y}+2\mathrm{z}+10=0$

Câu 42: Trong không gian Oxyz, mặt phẳng đi qua điểm $\mathrm{A}\left(-1;2;4\right)$ và song song với mặt phẳng $\left(\mathrm{P}\right):4\mathrm{x}+\mathrm{y}-\mathrm{z}+5=0$ có phương trình là

A. $4\mathrm{x}+\mathrm{y}+\mathrm{z}-5=0$

B. $4\mathrm{x}+\mathrm{y}+\mathrm{z}-2=0$

C. $4\mathrm{x}+\mathrm{y}-\mathrm{z}=0$

D. $4\mathrm{x}+\mathrm{y}-\mathrm{z}+6=0$

Câu 43: Trong không gian Oxyz, gọi (P) là mặt phẳng đi qua điểm $\mathrm{M}\left(-4;1;2\right)$, đồng thời vuông góc với hai mặt phẳng $\left(\mathrm{Q}\right):\mathrm{x}-3\mathrm{y}+\mathrm{z}-4=0$ và $\left(\mathrm{R}\right):2\mathrm{x}-\mathrm{y}+3\mathrm{z}+1=0$. Phương trình của (P) là

A. $8\mathrm{x}-\mathrm{y}+5\mathrm{z}+23=0$

B. $4\mathrm{x}+\mathrm{y}-5\mathrm{z}+25=0$

C. $8\mathrm{x}+\mathrm{y}-5\mathrm{z}+41=0$

D. $8\mathrm{x}-\mathrm{y}-5\mathrm{z}-43=0$

Câu 44: Trong không gian Oxyz, cho mặt cầu (S):${\left(\mathrm{x}+1\right)}^2+{\left(\mathrm{y}-2\right)}^2+{\left(\mathrm{z}-1\right)}^2=9$. Mặt phẳng (P) tiếp xúc với (S) tại điểm $\mathrm{A}\left(1;3;-1\right)$ có phương trình là

A. $2\mathrm{x}+\mathrm{y}-2\mathrm{z}-7=0$

B. $2\mathrm{x}+\mathrm{y}+2\mathrm{z}-7=0$

C. $2\mathrm{x}-\mathrm{y}+\mathrm{z}+10=0$

D. $2\mathrm{x}+\mathrm{y}-2\mathrm{z}+2=0$

Câu 45: Trong không gian Oxyz, cho mặt phẳng $\left(\mathrm{P}\right):2\mathrm{x}-\mathrm{y}+2\mathrm{z}+1=0$ và hai điểm $\mathrm{A}\left(1;0;-2\right), \mathrm{B}\left(-1;-1;3\right)$. Mặt  phẳng (Q) đi qua hai điểm A, B và vuông góc với (P) có phương trình dạng $\mathrm{ax}-\mathrm{by}+\mathrm{cz}+5=0$. Khẳng định nào sau đây đúng?

A. $\mathrm{a}+\mathrm{b}+\mathrm{c}=21$

B. $\mathrm{a}+\mathrm{b}+\mathrm{c}=\text{\hspace{0.17em}7}$

C. $\mathrm{a}+\mathrm{b}+\mathrm{c}=\text{\hspace{0.17em}-}21$

D. $\mathrm{a}+\mathrm{b}+\mathrm{c}=\text{\hspace{0.17em}-7}$

Câu 46: Trong không gian Oxyz, cho ba điểm$\mathrm{A}\left(0;1;2\right), \mathrm{B}\left(2;-2;1\right)$, $\mathrm{C}\left(-2;1;0\right)$. Khi đó mặt phẳng (ABC) có phương trình là

A. $\mathrm{x}+\mathrm{y}-\mathrm{z}+1=0$

B. $6\mathrm{x}+\mathrm{y}-\mathrm{z}-6=0$

C. $\mathrm{x}-\mathrm{y}+\mathrm{z}+6=0$

D. $\mathrm{x}+\mathrm{y}-\mathrm{z}-3=0$

Câu 47: Trong không gian Oxyz, cho mặt phẳng (Q) song song mặt phẳng $\left(\mathrm{P}\right):2\mathrm{x}-2\mathrm{y}+\mathrm{z}+17=0$. Biết mặt phẳng (P) cắt mặt cầu $\left(\mathrm{S}\right):{\mathrm{x}}^2+{\left(\mathrm{y}-2\right)}^2+{\left(\mathrm{z}+1\right)}^2=25$ theo giao tuyến là một đường tròn có bán kính r = 3. Khi đó mặt phẳng (Q) có phương trình là

A. $2\mathrm{x}-2\mathrm{y}+\mathrm{z}-7=0$

B. $2\mathrm{x}-2\mathrm{y}+\mathrm{z}-17=0$

C. $2\mathrm{x}-2\mathrm{y}+\mathrm{z}+17=0$

D. $\mathrm{x}-\mathrm{y}+2\mathrm{z}-7=0$

Câu 48: Trong không gian Oxyz, mặt phẳng $\left(\mathrm{\alpha }\right):\mathrm{y}=0$ trùng với mặt phẳng nào dưới đây ?

A. $\left(\mathrm{Oxy}\right)$

B. $\left(\mathrm{Oyz}\right)$

C. $\left(\mathrm{Oxz}\right)$

D. x - y = 0

Câu 49: Trong không gian Oxyz, cho bốn điểm $\mathrm{A}\left(1;0;0\right)$, $\mathrm{B}\left(0;2;0\right)$, $\mathrm{C}\left(0;0;4\right)$, $\mathrm{M}\left(0;0;3\right)$. Tính khoảng cách từ M đến mặt phẳng (ABC).

A. $\frac{4\sqrt{21}}{21}$

B. $\frac{2}{21}$

C. $\frac{1}{21}$

D. $\frac{3\sqrt{21}}{21}$

Câu 50: Trong không gian Oxyz, cho mặt phẳng (P): z = 0 và hai điểm $\mathrm{A}\left(2;-1;0\right)$, $\mathrm{B}\left(4;3;-2\right)$. Gọi $\mathrm{M}\left(\mathrm{a};\mathrm{b};\mathrm{c}\right)\in \left(\mathrm{P}\right)$ sao cho MA = Mb và góc $\widehat{\mathrm{AMB}}$ có số đo lớn nhất. Khi đó đẳng thức nào sau đây đúng?

A. $\mathrm{c}>0$

B. $\mathrm{a}+2\mathrm{b}=-6$

C. $\mathrm{a}+\mathrm{b}=0$

D. $\mathrm{a}+\mathrm{b}=\frac{23}{5}$

 

I. BẢNG ĐÁP ÁN

 

II. ĐÁP ÁN CHI TIẾT

Câu 1: Đáp án B.

Lời giải

Ta có: $\int \left(3{\mathrm{x}}^2+1\right)\text{\hspace{0.17em}d}\mathrm{x}=3\frac{{\mathrm{x}}^3}{3}+\mathrm{x}+\mathrm{C}={\mathrm{x}}^3+\mathrm{x}+\mathrm{C}$.

Câu 2: Đáp án C.

Lời giải

Ta có: $\int \left(2\mathrm{cosx}-\mathrm{sinx}\right)\text{\hspace{0.17em}d}\mathrm{x}=2\mathrm{sinx}+\mathrm{cosx}+\mathrm{C}$.

Câu 3: Đáp án A.

Lời giải

Đặt $\mathrm{t}={\mathrm{x}}^2+1$, ta được $\text{d}\mathrm{t}\text{=2}\mathrm{x}\text{d}\mathrm{x}$.

Khi đó $\int 2\mathrm{x}{\left({\mathrm{x}}^2+1\right)}^4\text{d}\mathrm{x}$$=\int {\mathrm{t}}^4\text{d}\mathrm{t}=\frac{{\mathrm{t}}^5}{5}+\mathrm{C}$.

Thay $\mathrm{t}={\mathrm{x}}^2+1$, ta được $\int 2\mathrm{x}{\left({\mathrm{x}}^2+1\right)}^4\text{d}\mathrm{x}$$=\frac{{\left({\mathrm{x}}^2+1\right)}^5}{5}+\mathrm{C}$.

Câu 4: Đáp án C.

Lời giải

Ta có: $\int \sin \left(3\mathrm{x}-\frac{1}{3}\right)\text{d}\mathrm{x}=-\frac{1}{3}\cos \left(3\mathrm{x}-\frac{1}{3}\right)+\mathrm{C}$.

Câu 5: Đáp án A.

Lời giải

Ta có  $\int \mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}=\int \left(\mathrm{x}+5^{\mathrm{x}}\right)\text{\hspace{0.17em}d}\mathrm{x}=\frac{{\mathrm{x}}^2}{2}+\frac{5^{\mathrm{x}}}{\ln 5}+\mathrm{C}$

Câu 6: Đáp án C.

Lời giải

Đặt $\mathrm{t}=\sqrt{1+3\mathrm{lnx}}$, suy ra ${\mathrm{t}}^2=1+3\mathrm{lnx}$.

Ta có: $2\mathrm{t}\text{d}\mathrm{t}=\frac{3}{\mathrm{x}}\text{d}\mathrm{x}$; $\mathrm{lnx}=\frac{{\mathrm{t}}^2-1}{3}$.

Khi đó:

$$\begin{gathered} \int \frac{\sqrt{1+3\mathrm{lnx}}.\mathrm{lnx}}{\mathrm{x}}\text{\hspace{0.17em}d}\mathrm{x}=\int \mathrm{t}\cdot \frac{{\mathrm{t}}^2-1}{3}\cdot \frac{2}{3}\cdot \mathrm{t}\text{d}\mathrm{t} \\ =\frac{2}{9}\int \left({\mathrm{t}}^4-{\mathrm{t}}^2\right)\text{\hspace{0.17em}d}\mathrm{t}=\frac{2}{9}\left(\frac{{\mathrm{t}}^5}{5}-\frac{{\mathrm{t}}^3}{3}\right)+\mathrm{C} \end{gathered}$$

Hay:

$$\begin{gathered} \int \frac{\sqrt{1+3\mathrm{lnx}}.\mathrm{lnx}}{\mathrm{x}}\text{\hspace{0.17em}d}\mathrm{x} \\ =\frac{2}{9}\left(1+3\mathrm{lnx}\right)\sqrt{1+3\mathrm{lnx}}\left(\frac{1+3\mathrm{lnx}}{5}-\frac{1}{3}\right)+\mathrm{C} \end{gathered}$$

Câu 7: Đáp án C.

Lời giải

Ta có:

${\text{e}}^{3\mathrm{x}}\left(4\mathrm{f}\left(\mathrm{x}\right)+{\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right)\right)=2\sqrt{\mathrm{f}\left(\mathrm{x}\right)}\iff 2{\text{e}}^{2\mathrm{x}}\sqrt{\mathrm{f}\left(\mathrm{x}\right)}+{\text{e}}^{2\mathrm{x}}.\frac{{\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right)}{2\sqrt{\mathrm{f}\left(\mathrm{x}\right)}}=\frac{1}{{\text{e}}^{\mathrm{x}}}$

$\iff {\left({\text{e}}^{2\mathrm{x}}.\sqrt{\mathrm{f}\left(\mathrm{x}\right)}\right)}^{\text{'}}=\frac{1}{{\text{e}}^{\mathrm{x}}}$

Do đó:

${\text{e}}^{2\mathrm{x}}.\sqrt{\mathrm{f}\left(\mathrm{x}\right)}$ là một nguyên hàm của $\frac{1}{{\text{e}}^{\mathrm{x}}}$, tức ${\text{e}}^{2\mathrm{x}}.\sqrt{\mathrm{f}\left(\mathrm{x}\right)}$$=-\frac{1}{{\text{e}}^{\mathrm{x}}}+\mathrm{C}$

Thay $\mathrm{x}=0$ vào ta được $\mathrm{C}=2$. Tìm được $\mathrm{f}\left(\mathrm{x}\right)={\left(\frac{2}{{\text{e}}^{2\mathrm{x}}}-\frac{1}{{\text{e}}^{3\mathrm{x}}}\right)}^2$

  $$\begin{gathered} \mathrm{I}=\underset{0}{\overset{\ln 2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}=\underset{0}{\overset{\ln 2}{\int }}{\left(\frac{2}{{\text{e}}^{2\mathrm{x}}}-\frac{1}{{\text{e}}^{3\mathrm{x}}}\right)}^2\text{d}\mathrm{x} \\ =\underset{0}{\overset{\ln 2}{\int }}\left(\frac{4}{{\text{e}}^{4\mathrm{x}}}-\frac{4}{{\text{e}}^{5\mathrm{x}}}+\frac{1}{{\text{e}}^{6\mathrm{x}}}\right)\text{d}\mathrm{x}=\frac{209}{640} \end{gathered}$$

Câu 8: Đáp án C.

Lời giải

Ta có:

$$\begin{gathered} \int \left(\mathrm{x}+1\right)\mathrm{sinx}\text{d}\mathrm{x}=\int \left(\mathrm{x}+1\right){\left(-\mathrm{cosx}\right)}^{\text{'}}\text{d}\mathrm{x} \\ =-(\mathrm{x}+1)\mathrm{cosx}+\int \cos \mathrm{x}\text{\hspace{0.17em}d}\mathrm{x} \end{gathered}$$

$=-(\mathrm{x}+1)\mathrm{cosx}+\mathrm{sinx}+\mathrm{C}$

Lúc này:

Xét $\mathrm{g}\left(\mathrm{x}\right)=-(\mathrm{x}+1)\mathrm{cosx}+\mathrm{sinx}+\mathrm{C}$ với $\mathrm{g}\left(0\right)=0$ ta có $\mathrm{C}=1$

Tức $\mathrm{g}\left(\mathrm{x}\right)=-(\mathrm{x}+1)\mathrm{cosx}+\mathrm{sinx}+1$.

Vậy $\mathrm{g}\left(\mathrm{\pi }\right)=\mathrm{\pi }+2$.

Câu 9:  Đáp án C.

Lời giải

$$\begin{gathered} \mathrm{I}=\underset{1}{\overset{4}{\int }}\frac{\mathrm{x}+1}{2\sqrt{\mathrm{x}}}.\text{d}\mathrm{x}\text{=}\underset{1}{\overset{4}{\int }}\left(\frac{\sqrt{\mathrm{x}}}{2}-\frac{1}{2\sqrt{\mathrm{x}}}\right).\text{d}\mathrm{x} \\ \text{=}{\left.\left(\frac{1}{3}\sqrt{{\mathrm{x}}^3}-\sqrt{\mathrm{x}}\right)\right|}_1^4=\frac{10}{3} \end{gathered}$$.

Câu 10: Đáp án D.

Lời giải

Ta có $\underset{1}{\overset{2}{\int }}\frac{\mathrm{f}\left(\mathrm{x}\right)}{\text{e}}\text{\hspace{0.17em}d}\mathrm{x}=\frac{1}{\text{e}}\underset{1}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}=\frac{3}{\text{e}}$.

Câu 11: Đáp án A.

Lời giải

Ta có: $\underset{-2}{\overset{1}{\int }}\left(3{\mathrm{x}}^2-2\mathrm{x}\right)\text{\hspace{0.17em}d}\mathrm{x}={\left.\left({\mathrm{x}}^3-{\mathrm{x}}^2\right)\right|}_{-2}^1=12$.

Câu 12: Đáp án B.

Lời giải

Ta có:

$\underset{-2}{\overset{1}{\int }}\frac{2}{\mathrm{x}-2}\text{d}\mathrm{x}=2\underset{-2}{\overset{1}{\int }}\frac{1}{\mathrm{x}-2}\text{d}\mathrm{x}={\left.2\ln \left|\mathrm{x}-2\right|\right|}_{-2}^1=-4\ln 2$.

Câu 13: Đáp án B.

Lời giải

Ta có:

$$\begin{gathered} \underset{0}{\overset{3}{\int }}\frac{1-{\mathrm{e}}^{3\mathrm{x}}}{{\mathrm{e}}^{2\mathrm{x}}+{\mathrm{e}}^{\mathrm{x}}+1}\hspace{0.17em}\mathrm{dx}=\underset{0}{\overset{3}{\int }}\frac{\left(1-{\mathrm{e}}^{\mathrm{x}}\right)\left({\mathrm{e}}^{2\mathrm{x}}+{\mathrm{e}}^{\mathrm{x}}+1\right)}{{\mathrm{e}}^{2\mathrm{x}}+{\mathrm{e}}^{\mathrm{x}}+1}\hspace{0.17em}\mathrm{dx} \\ =\underset{0}{\overset{3}{\int }}\left(1-{\mathrm{e}}^{\mathrm{x}}\right)\mathrm{dx} ={\left.\left(\mathrm{x}-{\mathrm{e}}^{\mathrm{x}}\right)\right|}_0^3=4-{\mathrm{e}}^3 \end{gathered}$$

Suy ra $\mathrm{a}=4;\mathrm{b}=3$.

Câu 14: Đáp án A.

Lời giải

Đặt $\left\{\begin{array}{l}\mathrm{u}=\mathrm{lnx}\\ \text{d}\mathrm{v}={\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right)\text{d}\mathrm{x}\end{array}\right.$, chọn $\left\{\begin{array}{l}\text{d}\mathrm{u}=\frac{1}{\mathrm{x}}\text{d}\mathrm{x}\\ \mathrm{v}=\mathrm{f}\left(\mathrm{x}\right)\end{array}\right.$.

Ta có:

$$\begin{gathered} \mathrm{I}={\left.\left[\mathrm{f}\left(\mathrm{x}\right).\mathrm{lnx}\right]\right|}_1^2-\underset{1}{\overset{2}{\int }}\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{x}}\text{d}\mathrm{x}=\mathrm{f}\left(2\right).\ln 2-3+\ln 2 \\ =4\ln 2-3 \end{gathered}$$.

Câu 15: Đáp án C.

Lời giải

Đặt $\mathrm{f}\left(\mathrm{x}\right)=\left|\mathrm{x}-2\right|-3\left|\mathrm{x}+1\right|$.

Ta có bảng phá dấu trị tuyệt đối trong biểu thức $\mathrm{f}\left(\mathrm{x}\right)$như sau

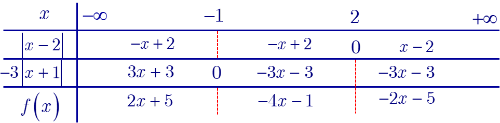
Từ đó:

$\mathrm{I}=\underset{-3}{\overset{-1}{\int }}\frac{2\mathrm{x}+5}{\mathrm{x}+4}\text{d}\mathrm{x}+\underset{-1}{\overset{2}{\int }}\frac{-4\mathrm{x}-1}{\mathrm{x}+4}\text{d}\mathrm{x}+\underset{2}{\overset{3}{\int }}\frac{-2\mathrm{x}-5}{\mathrm{x}+4}\text{d}\mathrm{x}$

$\mathrm{I}=\underset{-3}{\overset{-1}{\int }}\left(2-\frac{3}{\mathrm{x}+4}\right)\text{d}\mathrm{x}-\underset{-1}{\overset{2}{\int }}\left(4-\frac{15}{\mathrm{x}+4}\right)\text{d}\mathrm{x}-\underset{2}{\overset{3}{\int }}\left(2-\frac{3}{\mathrm{x}+4}\right)\text{d}\mathrm{x}$

$\mathrm{I}=-10-6\ln 3+12\ln 2+3\ln 7$.

Vậy ta có $\mathrm{a}=12,\mathrm{b}=-6,\mathrm{c}=3\Rightarrow \mathrm{T}=9$.

Câu 16: Đáp án C.

Lời giải

Ta có $\left\{\begin{array}{l}\mathrm{f}\left(\mathrm{x}\right).\mathrm{f}\left(3-\mathrm{x}\right)=4\\ \mathrm{f}\left(\mathrm{x}\right)>0,\forall \mathrm{x}\in \left[0;3\right]\end{array}\right.\Rightarrow \mathrm{f}\left(3-\mathrm{x}\right)=\frac{4}{\mathrm{f}\left(\mathrm{x}\right)}$.

$\mathrm{I}=\underset{0}{\overset{3}{\int }}\frac{1}{2+\mathrm{f}\left(\mathrm{x}\right)}\text{\hspace{0.17em}d}\mathrm{x}$

Đặt $\mathrm{t}=3-\mathrm{x}\Rightarrow \text{d}\mathrm{t}=-\text{d}\mathrm{x}$

Đổi cận $\mathrm{x}=0\Rightarrow \mathrm{t}=3;\mathrm{x}=3\Rightarrow \mathrm{t}=0$.

Thay vào ta được:

 $\mathrm{I}=\underset{0}{\overset{3}{\int }}\frac{1}{2+\mathrm{f}\left(3-\mathrm{t}\right)}\mathrm{dt}$$=\underset{0}{\overset{3}{\int }}\frac{1}{2+\mathrm{f}\left(3-\mathrm{x}\right)}\text{\hspace{0.17em}d}\mathrm{x}=\underset{0}{\overset{3}{\int }}\frac{1}{2+\frac{4}{\mathrm{f}\left(\mathrm{x}\right)}}\text{\hspace{0.17em}d}\mathrm{x}$

$=\underset{0}{\overset{3}{\int }}\frac{\mathrm{f}\left(\mathrm{x}\right)}{2\mathrm{f}\left(\mathrm{x}\right)+4}\text{\hspace{0.17em}d}\mathrm{x}=\frac{1}{2}\underset{0}{\overset{3}{\int }}\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{f}\left(\mathrm{x}\right)+2}\text{\hspace{0.17em}d}\mathrm{x}$

$$\begin{gathered} =\frac{1}{2}\underset{0}{\overset{3}{\int }}\frac{\mathrm{f}\left(\mathrm{x}\right)+2-2}{\mathrm{f}\left(\mathrm{x}\right)+2}\text{\hspace{0.17em}d}\mathrm{x}=\frac{1}{2}\underset{0}{\overset{3}{\int }}\left(1-\frac{2}{\mathrm{f}\left(\mathrm{x}\right)+2}\right)\text{\hspace{0.17em}d}\mathrm{x} \\ =\frac{1}{2}{\left.\mathrm{x}\right|}_0^3-\underset{0}{\overset{3}{\int }}\frac{1}{\mathrm{f}\left(\mathrm{x}\right)+2}\text{\hspace{0.17em}d}\mathrm{x}=\frac{3}{2}-\mathrm{I} \end{gathered}$$

$\Rightarrow \mathrm{I}=\frac{3}{2}-\mathrm{I}\Rightarrow 2\mathrm{I}=\frac{3}{2}\Rightarrow \mathrm{I}=\frac{3}{4}$.

Vậy $\mathrm{I}=\frac{3}{4}$.

Câu 17: Đáp án D.

Lời giải

Diện tích hình phẳng giới hạn bởi đồ thị hàm số $\mathrm{f}\left(\mathrm{x}\right)$ và trục Ox được tính theo công thức $\underset{-1}{\overset{2}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)\right|\text{d}\mathrm{x}=-\underset{-1}{\overset{\frac{1}{3}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}+\underset{\frac{1}{3}}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}$.

Câu 18: Đáp án A.

Lời giải

Phương trình hoành độ giao điểm của đồ thị hàm số f (x) và trục Ox là:

$\left(\mathrm{x}-1\right)\left(2-\mathrm{x}\right)\left({\mathrm{x}}^2+1\right)=0$.

Phương trình nêu trên có tập nghiệm là $\left\{1;2\right\}$ và $\mathrm{f}\left(\mathrm{x}\right)\ge 0,\forall \mathrm{x}\in \left[1;2\right]$.

Do đó, diện tích mà ta cần tính là

$\mathrm{S}=\underset{1}{\overset{2}{\int }}\left|\left(\mathrm{x}-1\right)\left(2-\mathrm{x}\right)\left({\mathrm{x}}^2+1\right)\right|\text{\hspace{0.17em}d}\mathrm{x}$

$=\underset{1}{\overset{2}{\int }}\left[\left(\mathrm{x}-1\right)\left(2-\mathrm{x}\right)\left({\mathrm{x}}^2+1\right)\right]\text{\hspace{0.17em}d}\mathrm{x}=\frac{11}{20}$.

Câu 19: Đáp án D.

Lời giải

Phương trình hoành độ giao điểm của hai đường đã cho là

$\begin{array}{l}\frac{{\mathrm{x}}^2}{2}+\frac{3\mathrm{x}}{2}=\mathrm{x}+1\\ \iff \frac{{\mathrm{x}}^2}{2}+\frac{\mathrm{x}}{2}-1=0\\ \iff \left[\begin{array}{c}\mathrm{x}=-2\\ \mathrm{x}=1\end{array}.\right.\end{array}$

Cách 1. (Dựa vào đồ thị)

Ta có:

$$\begin{gathered} \mathrm{S}=\underset{-2}{\overset{1}{\int }}\left(\mathrm{x}+1-\frac{{\mathrm{x}}^2}{2}-\frac{3\mathrm{x}}{2}\right)\text{d}\mathrm{x}=\underset{-2}{\overset{1}{\int }}\left(-\frac{{\mathrm{x}}^2}{2}-\frac{\mathrm{x}}{2}+1\right)\text{d}\mathrm{x} \\ =\left.\left(-\frac{{\mathrm{x}}^3}{6}-\frac{{\mathrm{x}}^2}{4}+\mathrm{x}\right)\right|\begin{array}{c}1\\ -2\end{array}=\frac{9}{4}. \end{gathered}$$

Cách 2. (Không vẽ đồ thị)

Ta có:

$$\begin{gathered} \mathrm{S}=\left|\underset{-2}{\overset{1}{\int }}\left(\frac{{\mathrm{x}}^2}{2}+\frac{3\mathrm{x}}{2}-\mathrm{x}-1\right)\text{d}\mathrm{x}\right|=\left|\underset{-2}{\overset{1}{\int }}\left(\frac{{\mathrm{x}}^2}{2}+\frac{\mathrm{x}}{2}-1\right)\text{d}\mathrm{x}\right| \\ =\left|\left.\left(\frac{{\mathrm{x}}^3}{6}+\frac{{\mathrm{x}}^2}{4}-\mathrm{x}\right)\right|\begin{array}{c}1\\ -2\end{array}\right|=\left|-\frac{9}{4}\right|=\frac{9}{4}. \end{gathered}$$

Câu 20: Đáp án C.

Lời giải

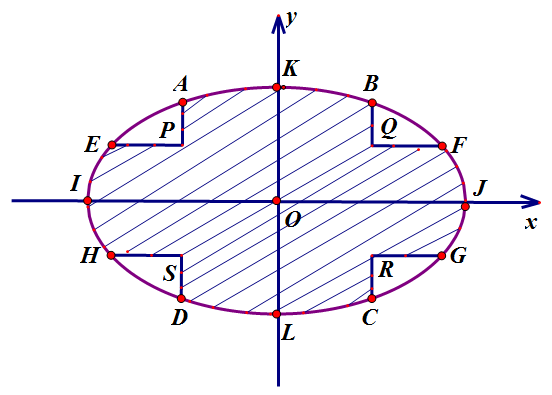
Gọi Elip đã cho là ( E ).

Dựng hệ trục Oxy như hình vẽ, khi đó ( E ) có phương trình là:

 $\frac{{\mathrm{x}}^2}{25}+\frac{{\mathrm{y}}^2}{9}=1.$

Suy ra:

+ Phần phía trên trục $\mathrm{Ox}$ của $\left(\mathrm{E}\right)$ có phương trình là:

 $\mathrm{y}=\frac{3}{5}\sqrt{25-{\mathrm{x}}^2}$.

+ Phần phía bên phải trục $\mathrm{Oy}$ của ( E ) có phương trình là:

 $\mathrm{x}=\frac{5}{3}\sqrt{9-{\mathrm{y}}^2}.$

Diện tích hình phẳng giới hạn bởi $\left(\mathrm{E}\right),\mathrm{AD},\mathrm{BC}$ là:

$$\begin{gathered} {\mathrm{S}}_1=4\underset{0}{\overset{2,5}{\int }}\frac{3}{5}\sqrt{25-{\mathrm{x}}^2}\text{d}\mathrm{x} \\ =\frac{12}{5}\left(\frac{25\mathrm{\pi }}{12}+\frac{25\sqrt{3}}{8}\right)=\left(5\mathrm{\pi }+\frac{15\sqrt{3}}{2}\right){\text{\hspace{0.17em}m}}^{\text{2}}. \end{gathered}$$

Diện tích hình phẳng giới hạn bởi $\left(\mathrm{E}\right),\mathrm{EF},\mathrm{GH}$ là:

$$\begin{gathered} {\mathrm{S}}_2=4\underset{0}{\overset{1,5}{\int }}\frac{5}{3}\sqrt{9-{\mathrm{y}}^2}\text{dy} \\ =\frac{20}{3}\left(\frac{9\mathrm{\pi }}{12}+\frac{9\sqrt{3}}{8}\right)=\left(5\mathrm{\pi }+\frac{15\sqrt{3}}{2}\right){\text{\hspace{0.17em}m}}^{\text{2}}. \end{gathered}$$

Diện tích phần đất trồng hoa (phần gạch sọc) là:

$\mathrm{S}={\mathrm{S}}_1+{\mathrm{S}}_2-{\mathrm{S}}_{\mathrm{PQRS}}=2.\left(5\mathrm{\pi }+\frac{15\sqrt{3}}{2}\right)-15{\text{\hspace{0.17em}m}}^{\text{2}}.$

Vậy số tiền dùng để trồng hoa là : S.50000 đồng, làm tròn đến hàng đơn vị là  2119834 đồng.

Câu 21: Đáp án C.

Lời giải

Ta có:

$$\begin{gathered} \mathrm{P}\left(\mathrm{t}\right)=\int {\mathrm{P}}^{\text{'}}\left(\mathrm{t}\right)\text{d}\mathrm{t}=\int \frac{5000}{1+0,2\mathrm{t}}\text{d}\mathrm{t} \\ =5000.\frac{1}{0,2}\ln \left(1+0,2\mathrm{t}\right)+\mathrm{C} \\ =25000.\ln \left(1+0,2\mathrm{t}\right)+\mathrm{C} \end{gathered}$$

$\mathrm{P}\left(0\right)=1000$$\iff \mathrm{C}=1000$.

Vậy biểu thức tính số lượng virut Corona với thời gian t bất kỳ là:

$\mathrm{P}\left(\mathrm{t}\right)=25000.\ln \left(1+0,2\mathrm{t}\right)+1000$.

Với t = 3 giờ ta có:

$\mathrm{P}\left(3\right)=25000.\ln \left(1+0,2.3\right)+1000\approx 12750,09$.

Vậy số lượng virut khi t = 3 giờ khoảng $12750$ con.

Câu 22: Đáp án C.

Lời giải

Thể tích khối tròn xoay nêu trên là: $\mathrm{V}=\mathrm{\pi }\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}{\mathrm{f}}^2\left(\mathrm{x}\right)\text{d}\mathrm{x}=\mathrm{\pi }\underset{1}{\overset{2}{\int }}\frac{2}{\mathrm{x}}\text{d}\mathrm{x}=2\mathrm{\pi }{\left.\mathrm{lnx}\right|}_1^2=2\mathrm{\pi ln}2=\mathrm{\pi ln}4$.

Vậy a = 4.

Câu 23: Đáp án B.

Lời giải

Do trên đoạn $\left[0;\frac{\mathrm{\pi }}{4}\right]$ ta có $\mathrm{cosx}\ge \mathrm{sinx}$ nên thể tích của khối đã nêu là:

$$\begin{gathered} \mathrm{V}=\mathrm{\pi }\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}{\cos }^2\mathrm{x}\text{d}\mathrm{x}-\mathrm{\pi }\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}{\sin }^2\mathrm{x}\text{d}\mathrm{x} \\ =\mathrm{\pi }\underset{0}{\overset{\frac{\mathrm{\pi }}{4}}{\int }}\text{cos2}\mathrm{x}\text{d}\mathrm{x}=\frac{\mathrm{\pi }}{2}{\left.\sin 2\mathrm{x}\right|}_0^{\frac{\mathrm{\pi }}{4}}=\frac{\mathrm{\pi }}{2} \end{gathered}$$

Trong khoảng $\left(2;10\right)$ có 7 số nguyên.

Câu 24: Đáp án B.

Lời giải

Công thức tính thể tích khối tròn xoay quay quanh trục Ox là:

$\mathrm{V}=\mathrm{\pi }\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}{\mathrm{f}}^2\left(\mathrm{x}\right)\text{\hspace{0.17em}d}\mathrm{x}=\mathrm{\pi }\underset{1}{\overset{4}{\int }}\mathrm{x}\text{\hspace{0.17em}d}\mathrm{x}$.

Câu 25: Đáp án D.

Lời giải

                                

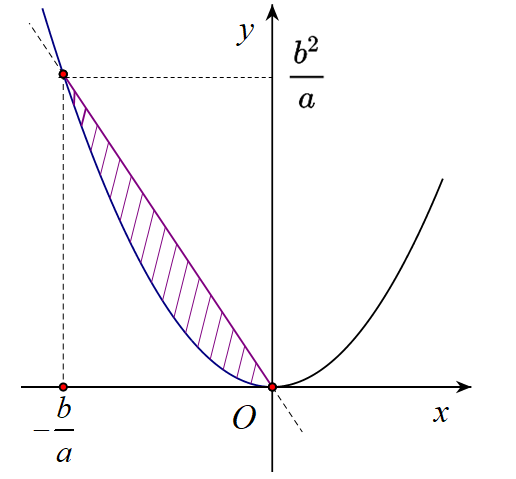
Phương trình hoành độ giao điểm của parabol và đường thẳng đã cho là:

${\mathrm{ax}}^2=-\mathrm{bx}$.

Do: ${\mathrm{ax}}^2=-\mathrm{bx}$$\iff$$\left[\begin{array}{l}\mathrm{x}=0\\ \mathrm{x}=-\frac{\mathrm{b}}{\mathrm{a}}\end{array}\right.{\mathrm{ax}}^2=-\mathrm{bx}$ 

nên các giao điểm là O và $\mathrm{M}\left(-\frac{\mathrm{b}}{\mathrm{a}};\frac{{\mathrm{b}}^2}{\mathrm{a}}\right)$ (Tham khảo hình vẽ kèm theo)

Đến đây ta có:

+ ${\mathrm{V}}_1=\mathrm{\pi }\underset{-\frac{\mathrm{b}}{\mathrm{a}}}{\overset{0}{\int }}{\left(-\mathrm{bx}\right)}^2\text{d}\mathrm{x}$$-\mathrm{\pi }\underset{-\frac{\mathrm{b}}{\mathrm{a}}}{\overset{0}{\int }}{\left({\mathrm{ax}}^2\right)}^2\text{d}\mathrm{x}$

$={\mathrm{\pi b}}^2.{\left.\frac{{\mathrm{x}}^3}{3}\right|}_{-\frac{\mathrm{b}}{\mathrm{a}}}^0-{\mathrm{\pi a}}^2.{\left.\frac{{\mathrm{x}}^5}{5}\right|}_{-\frac{\mathrm{b}}{\mathrm{a}}}^0$$=\frac{2{\mathrm{\pi b}}^5}{15{\mathrm{a}}^3}$ (đơn vị thể tích).

+  ${\mathrm{V}}_2=\mathrm{\pi }\underset{0}{\overset{\frac{{\mathrm{b}}^2}{\mathrm{a}}}{\int }}{\left(-\sqrt{\frac{\mathrm{y}}{\mathrm{a}}}\right)}^2\text{d}\mathrm{y}-\mathrm{\pi }\underset{0}{\overset{\frac{{\mathrm{b}}^2}{\mathrm{a}}}{\int }}{\left(-\frac{\mathrm{y}}{\mathrm{b}}\right)}^2\text{d}\mathrm{y}$

$=\mathrm{\pi }{\left.\frac{{\mathrm{y}}^2}{2\mathrm{a}}\right|}_0^{\frac{{\mathrm{b}}^2}{\mathrm{a}}}-\mathrm{\pi }{\left.\frac{{\mathrm{y}}^3}{3{\mathrm{b}}^2}\right|}_0^{\frac{{\mathrm{b}}^2}{\mathrm{a}}}$$=\frac{{\mathrm{\pi b}}^4}{6{\mathrm{a}}^3}$ (đơn vị thể tích)

Do vậy ${\mathrm{V}}_1={\mathrm{V}}_2$$\iff \frac{2{\mathrm{\pi b}}^5}{15{\mathrm{a}}^3}=\frac{{\mathrm{\pi b}}^4}{6{\mathrm{a}}^3}\iff \mathrm{b}=\frac{5}{4}.$

Câu 26: Đáp án D.

Lời giải

Tổng quãng đường mà hạt đi được trong khoảng thời gian $1\le \mathrm{t}\le 5$ là:

$$\begin{gathered} \underset{1}{\overset{5}{\int }}\left|\mathrm{v}\left(\mathrm{t}\right)\right|\text{d}\mathrm{t}=\underset{1}{\overset{5}{\int }}\left|{\mathrm{t}}^3-8{\mathrm{t}}^2+17\mathrm{t}-10\right|\text{d}\mathrm{t} \\ =\underset{1}{\overset{2}{\int }}\left|{\mathrm{t}}^3-8{\mathrm{t}}^2+17\mathrm{t}-10\right|\text{d}\mathrm{t}+\underset{2}{\overset{5}{\int }}\left|{\mathrm{t}}^3-8{\mathrm{t}}^2+17\mathrm{t}-10\right|\text{d}\mathrm{t} \end{gathered}$$

$=\underset{1}{\overset{2}{\int }}\left({\mathrm{t}}^3-8{\mathrm{t}}^2+17\mathrm{t}-10\right)\text{d}\mathrm{t}+\underset{2}{\overset{5}{\int }}-\left({\mathrm{t}}^3-8{\mathrm{t}}^2+17\mathrm{t}-10\right)\text{d}\mathrm{t}$

$=\left(\frac{1}{4}{\mathrm{t}}^4-\frac{8}{3}{\mathrm{t}}^3+\frac{17}{2}{\mathrm{t}}^2-10\mathrm{t}\right)\left|\begin{array}{l}2\\ 1\end{array}\right.-\left(\frac{1}{4}{\mathrm{t}}^4-\frac{8}{3}{\mathrm{t}}^3+\frac{17}{2}{\mathrm{t}}^2-10\mathrm{t}\right)\left|\begin{array}{l}5\\ 2\end{array}\right.$

 $=\frac{71}{6}$(m).

Câu 27: Đáp án D.

Lời giải

Ta có: $\int \mathrm{f}\left(\mathrm{x}\right)\text{d}\mathrm{x}=\int \left(4{\mathrm{x}}^3+1\right)\text{d}\mathrm{x}={\mathrm{x}}^4+\mathrm{x}+\mathrm{C}$.

Xét $\mathrm{F}\left(\mathrm{x}\right)={\mathrm{x}}^4+\mathrm{x}+\mathrm{C}$ với $\mathrm{F}\left(0\right)=1$ ta tìm được:

C = 1, tức $\mathrm{F}\left(\mathrm{x}\right)={\mathrm{x}}^4+\mathrm{x}+1$.

Vậy $\mathrm{F}\left(1\right)=3$.

Câu 28: Đáp án D.

Lời giải

Ta có:

$$\begin{gathered} \int {\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right)\text{d}\mathrm{x}=\int \frac{1}{\mathrm{x}-2}\text{d}\mathrm{x}=\ln \left|\mathrm{x}-2\right|+\mathrm{C} \\ =\left\{\begin{array}{l}\ln \left(\mathrm{x}-2\right)+{\mathrm{C}}_1\mathrm{khi}\mathrm{x}>2\\ \ln \left(2-\mathrm{x}\right)+{\mathrm{C}}_2\mathrm{khi}\mathrm{x}<2\end{array}\right. \end{gathered}$$

Theo giả thiết: $\mathrm{f}\left(1\right)=2020$, $\mathrm{f}\left(3\right)=2021$

$\Rightarrow \left\{\begin{array}{l}\ln 1+{\mathrm{C}}_1=2021\\ \ln 1+{\mathrm{C}}_2=2020\end{array}\right.\Rightarrow \left\{\begin{array}{l}{\mathrm{C}}_1=2021\\ {\mathrm{C}}_2=2020\end{array}\right.$

$\Rightarrow \mathrm{f}\left(\mathrm{x}\right)=\left\{\begin{array}{l}\ln \left(\mathrm{x}-2\right)+2021\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}khi\hspace{0.17em}}\mathrm{x}>2\\ \ln \left(2-\mathrm{x}\right)+2020\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}khi\hspace{0.17em}}\mathrm{x}<2\end{array}\right.$.

Do đó $\mathrm{P}=\mathrm{f}\left(4\right)-\mathrm{f}\left(0\right)$ $=\ln 2+2021-\ln 2-2020=1$.

Câu 29: Đáp án D.

Lời giải

Ta có: $\overrightarrow{\mathrm{a}}=\left(1;-2;5\right)$; $4\overrightarrow{\mathrm{b}}=\left(0;8;-4\right)$.

Vậy tọa độ của vectơ $\overrightarrow{\mathrm{c}}=\overrightarrow{\mathrm{a}}-4\overrightarrow{\mathrm{b}}$$=\left(1;-10;9\right)$.

Câu 30: Đáp án A.

Lời giải

Ta có: $\overrightarrow{\mathrm{AB}}=\left(5;1;-2\right)$.

$\text{AB\hspace{0.17em}=}\left|\overrightarrow{AB}\right|=\sqrt{5^2+1^2+{\left(-2\right)}^2}=\sqrt{30}$.

Câu 31: Đáp án B.

Lời giải

Ta có: $\overrightarrow{\mathrm{u}}.\overrightarrow{\mathrm{v}}=2.\left(-3\right)+\left(-3\right).\left(-2\right)+4.2=8$.

Câu 32: Đáp án C.

Lời giải

Ta có:

$\overrightarrow{\mathrm{AB}}=\left(-1;2;-7\right)$, $\overrightarrow{\mathrm{AC}}=\left(0;4;-6\right)$ nên $\left[\overrightarrow{\mathrm{AB}},\overrightarrow{\mathrm{AC}}\right]=\left(16;-6;-4\right)$.

$\left[\overrightarrow{\mathrm{AB}},\overrightarrow{\mathrm{AC}}\right]$ là vectơ pháp tuyến của $\left(\mathrm{ABC}\right)$,  vì thế  $\overrightarrow{\mathrm{n}}=\left(8;-3;-2\right)$ cũng  là vectơ pháp tuyến của $\left(\mathrm{ABC}\right)$.

Phương trình của mặt phẳng (ABC) là:

$8\left(\mathrm{x}-1\right)-3\mathrm{y}-2\left(\mathrm{z}-6\right)=0\iff 8\mathrm{x}-3\mathrm{y}-2\mathrm{z}+4=0$.

Gọi r là bán kính của ( S ), ta có ( S ) tiếp xúc với $\left(\mathrm{ABC}\right)$

$\iff$$\mathrm{r}=\mathrm{d}\left(\mathrm{I},\left(\mathrm{ABC}\right)\right)$.

Vậy $\mathrm{r}=\frac{\left|8.\left(2\right)-3.\left(2\right)-2.\left(-1\right)+4\right|}{\sqrt{8^2+{\left(-3\right)}^2+{\left(-2\right)}^2}}=\frac{16\sqrt{77}}{77}$.

Câu 33: Đáp án A.

Lời giải

Dựa vào phương trình của ( S ) ta thấy tọa độ tâm $\mathrm{I}\left(-1;2;1\right)$ và R = 2.

Câu 34: Đáp án B.

Lời giải

Ta có: $\overrightarrow{\mathrm{AB}}=(4;-2;2)$ nên$\mathrm{AB}=\sqrt{24}$.

Vì ( S ) có tâm B và đi qua điểm A nên bán kính của ( S ) là R = AB.

Do đó ( S ) có phương trình là ${\left(\mathrm{x}-2\right)}^2+{\left(\mathrm{y}+1\right)}^2+{(\mathrm{z}-2)}^2=24$.

Câu 35: Đáp án C.

Lời giải

Do (S) có đường kính AB nên nó nhận trung điểm I của AB làm tâm và $\frac{\mathrm{AB}}{2}$ làm bán kính.

Ta có:

+ $\overrightarrow{\mathrm{AB}}=(4;-2;4)$$\Rightarrow \mathrm{AB}=6$.

+ $\mathrm{I}(0;0;2)$.

Vậy ( S ) có phương trình là ${\mathrm{x}}^2+{\mathrm{y}}^2+{(\mathrm{z}-2)}^2=9$.

Câu 36: Đáp án A.

Lời giải

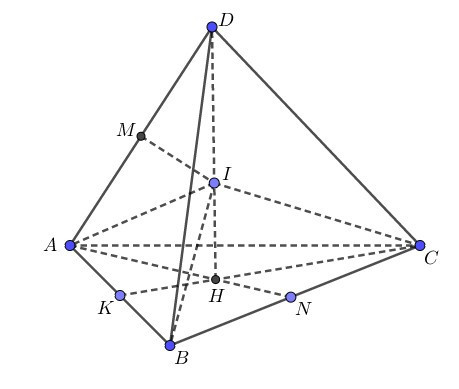
Gọi H là tâm đường tròn ngoại tiếp $\mathrm{\Delta ABC}$.

Vì ABCD là tứ diện đều nên DH là trục của đường tròn ngoại tiếp $\mathrm{\Delta ABC}$.

Mặt phẳng trung trực của cạnh AD cắt DH tại I suy ra ID là bán kính của mặt cầu ngoại tiếp tứ diện ABCD.

Gọi M là trung điểm cạnh AD ta có  $\mathrm{\Delta DMI}\backsim \mathrm{\Delta DHA}$

$\Rightarrow \frac{\mathrm{DM}}{\mathrm{DH}}=\frac{\mathrm{DI}}{\mathrm{DA}}$.

$$\begin{gathered} \Rightarrow \mathrm{ID}=\frac{{\mathrm{DA}}^2}{2\mathrm{DH}}=\frac{{\mathrm{AD}}^2}{2.\sqrt{{\mathrm{AD}}^2-{\mathrm{AH}}^2}} \\ =\frac{{\mathrm{a}}^2}{2\sqrt{{\mathrm{a}}^2-{\left(\frac{\mathrm{a}}{\sqrt{3}}\right)}^2}}=\frac{\mathrm{a}\sqrt{6}}{4} \end{gathered}$$

Vậy thể tích của khối cầu ngoại tiếp tứ diện ABCD là: $\mathrm{V}=\frac{4}{3}\mathrm{\pi }.{\mathrm{ID}}^3=\frac{4}{3}\mathrm{\pi }.{\left(\frac{\mathrm{a}\sqrt{6}}{4}\right)}^3=\frac{{\mathrm{\pi a}}^3\sqrt{6}}{8}.$

Câu 37: Đáp án A.

Lời giải

Gọi $\mathrm{I}\left(\mathrm{a};0;0\right)$ thuộc trục Ox là tâm của (S).

Ta có:

$$\begin{gathered} \mathrm{IA}=\mathrm{IB}\iff {\mathrm{IA}}^2={\mathrm{IB}}^2 \\ \iff {\left(1-\mathrm{a}\right)}^2+2^2+{(-1)}^2={(2-\mathrm{a})}^2+1^2+3^2 \\ \iff \mathrm{a}=4. \end{gathered}$$

Suy ra I(4; 0; 0) và IA² = 14.

Vậy phương trình của (S) là:

${\left(\mathrm{x}-4\right)}^2+{\mathrm{y}}^2+{\mathrm{z}}^2=14.$

Câu 38: Đáp án A.

Lời giải

Ta có $\mathrm{d}\left(\mathrm{I},\left(\mathrm{P}\right)\right)=\frac{\left|2.1-2.(-2)+3+3\right|}{\sqrt{2^2+{(-2)}^2+1^2}}=\frac{12}{3}=4$.

(S) tiếp xúc với (P)$\iff \mathrm{d}\left(\mathrm{I},\left(\mathrm{P}\right)\right)$ bằng bán kính của (S).

Vậy phương trình của (S) là ${\left(\mathrm{x}-1\right)}^2+{\left(\mathrm{y}+2\right)}^2+{\left(\mathrm{z}-3\right)}^2=16.$

Câu 39: Đáp án A.

Lời giải

$\overrightarrow{\mathrm{AB}} = (-\mathrm{a}; \mathrm{b}; 0)$, $\overrightarrow{\mathrm{AC}} = (-\mathrm{a}; 0; \mathrm{c})$, $\overrightarrow{\mathrm{AD}}=\left(\mathrm{a}\sqrt{{\mathrm{b}}^2+{\mathrm{c}}^2}; \mathrm{b}\sqrt{{\mathrm{a}}^2+{\mathrm{c}}^2}; \mathrm{c}\sqrt{{\mathrm{a}}^2+{\mathrm{b}}^2}\right)$.

$\left[\overrightarrow{\mathrm{AB}},\overrightarrow{\mathrm{AC}}\right]=\left(\left|\begin{array}{cc}\mathrm{b}& 0\\ 0& \mathrm{c}\end{array}\right|;\left|\begin{array}{cc}0& -\mathrm{a}\\ \mathrm{c}& -\mathrm{a}\end{array}\right|;\left|\begin{array}{cc}-\mathrm{a}& \mathrm{b}\\ -\mathrm{a}& 0\end{array}\right|\right)=\left(\mathrm{bc};\mathrm{ac};\mathrm{ab}\right)$.

Vì diện tích tam giác ABC bằng $\frac{\sqrt{3}}{2}$ nên:

${\mathrm{S}}_{\mathrm{\Delta ABC}}=\frac{\sqrt{3}}{2}$$\iff \frac{1}{2}\left|\left[\overrightarrow{\mathrm{AB}},\overrightarrow{\mathrm{AC}}\right]\right|=\frac{\sqrt{3}}{2}$

$\iff \frac{1}{2}\sqrt{{\left(\mathrm{ab}\right)}^2+{\left(\mathrm{bc}\right)}^2+{\left(\mathrm{ac}\right)}^2}=\frac{\sqrt{3}}{2}$

$\iff {\left(\mathrm{ab}\right)}^2+{\left(\mathrm{bc}\right)}^2+{\left(\mathrm{ac}\right)}^2=3$.

Thể tích của tứ diện ABCD là:

$$\begin{gathered} {\mathrm{V}}_{\mathrm{ABCD}}=\frac{1}{6}\left|\left[\overrightarrow{\mathrm{AB}},\overrightarrow{\mathrm{AC}}\right].\overrightarrow{\mathrm{AD}}\right| \\ =\frac{1}{6}\left|\mathrm{abc}\sqrt{{\mathrm{b}}^2+{\mathrm{c}}^2}+\mathrm{abc}\sqrt{{\mathrm{a}}^2+{\mathrm{c}}^2}+\mathrm{abc}\sqrt{{\mathrm{a}}^2+{\mathrm{b}}^2}\right| \end{gathered}$$

$=\frac{1}{6}\left|\mathrm{bc}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{a}}^2{\mathrm{c}}^2}+\mathrm{ac}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{b}}^2{\mathrm{c}}^2}+\mathrm{ab}\sqrt{{\mathrm{a}}^2{\mathrm{c}}^2+{\mathrm{b}}^2{\mathrm{c}}^2}\right|$

Áp dụng bất đẳng thức Bunhiacopxki:

${(\mathrm{bc}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{a}}^2{\mathrm{c}}^2}+\mathrm{ac}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{b}}^2{\mathrm{c}}^2}+\mathrm{ab}\sqrt{{\mathrm{a}}^2{\mathrm{c}}^2+{\mathrm{b}}^2{\mathrm{c}}^2})}^2$

$\le \text{[}{\left(\mathrm{bc}\right)}^2+{\left(\mathrm{ac}\right)}^2+{\left(\mathrm{ab}\right)}^2\text{](}{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{a}}^2{\mathrm{c}}^2+{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{b}}^2{\mathrm{c}}^2+{\mathrm{a}}^2{\mathrm{c}}^2+{\mathrm{b}}^2{\mathrm{c}}^2)$

$$\begin{gathered} \iff {(\mathrm{bc}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{a}}^2{\mathrm{c}}^2}+\mathrm{ac}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{b}}^2{\mathrm{c}}^2}+\mathrm{ab}\sqrt{{\mathrm{a}}^2{\mathrm{c}}^2+{\mathrm{b}}^2{\mathrm{c}}^2})}^2 \\ \le 2{\text{[}{\left(\mathrm{bc}\right)}^2+{\left(\mathrm{ac}\right)}^2+{\left(\mathrm{ab}\right)}^2\text{]}}^2 \end{gathered}$$

$\iff {(\mathrm{bc}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{a}}^2{\mathrm{c}}^2}+\mathrm{ac}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{b}}^2{\mathrm{c}}^2}+\mathrm{ab}\sqrt{{\mathrm{a}}^2{\mathrm{c}}^2+{\mathrm{b}}^2{\mathrm{c}}^2})}^2\le 2{.3}^2$

$\iff {(\mathrm{bc}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{a}}^2{\mathrm{c}}^2}+\mathrm{ac}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{b}}^2{\mathrm{c}}^2}+\mathrm{ab}\sqrt{{\mathrm{a}}^2{\mathrm{c}}^2+{\mathrm{b}}^2{\mathrm{c}}^2})}^2\le 18$

$\iff \left|\mathrm{bc}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{a}}^2{\mathrm{c}}^2}+\mathrm{ac}\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2+{\mathrm{b}}^2{\mathrm{c}}^2}+\mathrm{ab}\sqrt{{\mathrm{a}}^2{\mathrm{c}}^2+{\mathrm{b}}^2{\mathrm{c}}^2}\right|\le 3\sqrt{2}$

${\mathrm{V}}_{\mathrm{A}.\mathrm{BCD}}\le \frac{3\sqrt{2}}{6}$ hay ${\mathrm{V}}_{\mathrm{A}.\mathrm{BCD}}\le \frac{\sqrt{2}}{2}$.

nên ${\mathrm{maxV}}_{\mathrm{A}.\mathrm{BCD}}=\frac{\sqrt{2}}{2}$. Dấu "=" xảy ra khi và chỉ khi a = b = c = 1.

Ta có:

$\overrightarrow{\mathrm{AC}}=\left(-1;0;1\right),\overrightarrow{\mathrm{AD}}=\left(\sqrt{2};\sqrt{2};\sqrt{2}\right)$.

Nên:

$$\begin{gathered} \left[\overrightarrow{\mathrm{AC}},\overrightarrow{\mathrm{AD}}\right]=\left(\left|\begin{array}{cc}0& 1\\ \sqrt{2}& \sqrt{2}\end{array}\right|;\left|\begin{array}{cc}1& -1\\ \sqrt{2}& \sqrt{2}\end{array}\right|;\left|\begin{array}{cc}-1& 0\\ \sqrt{2}& \sqrt{2}\end{array}\right|\right) \\ =\left(-\sqrt{2};2\sqrt{2};-\sqrt{2}\right) \end{gathered}$$.

Do đó:

${\mathrm{S}}_{\mathrm{\Delta ACD}}=\frac{1}{2}\left|\left[\overrightarrow{\mathrm{AC}},\overrightarrow{\mathrm{AD}}\right]\right|=\frac{1}{2}\sqrt{12}=\sqrt{3}$.

Vậy $\mathrm{d}(\mathrm{B},(\mathrm{ACD}\left)\right)=\frac{3{\mathrm{V}}_{\mathrm{A}.\mathrm{BCD}}}{{\mathrm{S}}_{\mathrm{\Delta ACD}}}=\frac{3.\frac{\sqrt{2}}{2}}{\sqrt{3}}=\frac{\sqrt{6}}{2}$.

Câu 40: Đáp án C.

Lời giải

Gọi $\mathrm{I}(\mathrm{m};\mathrm{n};\mathrm{p})$ là điểm thỏa mãn: $2\overrightarrow{\mathrm{IE}}-3\overrightarrow{\mathrm{IF}}=\overrightarrow{0}.$

Ta có:

$\overrightarrow{\mathrm{IE}}=(1-\mathrm{m};1-\mathrm{n};3-\mathrm{p});\overrightarrow{\mathrm{IF}}=(-\mathrm{m};1-\mathrm{n};-\mathrm{p}).$

$$\begin{gathered} 2\overrightarrow{\mathrm{IE}}-3\overrightarrow{\mathrm{IF}}=\overrightarrow{0}\iff \left\{\begin{array}{l}2(1-\mathrm{m})+3\mathrm{m}=0\\ 2(1-\mathrm{n})-3(1-\mathrm{n})=0\\ 2(3-\mathrm{p})+3\mathrm{p}=0\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{m}=-2\\ \mathrm{n}=1\\ \mathrm{p}=-6\end{array}\right.\Rightarrow \mathrm{I}(-2;1;-6). \end{gathered}$$

Ta có:

$$\begin{gathered} \left|2\overrightarrow{\mathrm{ME}}-3\overrightarrow{\mathrm{MF}}\right|=\left|2(\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{IE}})-3(\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{IF}})\right| \\ =\left|\overrightarrow{\mathrm{IM}}\right|=\mathrm{MI}. \end{gathered}$$

$\left|2\overrightarrow{\mathrm{ME}}-3\overrightarrow{\mathrm{MF}}\right|$ đạt giá trị nhỏ nhất, $\mathrm{M}\in \left(\mathrm{P}\right)$$\iff \mathrm{MI}$ nhỏ nhất, $\mathrm{M}\in \left(\mathrm{P}\right)$

$\iff \mathrm{M}$ là hình chiếu vuông góc của I trên ( P )

Khi đó :

$\overrightarrow{\mathrm{MI}}=\left(-2-\mathrm{a};1-\mathrm{b};-6-\mathrm{c}\right)$ cùng phương với vectơ pháp tuyến của ( P ) là $\overrightarrow{\mathrm{n}}=(1;1;1)$; $\mathrm{M}\in \left(\mathrm{P}\right)$

Tọa độ M là nghiệm của hệ:

$\left\{\begin{array}{l}\mathrm{a}-\mathrm{b}=-3\\ \mathrm{b}-\mathrm{c}=7\\ \mathrm{a}+\mathrm{b}+\mathrm{c}-1=0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{a}=\frac{2}{3}\\ \mathrm{b}=\frac{11}{3}\\ \mathrm{c}=\frac{-10}{3}\end{array}\right.\Rightarrow \mathrm{T}=3\text{a}+2\mathrm{b}+\mathrm{c}=6.$

Câu 41: Đáp án B.

Lời giải

Gọi M là trung điểm AB thì $\mathrm{M}\left(2;1;2\right)$,$\overrightarrow{\mathrm{AB}}=\left(2;-2;-6\right)$.

Mặt phẳng trung trực của đoạn AB đi qua M nhận $\overrightarrow{\mathrm{AB}}$ làm vectơ pháp tuyến, do đó nó có phương trình là:

$$\begin{gathered} 2\left(\mathrm{x}-2\right)-2\left(\mathrm{y}-1\right)-6\left(\mathrm{z}-2\right)=0 \\ \iff \mathrm{x}-\mathrm{y}-3\mathrm{z}+5=0. \end{gathered}$$

Câu 42: Đáp án D.

Lời giải

Gọi mặt phẳng cần tìm là mặt phẳng (Q).

Mặt phẳng (P) có một vectơ pháp tuyến là $\overrightarrow{\mathrm{n}}=\left(4;1;-1\right)$.

Vì (Q) // (P) nên $\overrightarrow{\mathrm{n}}=\left(4;1;-1\right)$ cũng là một vectơ pháp tuyến của mặt phẳng (Q).

Mặt phẳng (Q) đi qua điểm $\mathrm{A}\left(-1;2;4\right)$, có vectơ pháp tuyến $\overrightarrow{\mathrm{n}}=\left(4;1;-1\right)$ nên nó có phương trình là:

$4\left(\mathrm{x}+1\right)+1.\left(\mathrm{y}-2\right)-1.\left(\mathrm{z}-4\right)=0$

$\iff$$4\mathrm{x}+\mathrm{y}-\mathrm{z}+6=0$

Câu 43: Đáp án C.

Lời giải

Ta có:  ${\overrightarrow{\mathrm{n}}}_{\left(\mathrm{Q}\right)}=\left(1;-3;1\right)$ là một vectơ pháp tuyến của (Q).

            ${\overrightarrow{\mathrm{n}}}_{\left(\mathrm{R}\right)}=\left(2;-1;3\right)$ là một vectơ pháp tuyến của (R).

Vì $\left(\mathrm{P}\right)\perp \left(\mathrm{Q}\right)$ nên ${\overrightarrow{\mathrm{n}}}_{\left(\mathrm{P}\right)}\perp {\overrightarrow{\mathrm{n}}}_{\left(\mathrm{Q}\right)}$,

     $\left(\mathrm{P}\right)\perp \left(\mathrm{R}\right)$ nên ${\overrightarrow{\mathrm{n}}}_{\left(\mathrm{P}\right)}\perp {\overrightarrow{\mathrm{n}}}_{\left(\mathrm{R}\right)}$.

$\Rightarrow$${\overrightarrow{\mathrm{n}}}_{\left(\mathrm{P}\right)}=\left[{\overrightarrow{\mathrm{n}}}_{\left(\mathrm{Q}\right)},{\overrightarrow{\mathrm{n}}}_{\left(\mathrm{R}\right)}\right]=\left(-8;-1;5\right)$ một vectơ pháp tuyến của (P).

(P) đi qua điểm $\mathrm{M}\left(-4;1;2\right)$ có vectơ pháp tuyến là ${\overrightarrow{\mathrm{n}}}_{\left(\mathrm{P}\right)}=\left(-8;-1;5\right)$ nên nó có phương trình là:

 $-8\left(\mathrm{x}+4\right)-\left(\mathrm{y}-1\right)+5\left(\mathrm{z}-2\right)=0$

$\iff$$-8\mathrm{x}-\mathrm{y}+5\mathrm{z}-41=0$

$\iff$$8\mathrm{x}+\mathrm{y}-5\mathrm{z}+41=0$

Câu 44: Đáp án A.

Lời giải

(S) có tâm $\mathrm{I}\left(-1;2;1\right)$, bán kính R = 3.

Dễ thấy $\mathrm{A}\in \left(\mathrm{S}\right)$.

Vì (P) tiếp xúc với (S) tại A nên  $\overrightarrow{\mathrm{IA}}=\left(2;1;-2\right)$ là một vectơ pháp tuyến của (P).

Ta có (P) đi qua $\mathrm{A}\left(1;3;-1\right)$ nhận $\overrightarrow{\mathrm{IA}}=\left(2;1;-2\right)$ làm vectơ pháp tuyến nên (P) có phương trình là:

$2\left(\mathrm{x}-1\right)+1.\left(\mathrm{y}-3\right)-2\left(\mathrm{z}+1\right)=0$

$\iff$$2\mathrm{x}+\mathrm{y}-2\mathrm{z}-7=0$

Câu 45: Đáp án D.

Lời giải

Ta có  $\overrightarrow{\mathrm{AB}}\left(-2;-1;5\right)$, (P) nhận $\overrightarrow{{\mathrm{n}}_{\left(\mathrm{P}\right)}}\mathrm{\hspace{0.17em}}=\mathrm{\hspace{0.17em}}\left(2\mathrm{\hspace{0.17em}};\mathrm{\hspace{0.17em}}-\mathrm{\hspace{0.17em}}1\mathrm{\hspace{0.17em}};\mathrm{\hspace{0.17em}}2\right)$ làm vectơ pháp tuyến.

Do (Q) qua A, B và vuông góc với (P) nên (Q) nhận $\left[\overrightarrow{\mathrm{AB}}\mathrm{\hspace{0.17em}},\mathrm{\hspace{0.17em}}\overrightarrow{{\mathrm{n}}_{\left(\mathrm{P}\right)}}\right]\mathrm{\hspace{0.17em}}=\mathrm{\hspace{0.17em}}\left(3\mathrm{\hspace{0.17em}};\mathrm{\hspace{0.17em}}14\mathrm{\hspace{0.17em}};\mathrm{\hspace{0.17em}}4\right)$ làm vectơ pháp tuyến, tức (Q) có phương trình là:

$$\begin{gathered} 3\left(\mathrm{x}-1\right)+14\mathrm{y}+4\left(\mathrm{z}+2\right)=0 \\ \iff 3\mathrm{x}+14\mathrm{y}+4\mathrm{z}+5=0 \end{gathered}$$

$\Rightarrow \mathrm{a}=3,\mathrm{b}=-14,\mathrm{c}=4$.

Vậy a + b + c = -7.

Câu 46: Đáp án A.

Lời giải

Ta có: $\overrightarrow{\mathrm{AB}}=\left(2;-3;-1\right), \overrightarrow{\mathrm{AC}}=\left(-2;0;-2\right)$

Vì $\left[\overrightarrow{\mathrm{AB}}\mathrm{\hspace{0.17em}},\mathrm{\hspace{0.17em}}\overrightarrow{\mathrm{AC}}\right]\mathrm{\hspace{0.17em}}=\mathrm{\hspace{0.17em}}\left(6\mathrm{\hspace{0.17em}};\mathrm{\hspace{0.17em}}6\mathrm{\hspace{0.17em}};\mathrm{\hspace{0.17em}}-\mathrm{\hspace{0.17em}}6\right)\mathrm{\hspace{0.17em}}$nên một vectơ pháp tuyến của (ABC) là:

$\overrightarrow{\mathrm{n}}=\left(1;1;-1\right)$.

Ta có (ABC) qua A(0; 1; 2) và nhận $\overrightarrow{\mathrm{n}}=\left(1;1;-1\right)$ làm vectơ pháp tuyến nên (ABC) có phương trình là:

$$\begin{gathered} 1\left(\mathrm{x}-0\right)+1\left(\mathrm{y}-1\right)-1\left(\mathrm{z}-2\right)=0 \\ \iff \mathrm{x}+\mathrm{y}-\mathrm{z}+1=0 \end{gathered}$$

Câu 47: Đáp án A.

Lời giải

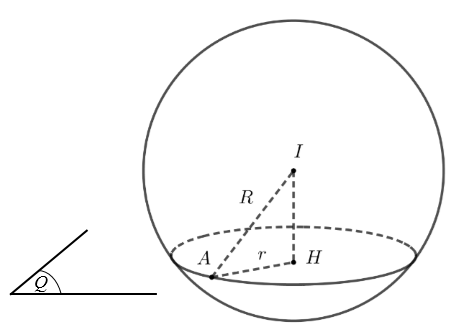
Vì (Q) // (P) nên phương trình mặt phẳng (Q) có dạng:

$2\mathrm{x}-2\mathrm{y}+\mathrm{z}+\mathrm{D}=0$ $\left(\mathrm{D}\ne 17\right)$.

Mặt cầu (S) có tâm $\mathrm{I}\left(0;2;-1\right)$, bán kính R = 5.

Trên hình vẽ, ta có tam giác $\mathrm{\Delta IHA}$ vuông tại H 

$\Rightarrow {\mathrm{IH}}^2+{\mathrm{r}}^2={\mathrm{R}}^2$

$\iff {\left[\mathrm{d}\left(\mathrm{I},\left(\mathrm{Q}\right)\right)\right]}^2+{\mathrm{r}}^2={\mathrm{R}}^2$

$\iff \mathrm{d}\left(\mathrm{I},\left(\mathrm{Q}\right)\right)=\sqrt{{\mathrm{R}}^2-{\mathrm{r}}^2}\Rightarrow \mathrm{d}\left(\mathrm{I},\left(\mathrm{Q}\right)\right)=\sqrt{5^2-3^2}=4$

$\Rightarrow \frac{\left|2.0-2.2-1+\mathrm{D}\right|}{\sqrt{2^2+{\left(-2\right)}^2+1^2}}=4$$\iff \left|\mathrm{D}-5\right|=12$

$\iff \left[\begin{array}{l}\mathrm{D}-5=12\\ \mathrm{D}-5=-12\end{array}\right.$$\iff \left[\begin{array}{l}\mathrm{D}=17\\ \mathrm{D}=-7\end{array}\right.$(loại D = 17).

Vậy phương trình mặt phẳng (Q) là: 2x – 2y + z – 7 = 0.

Câu 48: Đáp án C.

Lời giải

Mặt phẳng $\left(\mathrm{\alpha }\right):\mathrm{y}=0$ có vectơ pháp tuyến $\overrightarrow{\mathrm{n}}=\left(0;1;0\right)$và đi qua gốc tọa độ nên nó trùng với mặt phẳng (Oxz).

Câu 49: Đáp án C.

Lời giải

Phương trình mặt phẳng (ABC):

 $\frac{\mathrm{x}}{1}+\frac{\mathrm{y}}{2}+\frac{\mathrm{z}}{4}=1\iff 4\mathrm{x}+2\mathrm{y}+\mathrm{z}-4=0$

Khi đó:

$\mathrm{d}\left(\mathrm{M},\left(\mathrm{ABC}\right)\right)=\frac{\left|0+0+3-4\right|}{\sqrt{4^2+2^2+1^2}}=\frac{1}{\sqrt{21}}$.

Câu 50: Đáp án D.

Lời giải

Vì MA = MB nên M thuộc mặt phẳng trung trực (Q) của đoạn thẳng AB.

Ta có (Q) đi qua trung điểm $\mathrm{I}(3;1;-1)$ của AB và có véctơ pháp tuyến là $\overrightarrow{\mathrm{AB}}=(2;4;-2)$ nên (Q) có phương trình là:

$2(\mathrm{x}-3)+4(\mathrm{y}-1)-2(\mathrm{z}+1)=0\iff \mathrm{x}+2\mathrm{y}-\mathrm{z}-6=0.$

Vì $\mathrm{M}\in \left(\mathrm{P}\right)$ và $\mathrm{M}\in \left(\mathrm{Q}\right)$ nên M thuộc giao tuyến ∆ của (P) và (Q).

(P) có véctơ pháp tuyến ${\overrightarrow{\mathrm{n}}}_{\left(\mathrm{P}\right)}=(0;0;1)$, (Q) có véctơ pháp tuyến:

${\overrightarrow{\mathrm{n}}}_{\left(\mathrm{Q}\right)}=(1;2;-1)$.

Khi đó ∆ có véctơ chỉ phương $\overrightarrow{\mathrm{u}}=[{\overrightarrow{\mathrm{n}}}_{\left(\mathrm{P}\right)},{\overrightarrow{\mathrm{n}}}_{\left(\mathrm{Q}\right)}]=(-2;1;0)$.

Chọn N(2; 2; 0) là một điểm chung của (P) và (Q).

∆ đi qua N nên có phương trình $\left\{\begin{array}{l}\mathrm{x}=2-2\mathrm{t}\\ \mathrm{y}=2+\mathrm{t}\\ \mathrm{z}=0\end{array}\right.(\mathrm{t}\in \mathrm{ℝ})$.

Vì $\mathrm{M}\in \mathrm{\Delta }$ nên $\mathrm{M}=(2-2\mathrm{t};2+\mathrm{t};0)$. Theo định lý cosin trong tam giác MAB, ta có:

$$\begin{gathered} \cos \widehat{\mathrm{AMB}}=\frac{{\mathrm{MA}}^2+{\mathrm{MB}}^2-{\mathrm{AB}}^2}{2\mathrm{MA}\cdot \mathrm{MB}} \\ =\frac{2{\mathrm{MA}}^2-{\mathrm{AB}}^2}{2{\mathrm{MA}}^2}=1-\frac{{\mathrm{AB}}^2}{2{\mathrm{MA}}^2}. \end{gathered}$$

Vì AB không đổi nên từ biểu thức trên ta có $\widehat{\mathrm{AMB}}$ lớn nhất

$\iff \cos \widehat{\mathrm{AMB}}$ nhỏ nhất $\iff {\mathrm{MA}}^2$  nhỏ nhất.

Ta có:

$$\begin{gathered} {\mathrm{MA}}^2={\left(2\mathrm{t}\right)}^2+{\left(\mathrm{t}+3\right)}^2=5{\mathrm{t}}^2+6\mathrm{t}+9 \\ =5{\left(\mathrm{t}+\frac{3}{5}\right)}^2+\frac{36}{5}\ge \frac{36}{5} \end{gathered}$$

Đẳng thức xảy ra $\iff \mathrm{t}=-\frac{3}{5}$, khi đó $\mathrm{M}\left(\frac{16}{5};\frac{7}{5};0\right)$.

Vậy $\mathrm{a}+\mathrm{b}=\frac{23}{5}$.

Đề thi Giữa học kì 2 Toán lớp 12 có đáp án - đề số 2

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa học kì 2

Năm học ...

Môn: Toán 12

Thời gian làm bài: 90 phút

Câu 1: Cho hàm số y = f(x) liên tục trên $\mathrm{ℝ}$ và có bảng xét dấu của đạo hàm như hình vẽ:

         

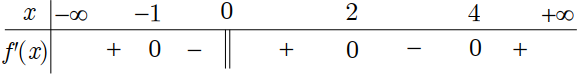
Hàm số đã cho đồng biến trong khoảng nào dưới đây?

A. $\left(2;4\right)$

B. $\left(-\infty ;0\right)$

C. (0; 2)

D. (-1; 2)

Câu 2: Phương trình đường tiệm cận ngang của đồ thị hàm số $\mathrm{y}=\frac{4-3\mathrm{x}}{\mathrm{x}+1}$ là:

A. x = -3

B.  x = -1

C.  y = -3

D.  y = 4

Câu 3: Cho hàm số y = f(x) có bảng biến thiên như sau:

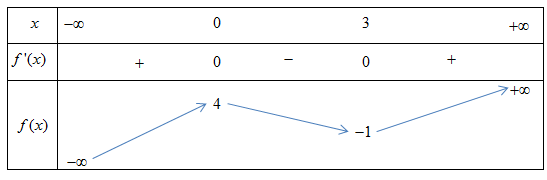
Mệnh đề nào sau đây đúng ?

A. Đồ thị hàm số có 2 đường tiệm cận ngang.

B. Đồ thị hàm số có đường tiệm cận ngang y = 4.

C. Đồ thị hàm số không có tiệm cận.

D. Đồ thị hàm số  có đường tiệm cận đứng x = 0.

Câu 4: Cho hàm số y = e^x. Mệnh đề nào sau đây sai ?

A. Đồ thị hàm số đi qua điểm A(1; 0).

B. Tập xác định của hàm số là$\mathrm{D}=\mathrm{ℝ}$.

C. Hàm số có đạo hàm$\mathrm{y}\text{'}={\mathrm{e}}^{\mathrm{x}},\forall \mathrm{x}\in \mathrm{ℝ}$.

D. Đồ thị hàm số nhận trục hoành là tiệm cận ngang.

Câu 5: Cho hình lập phương $\mathrm{ABCD}.\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}\mathrm{D}\text{'}$ có cạnh bằng 2a. Khoảng cách giữa hai đường thẳng AB'và CD' bằng

A. 2a

B. a

C. $2\sqrt{2}\mathrm{a}$

D. $\sqrt{2}\mathrm{a}$

Câu 6: Cho hình hộp chữ nhật $\mathrm{ABCD}.\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}\mathrm{D}\text{'}$ có $\mathrm{BA}=\mathrm{a};\mathrm{BC}=2\mathrm{a};\mathrm{BB}\text{'}=3\mathrm{a}$. Thể tích V của khối hộp chữ nhật $\mathrm{ABCD}.\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}\mathrm{D}\text{'}$ bằng

A. $\mathrm{V}=2{\mathrm{a}}^3$

B. $\mathrm{V}=3{\mathrm{a}}^3$

C. $\mathrm{V}=6{\mathrm{a}}^3$

D. $\mathrm{V}={\mathrm{a}}^3$

Câu 7: Cho khối lăng trụ $\mathrm{ABC}.{\mathrm{A}}^{\text{'}}{\mathrm{B}}^{\text{'}}{\mathrm{C}}^{\text{'}}$ có diện tích đáy bằng 2a², đường cao bằng 3a. Thể tích khối lăng trụ $\mathrm{ABC}.{\mathrm{A}}^{\text{'}}{\mathrm{B}}^{\text{'}}{\mathrm{C}}^{\text{'}}$ là.

A. ${\mathrm{a}}^3$

B. $6{\mathrm{a}}^3$

C. $12{\mathrm{a}}^3$

D. $2{\mathrm{a}}^3$

Câu 8: Cho hàm số f(x) xác định trên $\mathrm{ℝ}\backslash \left\{0\right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau

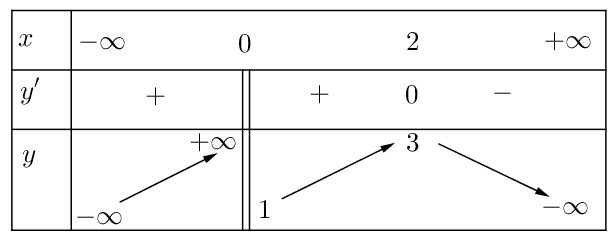
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m – 1 có ba nghiệm thực phân biệt.

A. $\mathrm{m}\in \left(2;4\right)$

B. $\mathrm{m}\in \left[2;4\right)$

C. $\mathrm{m}\in \left(1;3\right)$

D. $\mathrm{m}\in \left[1;3\right)$

Câu 9: Thể tích của khối cầu có bán kính R là

A. $\frac{4}{3}{\mathrm{\pi R}}^3$

B. $\frac{4}{3}{\mathrm{R}}^3$

C. $4{\mathrm{\pi R}}^3$

D. $\frac{3}{4}{\mathrm{\pi R}}^3$

Câu 10: Tìm $\int \frac{1}{\mathrm{x}}\text{d}\mathrm{x}$?

A. $\int \frac{1}{\mathrm{x}}\text{d}\mathrm{x}=\ln \left|\mathrm{x}\right|+\mathrm{C}$

B. $\int \frac{1}{\mathrm{x}}\text{d}\mathrm{x}=-\ln \left|\mathrm{x}\right|+\mathrm{C}$

C. $\int \frac{1}{\mathrm{x}}\text{d}\mathrm{x}=\frac{1}{{\mathrm{x}}^2}+\mathrm{C}$

D. $\int \frac{1}{\mathrm{x}}\text{d}\mathrm{x}=-\frac{1}{{\mathrm{x}}^2}+\mathrm{C}$

Câu 11: Khối bát diện đều là khối đa diện đều loại

A. {4; 3}

B. {3; 4}

C. {3; 3}

D. {3; 5}

Câu 12: Trong không gian Oxyz, Cho $\overrightarrow{\mathrm{u}}=2\overrightarrow{\mathrm{i}}-3\overrightarrow{\mathrm{j}}-2\overrightarrow{\mathrm{k}}$. Tọa độ vectơ $\overrightarrow{\mathrm{u}}$ là

A. $\left(2;-3;2\right)$

B. $\left(2;-3;-2\right)$

C. $\left(2;3;2\right)$

D. $\left(-2;-3;2\right)$

Câu 13: Cho hàm số y = f(x) liên tục trên $\mathrm{ℝ}$ và có bảng biến thiên như sau

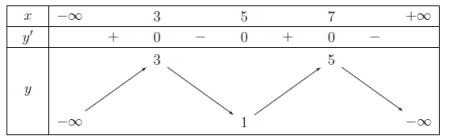
Mệnh đề nào sau đây sai?

A. Đồ thị hàm số không có tiệm cận.

B. Gía trị cực tiểu của hàm số bằng 1.

C. x = 5 là điểm cực đại của hàm số.

D. Hàm số có ba điểm cực trị.

Câu 14: Biểu thức ${\mathrm{a}}^{\frac{8}{3}}:\sqrt[3]{{\mathrm{a}}^4}$ viết dưới dạng luỹ thừa với số mũ hữu tỷ là

A. ${\mathrm{a}}^{\frac{9}{8}}$

B. ${\mathrm{a}}^{\frac{3}{4}}$

C. ${\mathrm{a}}^4$

D. ${\mathrm{a}}^{\frac{4}{3}}$

Câu 15: Tập xác định của hàm số $\mathrm{y}={\log }_{2021}\mathrm{x}$ là

A. $\mathrm{D}=\left(2021;+\infty \right)$

B. $\mathrm{D}=\left(0;+\infty \right)$

C. $\mathrm{D}=\left[0;+\infty \right)$

D. $\left(0;+\infty \right)\backslash \left\{1\right\}$

Câu 16: Hàm số nào sau đây đồng biến trên R?

A. $\mathrm{y}={\mathrm{x}}^4+2{\mathrm{x}}^2$

B. $\mathrm{y}=\frac{\mathrm{x}-1}{\mathrm{x}+1}$

C. $\mathrm{y}=-{\mathrm{x}}^3-3\mathrm{x}+1$

D. $\mathrm{y}=2{\mathrm{x}}^3+3\mathrm{x}+1$

Câu 17: Hàm số nào sau đây là một nguyên hàm của hàm số $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{x}}^2$?

A. $\mathrm{F}\left(\mathrm{x}\right)=3{\mathrm{x}}^3$

B. $\mathrm{F}\left(\mathrm{x}\right)=\frac{{\mathrm{x}}^3}{3}$

C. $\mathrm{F}\left(\mathrm{x}\right)=\frac{{\mathrm{x}}^3}{2}$

D. $\mathrm{F}\left(\mathrm{x}\right)=2\mathrm{x}$

Câu 18: Tập nghiệm S của bất phương trình $9^{\mathrm{x}+\frac{1}{2}}-10{.3}^{\mathrm{x}}+3\le 0$.

A. $\mathrm{S}=\left\{-1;1\right\}$

B. $\mathrm{S}=\left(-1;1\right)$

C. $\mathrm{S}=\left[-1;1\right]$

D. $\mathrm{S}=(-\infty ;-1]\cup \text{[}1;+\infty )$

Câu 19: Trong không gian Oxyz, cho các điểm $\mathrm{A}\left(2;0;0\right),\mathrm{B}\left(0;4;0\right),\mathrm{C}\left(0;0;6\right)$. Tính thể tích V của tứ diện OABC?

A. V = 48 (đvtt)

B. V = 24 (đvtt)

C. V = 8 (đvtt)

D. V = 16 (đvtt)

Câu 20: Cho cấp số cộng $\left({\mathrm{u}}_{\mathrm{n}}\right)$ có ${\mathrm{u}}_3=-7$ và ${\mathrm{u}}_4=-4$. Tìm công sai d của cấp số cộng đã cho.

A. d = 3

B. $\mathrm{d}=\frac{4}{7}$

C. $\mathrm{d}=-11$

D. $\mathrm{d}=-3$

Câu 21: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $\mathrm{y}=\frac{\mathrm{x}+1}{{\mathrm{x}}^2-3\mathrm{x}-4}$.

A. 3

B. 1

C. 2

D. 0

Câu 22: Số cách chọn đồng thời 4 người từ một nhóm có 11 người là

A. 44

B. ${\mathrm{A}}_{11}^4$

C. 15

D. ${\mathrm{C}}_{11}^4$

Câu 23: Cho hàm số f(x) liên tục trên R và có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số đã cho trên [-2; 0] là:

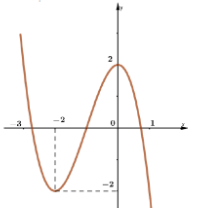
A. -1

B. 0

C. 2

D. -2.

Câu 24: Cho hàm số f(x) liên tục trên R và có đồ thị như hình vẽ. Điểm cực đại của hàm số là:

A. x = 3

B. x = 1

C. x = 0

D. x = -1

Câu 25: Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất trên đoạn [0; 1] của hàm số $\mathrm{y}=2{\mathrm{x}}^3-3{\mathrm{x}}^2+{2020}^{2021}$. Giá trị của biểu thức P = M – m bằng

A. -1

B. 1

C. ${2020}^{2021}+1$

D. ${2020}^{2021}-1$

Câu 26: Cho b là số thực dương tùy ý. Mệnh đề nào sau đây sai?

A. ${\log }_5\left(5\mathrm{b}\right)=1+{\log }_5\mathrm{b}$

B. ${\log }_5\left(\frac{5}{\mathrm{b}}\right)=1-{\log }_5\mathrm{b}$

C. ${\log }_5\left({\mathrm{b}}^5\right)=5{\log }_5\mathrm{b}$

D. ${\log }_5\sqrt[5]{\mathrm{b}}=5{\log }_5\mathrm{b}$

Câu 27: Cho hình nón có bán kính đáy bằng r, đường sinh bằng l và chiều cao bằng h. Diện tích xung quanh của hình nón đó bằng

A. $2\mathrm{\pi rh}$

B. $\mathrm{\pi rh}$

C. $2\mathrm{\pi rl}$

D. $\mathrm{\pi rl}$

Câu 28: Tập xác định của hàm số $\mathrm{f}\left(\mathrm{x}\right)={\left({\mathrm{x}}^2-4\right)}^{-2}+{\log }_{\sqrt{3}}\left(2\mathrm{x}+1\right)$ là:

A. $\mathrm{ℝ}\backslash \left\{\pm \sqrt{2}\right\}$

B. $\left(-\frac{1}{2};+\infty \right)$

C. $\left(2;+\infty \right)$

D. $\left(-\frac{1}{2};+\infty \right)\backslash \left\{2\right\}$

Câu 29: Phương trình $4^{\mathrm{x}-1}=16$ có nghiệm là:

A. x = 4

B. x = 2

C. x = 5

D. x = 3

Câu 30: Đồ thị hàm số nào dưới đây là đường cong trong hình bên?

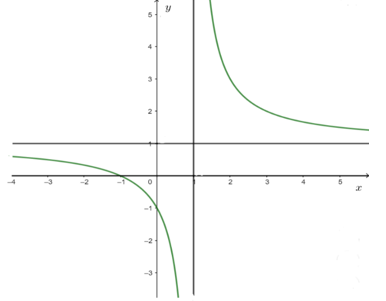
A. $\mathrm{y}=\frac{\mathrm{x}-1}{\mathrm{x}+1}$

B. $\mathrm{y}=\frac{\mathrm{x}+1}{\mathrm{x}-1}$

C. $\mathrm{y}=\frac{\mathrm{x}}{\mathrm{x}-1}$

D. $\mathrm{y}=\frac{\mathrm{x}}{\mathrm{x}+1}$

Câu 31: Trong không gian Oxyz, cho $\mathrm{A}\left(1;0;-2\right),\mathrm{B}\left(2;-3;1\right)$. Tọa độ vectơ $\overrightarrow{\mathrm{BA}}$ là

A. $\left(3;-3;-1\right)$

B. $\left(-1;3;-3\right)$

C. $\left(1;-3;-3\right)$

D. $\left(1;-3;3\right)$

Câu 32: Cắt một hình trụ bằng một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông cạnh 3a. Diện tích xung quanh của hình trụ đó là:

A. $18{\mathrm{\pi a}}^2$

B. $\frac{9{\mathrm{\pi a}}^2}{2}$

C. $36{\mathrm{\pi a}}^2$

D. $9{\mathrm{\pi a}}^2$

Câu 33: Trong không gian Oxyz, cho hai điểm $\mathrm{A}\left(1;2;0\right),\mathrm{B}\left(-1;3;5\right)$ . Gọi I(a; b; c) là điểm thỏa mãn $\overrightarrow{\mathrm{IA}}+3\overrightarrow{\mathrm{IB}}=\overrightarrow{0}$. Khi đó, giá trị của biểu thức a + 2b + 2c bằng:

A. $\frac{25}{2}$

B. $-\frac{25}{2}$

C. 50

D. $\frac{27}{2}$

Câu 34: Cho a, b là số thực dương và a > 1, a ≠ b thỏa mãn ${\log }_{\mathrm{a}}\mathrm{b}=3$. Giá trị của biểu thức $\mathrm{T}=\frac{{\mathrm{b}}^3}{{\mathrm{a}}^9}+{\log }_{\frac{\mathrm{a}}{\mathrm{b}}}\sqrt{\mathrm{ab}}$ bằng:

A. -3

B. 0

C. 5

D. 2

Câu 35: Biết $\int \mathrm{f}\left(\mathrm{u}\right)\mathrm{du}=\mathrm{F}\left(\mathrm{u}\right)+\mathrm{C}$. Với mọi số thực a ≠ 0, mệnh đề nào sau đây đúng?

A. $\int \mathrm{f}\left(\mathrm{ax}+\mathrm{b}\right)\mathrm{dx}=\frac{1}{\mathrm{a}}\mathrm{F}\left(\mathrm{ax}+\mathrm{b}\right)+\mathrm{C}$

B. $\int \mathrm{f}\left(\mathrm{ax}+\mathrm{b}\right)\mathrm{dx}=\mathrm{F}\left(\mathrm{ax}+\mathrm{b}\right)+\mathrm{C}$

C. $\int \mathrm{f}\left(\mathrm{ax}+\mathrm{b}\right)\mathrm{dx}=\mathrm{aF}\left(\mathrm{ax}+\mathrm{b}\right)+\mathrm{C}$

D. $\int \mathrm{f}\left(\mathrm{ax}+\mathrm{b}\right)\mathrm{dx}=\mathrm{aF}\left(\mathrm{x}+\mathrm{b}\right)+\mathrm{C}$

Câu 36: Cho hàm số  $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{ax}}^3+{\mathrm{bx}}^2+\mathrm{cx}+\mathrm{d}$,  (a, b, c, d là các số thực a ≠ 0) có đồ thị $\mathrm{f}\text{'}\left(\mathrm{x}\right)$ như hình bên. Có bao nhiêu giá trị thực của tham số m để hàm số $\mathrm{y}=\mathrm{f}\left({\mathrm{x}}^2+2\mathrm{x}\right)+{2021}^{\mathrm{m}}\left(\mathrm{lnx}-\frac{1}{\mathrm{x}}\right)$ nghịch biến trên nửa khoảng $\left[1;+\infty \right)$?

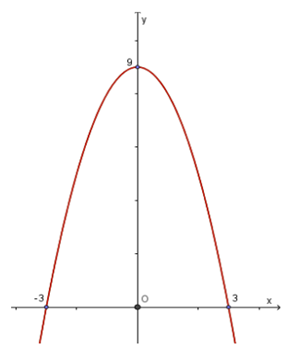
A. 0

B. 1

C. 2020

D. 2021

Câu 37: Cho hình lăng trụ $\mathrm{ABC}.{\mathrm{A}}^{\text{'}}{\mathrm{B}}^{\text{'}}{\mathrm{C}}^{\text{'}}$ có đáy là tam giác vuông cân tại B với AB = a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) là điểm H trên cạnh AB sao cho HA = 2HB. Biết ${\mathrm{A}}^{\text{'}}\mathrm{H}=\frac{\mathrm{a}\sqrt{2}}{3}$. Tính khoảng cách giữa đường thẳng AA' và BC theo a.

A. $\frac{\mathrm{a}\sqrt{3}}{6}$

B. $\frac{\mathrm{a}\sqrt{3}}{3}$

C. $\frac{\mathrm{a}\sqrt{3}}{2}$

D. $\frac{2\mathrm{a}\sqrt{3}}{3}$

Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a. Biết $\mathrm{SA}\perp \left(\mathrm{ABCD}\right), \mathrm{SA}=\mathrm{a}$. Gọi E là điểm thỏa mãn $\overrightarrow{\mathrm{SE}}=\overrightarrow{\mathrm{BC}}$. Góc giữa (BED) và (SBC) bằng 60°. Bán kính mặt cầu ngoại tiếp tứ diện SCDE bằng

A. $\frac{\mathrm{a}\sqrt{3}}{2}$

B. $\frac{\mathrm{a}\sqrt{2}}{2}$

C. $\mathrm{a}\sqrt{3}$

D. $\mathrm{a}\sqrt{2}$

Câu 39: Trong không gian Oxyz, cho hình chóp S.ABC có $\mathrm{S}\left(2;3;1\right)$ và $\mathrm{G}\left(-1;2;0\right)$ là trọng tâm tam giác ABC. Gọi $\mathrm{A}\text{'}, \mathrm{B}\text{'}, \mathrm{C}\text{'}$ lần lượt là các điểm thuộc các cạnh SA, SB, SC sao cho $\frac{\mathrm{SA}\text{'}}{\mathrm{SA}}=\frac{1}{3};\frac{\mathrm{SB}\text{'}}{\mathrm{SB}}=\frac{1}{4};\frac{\mathrm{SC}\text{'}}{\mathrm{SC}}=\frac{1}{5}$. Mặt phẳng $\left(\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}\right)$ cắt SG tại G'. Giả sử $\mathrm{G}\text{'}\left(\mathrm{a};\mathrm{b};\mathrm{c}\right)$. Giá trị của biểu thức a + b + c bằng

A. $\frac{19}{4}$

B. $\frac{29}{4}$

C. 1

D. -14

Câu 40: Gọi S là tập hợp tất cả các số tự nhiên gồm 8 chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn có chữ số hàng đơn vị chia hết cho 3 và tổng các chữ số của số đó chia hết cho 13?

A. $\frac{1}{18}$

B. $\frac{1}{36}$

C. $\frac{1}{9}$

D. $\frac{1}{72}$

Câu 41: Cho hàm số y = f(x) có đạo hàm liên tục trên R và bảng biến thiên của hàm số $\mathrm{f}\text{'}\left(\mathrm{x}\right)$ như sau:

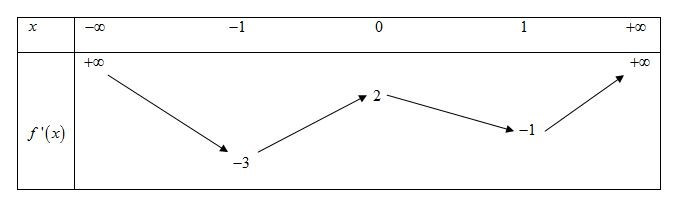
Hỏi hàm số $\mathrm{g}\left(\mathrm{x}\right)=\mathrm{f}\left(\left|\frac{\ln ({\mathrm{x}}^2+1)-2}{2}\right|\right)$ có bao nhiêu điểm cực tiểu ?

A. 9

B. 4

C. 7

D. 5

Câu 42: Cho hàm số $\mathrm{y}=\frac{2\mathrm{x}+\mathrm{m}}{\mathrm{x}-4}$ (m là tham số thực ) Thỏa mãn $\underset{\left[0;2\right]}{\max }\mathrm{y}=3$. Mệnh đề nào dưới đây là đúng ?

A. $\mathrm{m}<-11$

B. $\mathrm{m} = -12$

C. $\mathrm{m}> -8$

D. $\mathrm{m}<-8$

Câu 43: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Gọi M, K lần lượt là trọng tâm tam giác SAB, SCD; N là trung điểm của BC. Thể tích khối tứ diện S.MNK bằng

A. $\frac{2{\mathrm{a}}^3}{27}$

B. $\frac{{\mathrm{a}}^3}{27}$

C. $\frac{4{\mathrm{a}}^3}{27}$

D. $\frac{8{\mathrm{a}}^3}{27}$

Câu 44: Có bao nhiêu giá trị nguyên âm của tham số m để hàm số $\mathrm{y}=\mathrm{x}+3-\frac{\mathrm{m}}{\mathrm{x}-2}$ đồng biến trên $\left[5;+\infty \right)$?
A. 3

B. 2

C. 8

D. 9

Câu 45: Cho hình nón có chiều cao bằng 3a, biết rằng khi cắt hình nón đã cho bởi một mặt phẳng đi qua đỉnh hình nón và cách tâm của đáy hình nón một khoảng bằng a, thiết diện thu được là một tam giác vuông. Tính thể tích của khối nón được giởi hạn bởi hình nón đã cho bằng:

A. $15{\mathrm{\pi a}}^3$

B. $9{\mathrm{\pi a}}^3$

C. $\frac{45{\mathrm{\pi a}}^3}{4}$

D. $12{\mathrm{\pi a}}^3$

Câu 46. Cho phương trình ${\left({\log }_3\left(\frac{\mathrm{x}}{3}\right)\right)}^2+3{\mathrm{mlog}}_3\mathrm{x}+2{\mathrm{m}}^2-2\mathrm{m}-1=0$ (m là tham số). Có bao nhiêu giá trị nguyên của tham số m lớn hơn -2021 sao cho phương trình đã cho có hai nghiệm phân biệt x1, x2 thỏa mãn ${\mathrm{x}}_1+{\mathrm{x}}_2>10$?

A. 2022

B. 2019

C. 2020

D. 2021

Câu 47: Cho hàm số $\mathrm{f}\left(\mathrm{x}\right)=\frac{2}{\mathrm{sinx}}.$ Biết F(x) là một nguyên hàm của hàm số f(x) thỏa mãn $\mathrm{F}\left(\frac{\mathrm{\pi }}{2}\right)=0.$ Giá trị lớn nhất của hàm số $\mathrm{g}\left(\mathrm{x}\right)={\mathrm{e}}^{\mathrm{F}\left(\mathrm{x}\right)}$ trên đoạn $\left[\frac{\mathrm{\pi }}{6};\frac{2\mathrm{\pi }}{3}\right]$ bằng

A. 3

B. $\frac{1}{3}$

C. $7-4\sqrt{3}$

D. $7+4\sqrt{3}$

Câu 48: Biết rằng F(x) là một nguyên hàm trên R của hàm số $\mathrm{f}\left(\mathrm{x}\right)=\frac{2021\mathrm{x}}{{\left({\mathrm{x}}^2+1\right)}^{2022}}$ thỏa mãn $\mathrm{F}\left(0\right)=-\frac{1}{2}$. Giá trị nhỏ nhất của hàm số F(x)  bằng

A. $\frac{1}{2}$

B. $-\frac{1}{2}$

C. $\frac{2021}{2}$

D. $-\frac{2021}{2}$

Câu 49: Trong không gian Oxyz, cho các điểm $\mathrm{A}\left(-3;0;0\right)$, $\mathrm{B}\left(0;-4;0\right)$. Gọi I, J lần lượt là tâm đường tròn nội tiếp và ngoại tiếp của tam giác OAB. Tính độ dài đoạn thẳng IJ

A. $\frac{\sqrt{5}}{2}$

B. $\frac{5}{4}$

C. $\frac{\sqrt{61}}{6}$

D. $\frac{\sqrt{61}}{2}$

Câu 50: Cho hàm số f(x) liên tục trên R và có đồ thị như hình dưới đây:

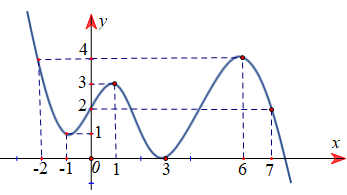
Số nghiệm của phương trình $\mathrm{f}\left(3\mathrm{sinx}\right)=3\left|\mathrm{cosx}\right|$ trên $\left(0;\frac{9\mathrm{\pi }}{2}\right)$ là

A. 16

B. 17

C. 15

D. 18

Đề thi Giữa học kì 2 Toán lớp 12 có đáp án - đề số 3

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa học kì 2

Năm học ...

Môn: Toán 12

Thời gian làm bài: 90 phút

Câu 1: Cho $\mathrm{I}=\underset{1}{\overset{2}{\int }}\mathrm{x}\sqrt{4-{\mathrm{x}}^2}\mathrm{dx}$ và đặt $\mathrm{t}=\sqrt{4-{\mathrm{x}}^2}$. Khẳng định nào sau đây sai?

A. $\mathrm{I}=\sqrt{3}$

B. $\mathrm{I}=\frac{{\mathrm{t}}^2}{2}\left|\begin{array}{l}{}^{\sqrt{3}}\\ {}_0\end{array}\right.$

C. $\mathrm{I}=\underset{0}{\overset{\sqrt{3}}{\int }}{\mathrm{t}}^2\mathrm{dt}$

D. $\mathrm{I}=\frac{{\mathrm{t}}^2}{3}\left|\begin{array}{l}{}^{\sqrt{3}}\\ {}_0\end{array}\right.$

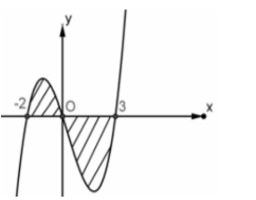
Câu 2: Cho (H) là hình phẳng giới hạn bởi đường cong có phương trình $\mathrm{y}=\sqrt{\mathrm{x}}$, nửa đường tròn có phương trình $\mathrm{y}=\sqrt{2-{\mathrm{x}}^2}$ (với 0 ≤ x ≤ $\sqrt{2}$) và trục hoành (phần tô đậm trong hình vẽ).

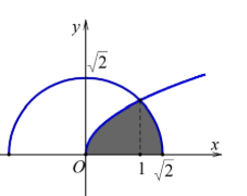
Diện tích của hình (H) bằng:

A. $\frac{3\mathrm{\pi }+2}{12}$

B. $\frac{4\mathrm{\pi }+2}{12}$

C. $\frac{3\mathrm{\pi }+1}{12}$

D. $\frac{4\mathrm{\pi }+1}{6}$

Câu 3: Biết $\int \mathrm{f}\left(\mathrm{u}\right)\mathrm{dy}=\mathrm{F}\left(\mathrm{u}\right)+\mathrm{C}$. Mệnh đề nào dưới đây đúng?

A. $\int \mathrm{f}\left(2\mathrm{x}-1\right)\mathrm{dx}=2\mathrm{F}\left(2\mathrm{x}-1\right)+\mathrm{C}$

B. $\int \mathrm{f}\left(2\mathrm{x}-1\right)\mathrm{dx}=2\mathrm{F}\left(\mathrm{x}\right)-1+\mathrm{C}$

C. $\int \mathrm{f}\left(2\mathrm{x}-1\right)\mathrm{dx}=\frac{1}{2}\mathrm{F}\left(2\mathrm{x}-1\right)+\mathrm{C}$

D. $\int \mathrm{f}\left(2\mathrm{x}-1\right)\mathrm{dx}=\mathrm{F}\left(2\mathrm{x}-1\right)+\mathrm{C}$

Câu 4: Tìm nguyên hàm của hàm số $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{xe}}^{\mathrm{x}}$.

A. $\underset{}{\overset{}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\left(\mathrm{x}+1\right){\mathrm{e}}^{\mathrm{x}}+\mathrm{C}$

B. $\underset{}{\overset{}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\left(\mathrm{x}-1\right){\mathrm{e}}^{\mathrm{x}}+\mathrm{C}$

C. $\underset{}{\overset{}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}={\mathrm{xe}}^{\mathrm{x}}+\mathrm{C}$

D. $\underset{}{\overset{}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}={\mathrm{x}}^2{\mathrm{e}}^{\mathrm{x}}+\mathrm{C}$

Câu 5: Cho hai mặt phẳng (P): x + my + (m – 1)z + 1 = 0 và (Q): x + y + 2z = 0. Tập hợp tất cả các giá trị của m để hai mặt phẳng này không song song là:

A. (0; +∞)

B. R \ {– 1; 1; 2}

C. (–∞;  –3)

D. R

Câu 6: Giả sử $\underset{0}{\overset{9}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=37$ và $\underset{9}{\overset{0}{\int }}\mathrm{g}\left(\mathrm{x}\right)\mathrm{dx}=16$ . Khi đó $\mathrm{I}=\underset{0}{\overset{9}{\int }}\left[2\mathrm{f}\left(\mathrm{x}\right)+3\mathrm{g}\left(\mathrm{x}\right)\right]\mathrm{dx}$ bằng:

A. I = 122

B. I = 26

C. I = 143

D. I = 58

Câu 7: Trong không gian Oxyz, cho ba điểm A(1; – 2; 3), B(4; 2; 3), C(3; 4; 3). Gọi (S₁), (S₂), (S₃) là các mặt cầu có tâm A, B, C và bán kính lần lượt bằng 3, 2, 3. Hỏi có bao nhiêu mặt phẳng qua điểm $\mathrm{I}\left(\frac{14}{5};\frac{2}{5};3\right)$ và tiếp xúc với cả 3 mặt cầu (S₁), (S₂), (S₃).

A. 2

B. 7

C. 0

D. 1

Câu 8: Biết rằng tích phân $\underset{0}{\overset{1}{\int }}\left(2\mathrm{x}+1\right){\mathrm{e}}^{\mathrm{x}}\mathrm{dx}=\mathrm{a}+\mathrm{be}$ với $\mathrm{a}, \mathrm{b}\in \mathrm{ℝ}$, tích ab bằng:

A. 1

B. –1

C. –15

D. 20

Câu 9: Trong không gian với hệ tọa độ Oxyz, cho H(1; 2; 3). Viết phương trình mặt phẳng (P) đi qua điểm H và cắt các trục tọa độ tại ba điểm phân biệt A, B, C sao cho H là trực tâm tam giác ABC.

A. (P): $\mathrm{x}+\frac{\mathrm{y}}{2}+\frac{\mathrm{z}}{3}=1$

B. (P): $\mathrm{x}+2\mathrm{y}+3\mathrm{z}-14=0$

C. (P): x + y + z – 6 = 0

D. (P): $\frac{\mathrm{x}}{3}+\frac{\mathrm{y}}{6}+\frac{\mathrm{z}}{9}=1$

Câu 10: Trong không gian Oxyz, cho hai mặt phẳng (P): x – y – z + 6 = 0; (Q): 2x + 3y – 2z + 1 = 0. Gọi (S) là mặt cầu có tâm thuộc (Q) và cắt (P) theo giao tuyến là đường tròn có tâm E(-1; 2; 3), bán kính r = 8. Phương trình mặt cầu (S) là:

A. x² + (y + 1)² + (z + 2)² = 64

B. x² + (y – 1)² + (z – 2)² = 67

C. x² + (y – 1)² + (z + 2)² = 3

D. x² + (y + 1)² + (z – 2)² = 64

Câu 11: Cho f(x) là hàm chẵn trên $\mathrm{ℝ}$ thỏa mãn $\underset{-3}{\overset{0}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=2$. Chọn mệnh đề đúng.

A. $\underset{-3}{\overset{3}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=4$

B. $\underset{3}{\overset{0}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=2$

C. $\underset{0}{\overset{3}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=-2$

D. $\underset{-3}{\overset{3}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=2$

Câu 12: Trong không gian với hệ tọa độ Oxyz, trong các điểm cho dưới đây, điểm nào thuộc trục Oy?

A. N(2; 0; 0)

B. Q(0; 3; 2)

C. P(2; 0; 3)

D. M(0; -3; 0)

Câu 13: Người ta làm một chiếc phao như hình vẽ (với bề mặt có được bằng cách quay đường tròn (C) quanh trục d). Biết OI = 30 cm, R = 5 cm. Tính thể tích V của chiếc phao.

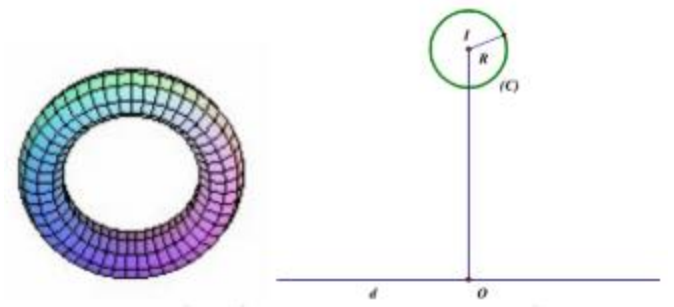
A. V = 1500π² cm³

B. V = 900π² cm³

C. V = 1500π cm³

D. V = 900π cm³

Câu 14: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; -2; 3) và B(5; 4; 7). Phương trình mặt cầu nhận AB làm đường kính là:

A. (x – 6)² + (y – 2)² + (z – 10)² = 17

B. (x – 1)² + (y + 2)² + (z – 3)² = 17

C. (x – 3)² + (y – 1)² + (z – 5)² = 17

D. (x – 5)² + (y – 4)² + (z – 7)² = 17

Câu 15: Tích phân $\mathrm{I}=\underset{1}{\overset{2}{\int }}\left({\mathrm{x}}^2+\frac{\mathrm{x}}{\mathrm{x}+1}\right)\mathrm{dx}$ có giá trị là :

A. $\mathrm{I}=\frac{10}{3}+\ln 2-\ln 3$

B. $\mathrm{I}=\frac{10}{3}+\ln 2+\ln 3$

C. $\mathrm{I}=\frac{10}{3}-\ln 2+\ln 3$

D. $\mathrm{I}=\frac{10}{3}-\ln 2-\ln 3$

Câu 16: Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi đường cong y = f(x), các đường thẳng x = a, x = b là :

A. $\underset{\mathrm{b}}{\overset{\mathrm{a}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

B. $\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

C. $\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)\right|\mathrm{dx}$

D. $-\underset{\mathrm{b}}{\overset{\mathrm{a}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

Câu 17: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(3; 2; -1) và đi qua điểm A(2; 1; 2). Mặt phẳng nào dưới đây tiếp xúc với (S) tại A?

A. x + y – 3z – 8 = 0

B. x + y – 3z + 3 = 0

C. x + y + 3z – 9 = 0

D. x – y – 3z + 3 = 0

Câu 18: Khẳng định nào dưới đây là đúng?

A. $\underset{-2}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=-\underset{0}{\overset{2}{\int }}\left[\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(-\mathrm{x}\right)\right]\mathrm{dx}$

B. $\underset{-2}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=-2\underset{0}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

C. $\underset{-2}{\overset{2}{\int }}2\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=2\underset{-2}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

D. $\underset{-2}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=2\underset{0}{\overset{2}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

Câu 19: Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng (Oxz) là:

A. x = 0

B. x + z = 0

C. z = 0

D. y = 0

Câu 20: Tìm hàm số F(x) biết F'(x) = sin2x và $\mathrm{F}\left(\frac{\mathrm{\pi }}{2}\right)=1$.

A. $\mathrm{F}\left(\mathrm{x}\right)=\frac{1}{2}\cos 2\mathrm{x}+\frac{3}{2}$

B. $\mathrm{F}\left(\mathrm{x}\right)=2\mathrm{x}-\mathrm{\pi }+1$

C. $\mathrm{F}\left(\mathrm{x}\right)=-\frac{1}{2}\cos 2\mathrm{x}+\frac{1}{2}$

D. $\mathrm{F}\left(\mathrm{x}\right)=-\cos 2\mathrm{x}$

Câu 21: Cho đồ thị hàm số y = f(x)  như hình vẽ và $\underset{-2}{\overset{0}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{a},\mathrm{\hspace{0.17em}\hspace{0.17em}}\underset{0}{\overset{3}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{b}$.

Tính diện tích của phần được gạch chéo theo a, b.

A. $\frac{\mathrm{a}+\mathrm{b}}{2}$

B. a – b

C. b – a

D. a + b

Câu 22: Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y = |x|, y = x² – 2.

A. $\mathrm{S}=\frac{20}{3}$

B. $\mathrm{S}=\frac{11}{3}$

C. S = 3

D. $\mathrm{S}=\frac{13}{3}$

Câu 23: Giá trị nào của a để $\underset{0}{\overset{\mathrm{a}}{\int }}\left(3{\mathrm{x}}^2+2\right)\mathrm{dx}={\mathrm{a}}^3+2$?

A. 1

B. 2

C. 0

D. 3

Câu 24: Trong không gian với hệ tọa độ Oxyz, cho A(1; -1; 0), B(0; 2; 0), C(2; 1; 3). Tọa độ điểm M thỏa mãn $\overrightarrow{\mathrm{MA}}-\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}=\overrightarrow{0}$là:

A. (3; 2; -3)

B. (3; -2; 3)

C. (3; - 2; -3)

D. (3; 2; 3)

Câu 25: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x + 3y + 4z – 5 = 0 và điểm A(1; -3; 1). Tính khoảng cách d từ điểm A đến mặt phẳng (P).

A. $\mathrm{d}=\frac{8}{9}$

B. $\mathrm{d}=\frac{8}{29}$

C. $\mathrm{d}=\frac{8}{\sqrt{29}}$

D. $\mathrm{d}=\frac{3}{\sqrt{29}}$

Câu 26: Tìm nguyên hàm của hàm số f(x) = 5^x?

A. $\int \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=5^{\mathrm{x}}\ln 5+\mathrm{C}$

B. $\int \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=5^{\mathrm{x}}+\mathrm{C}$

C. $\int \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\frac{5^{\mathrm{x}}}{\mathrm{lnx}}+\mathrm{C}$

D. $\int \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\frac{5^{\mathrm{x}}}{\ln 5}+\mathrm{C}$

Câu 27: Trong không gian với hệ tọa độ Oxyz, gọi (α) là mặt phẳng cắt ba trục tọa độ tại ba điểm A(4; 0; 0), B(0; -2; 0), C(0; 0; 6). Phương trình mặt phẳng (α) là:

A. $\frac{\mathrm{x}}{4}+\frac{\mathrm{y}}{-2}+\frac{\mathrm{z}}{6}=0$

B. $\frac{\mathrm{x}}{4}+\frac{\mathrm{y}}{-2}+\frac{\mathrm{z}}{6}=-1$

C. $\frac{\mathrm{x}}{4}+\frac{\mathrm{y}}{-2}+\frac{\mathrm{z}}{6}=1$

D. 3x – 6y + 2z – 1 = 0

Câu 28: Hàm số nào dưới đây là nguyên hàm của hàm số $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{\mathrm{x}-1}$ ?

A. $\mathrm{F}\left(\mathrm{x}\right)=-\frac{1}{4}\ln \left|4-4\mathrm{x}\right|+3$

B. $\mathrm{F}\left(\mathrm{x}\right)=-\ln \left|1-\mathrm{x}\right|+4$

C. $\mathrm{F}\left(\mathrm{x}\right)=\ln \left|1-\mathrm{x}\right|+2$

D. $\mathrm{F}\left(\mathrm{x}\right)=\frac{1}{2}\ln \left({\mathrm{x}}^2-2\mathrm{x}+1\right)+5$

Câu 29: Một ô tô đang đi với vận tốc lớn hơn 72km/h, phía trước là đoạn đường chỉ cho phép chạy với tốc độ tối đa là 72km/h, vì thế người lái xe đạp phanh để ô tô chuyển động chậm dần đều với vận tốc v(t) = 30 – 2t (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ 72km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét?

A. 100m

B. 150m

C. 175m

D. 125m

Câu 30: Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị các hàm số y = x² – 2x, y = 0, x = -1, x = 2 quanh quanh trục Ox bằng:

A. $\frac{16\mathrm{\pi }}{5}$

B. $\frac{17\mathrm{\pi }}{5}$

C. $\frac{18\mathrm{\pi }}{5}$

D. $\frac{5\mathrm{\pi }}{18}$

Câu 31: Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi Parabol (P): y = x² và đường thẳng d: y = x xoay quanh trục Ox bằng:

A. $\mathrm{\pi }\underset{0}{\overset{1}{\int }}{\mathrm{x}}^2\mathrm{dx}-\mathrm{\pi }\underset{0}{\overset{1}{\int }}{\mathrm{x}}^4\mathrm{dx}$

B. $\mathrm{\pi }\underset{0}{\overset{1}{\int }}{\mathrm{x}}^2\mathrm{dx}+\mathrm{\pi }\underset{0}{\overset{1}{\int }}{\mathrm{x}}^4\mathrm{dx}$

C. $\mathrm{\pi }\underset{0}{\overset{1}{\int }}{\left({\mathrm{x}}^2-\mathrm{x}\right)}^2\mathrm{dx}$

D. $\mathrm{\pi }\underset{0}{\overset{1}{\int }}\left({\mathrm{x}}^2-\mathrm{x}\right)\mathrm{dx}$

Câu 32: Trong không gian với hệ tọa độ Oxyz, cho A(1; 2; 3), B(-2; 4; 4), C(4; 0; 5). Gọi G là trọng tâm tam giác ABC. Biết điểm M nằm trên mặt phẳng (Oxy) sao cho độ dài đoạn thẳng GM ngắn nhất. Tính độ dài đoạn thẳng GM.

A. GM = 4

B. GM = $\sqrt{5}$

C. GM = 1

D. GM = $\sqrt{2}$

Câu 33: Trong không gian với hệ tọa độ Oxyz, cho điểm $\mathrm{M}(2;-1;1)$.Tìm tọa độ điểm M' là hình chiếu vuông góc của M trên mặt phẳng (Oxy).

A. $\mathrm{M}\text{'}(2;-1;0)$

B. $\mathrm{M}\text{'}(0;0;1)$

C. $\mathrm{M}\text{'}(-2;1;0)$

D. $\mathrm{M}\text{'}(2;1;-1)$

Câu 34: Tìm tập xác định của hàm số $\mathrm{y}={\left(2-\sqrt{\mathrm{x}-1}\right)}^{\sqrt{3}}.$

A. $\mathrm{D}=\left(-\infty ;5\right)$

B. $\mathrm{D}=\left[1;5\right)$

C. $\mathrm{D}=\left(1;3\right]$

D. $\mathrm{D}=\left[1;3\right)$

Câu 35: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB và B’C’. Mặt phẳng (A’MN) cắt cạnh BC tại P.

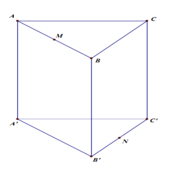
Thể tích khối đa diện MBP.A’B’N’ là:

A. $\frac{\sqrt{3}{\mathrm{a}}^3}{24}$

B. $\frac{7\sqrt{3}{\mathrm{a}}^3}{96}$

C. $\frac{\sqrt{3}{\mathrm{a}}^3}{12}$

D. $\frac{7\sqrt{3}{\mathrm{a}}^3}{32}$

Câu 36: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có phương trình đường phân giác góc A là $\frac{\mathrm{x}}{1}=\frac{\mathrm{y}-6}{-4}=\frac{\mathrm{z}-6}{-3}.$ Biết rằng điểm $\mathrm{M}(0;5;3)$ thuộc đường thẳng AB và điểm $\mathrm{N}(1;1;0)$ thuộc đường thẳng AC. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng AC ?

A. $\overrightarrow{\mathrm{u}}(1;2;3)$

B. $\overrightarrow{\mathrm{u}}(0;-2;6)$

C. $\overrightarrow{\mathrm{u}}(0;1;-3)$

D. $\overrightarrow{\mathrm{u}}(0;1;3)$

Câu 37: Cần phải làm cái cửa sổ mà phía trên là hình bán nguyệt, phía dưới là hình chữ nhật, có chu vi là a mét (a chính là chu vi hình bán nguyệt cộng với chu vi hình chữ nhật trừ đi đường kính của hình bán nguyệt). Gọi d là đường kính của hình bán nguyệt.

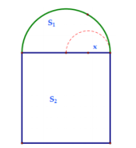
Hãy xác định d để diện tích cửa sổ là lớn
nhất.

A. $\mathrm{d}=\frac{\mathrm{a}}{4+\mathrm{\pi }}$

B. $\mathrm{d}=\frac{2\mathrm{a}}{4+\mathrm{\pi }}$

C. $\mathrm{d}=\frac{\mathrm{a}}{2+\mathrm{\pi }}$

D. $\mathrm{d}=\frac{2\mathrm{a}}{2+\mathrm{\pi }}$

Câu 38: Trong không gian với hệ tọa độ Oxyz, cho 3 điểm $\mathrm{A}(1;2;-1),\mathrm{B}(-3;4;3),\mathrm{C}(3;1;-3)$. Số điểm D sao cho 4 điểm A, B, C, D là 4 đỉnh của một hình bình hành là:

A. 3

B. 1

C. 1

D. 0

Câu 39: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $\left(\mathrm{S}\right):\mathrm{x}{}_2+{\mathrm{y}}^2+{\mathrm{z}}^2-2(\mathrm{x}+2\mathrm{y}+3\mathrm{z})=0.$ Gọi A, B, C lần lượt là giao điểm (khác gốc tọa độ O) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là:

A. $6\mathrm{x}-3\mathrm{y}-2\mathrm{z}-12=0$

B. $6\mathrm{x}+3\mathrm{y}+2\mathrm{z}-12=0$

C. $6\mathrm{x}-3\mathrm{y}-2\mathrm{z}+12=0$

D. $6\mathrm{x}-3\mathrm{y}+2\mathrm{z}-12=0$

Câu 40: Khoảng cách giữa hai tiệm cận đứng của đồ thị hàm số $\mathrm{y}=\frac{1}{{\mathrm{x}}^2-2}$ bằng:

A. 2

B. $\sqrt{2}$

C. $2\sqrt{2}$

D. 4

Câu 41: Diện tích của hình phẳng (H) được giới hạn bởi đồ thị hàm số $\mathrm{y}=\mathrm{f}\left(\mathrm{x}\right)$, trục hoành và hai đường $\mathrm{x}=\mathrm{a},\mathrm{x}=\mathrm{b},(\mathrm{a}<\mathrm{b})$ (phần tô đậm trong hình vẽ) tính theo công thức:

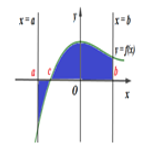
A. $\mathrm{S}=\underset{\mathrm{a}}{\overset{\mathrm{c}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}+\underset{\mathrm{c}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

B. $\mathrm{S}=\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

C. $\mathrm{S}=\left|\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\right|$

D. $\mathrm{S}=-\underset{\mathrm{a}}{\overset{\mathrm{c}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}+\underset{\mathrm{c}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

Câu 42: Trong mặt phẳng tọa độ Oxy, gọi (H) là phần mặt phẳng chứa các điểm biểu diễn các số phức z thỏa mãn $\frac{\mathrm{z}}{16}$ và $\frac{16}{\overline{\mathrm{z}}}$ có phần thực và phần ảo đều thuộc đoạn $\left[0;1\right].$ Tính diện tích S của (H).

A. $\mathrm{S}=256$

B. $\mathrm{S}=64\mathrm{\pi }$

C. $\mathrm{S}=16(4-\mathrm{\pi })$

D. $\mathrm{S}=32(6-\mathrm{\pi })$

Câu 43: Biết tích phân $\underset{0}{\overset{\ln 6}{\int }}\frac{{\mathrm{e}}^{\mathrm{x}}}{1+\sqrt{{\mathrm{e}}^{\mathrm{x}}+3}}\mathrm{dx}=\mathrm{a}+\mathrm{bln}2+\mathrm{cln}3$ với a, b, c là các số nguyên dương. Tính T = a + b + c.

A.T = 2

B. T = 1

C. T = 0

D.T = -1

Câu 44: Cho hàm số $\mathrm{y}=\mathrm{f}\left(\mathrm{x}\right)$ có đạo hàm liên tục trên đoạn $\left[0;\frac{\mathrm{\pi }}{4}\right]$ và $\mathrm{f}\left(\frac{\mathrm{\pi }}{4}\right)=0.$ Biết $\underset{0}{\overset{\frac{\mathrm{\pi }}{4}}{\int }}{\mathrm{f}}^2\left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{\pi }}{8},\underset{0}{\overset{\frac{\mathrm{\pi }}{4}}{\int }}{\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right)\sin 2\mathrm{xdx}=-\frac{\mathrm{\pi }}{4}.$ Tính tích phân $\mathrm{I}=\underset{0}{\overset{\frac{\mathrm{\pi }}{8}}{\int }}\mathrm{f}\left(2\mathrm{x}\right)\mathrm{dx}.$

A. $\mathrm{I}=\frac{1}{2}$

B. $\mathrm{I}=\frac{1}{4}$

C. I = 2

D. I = 1

Câu 45: Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật. $\mathrm{AB}=\mathrm{a}, \mathrm{AD}=\mathrm{a}\sqrt{3}$. Hình chiếu vuông góc của điểm A’ trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B’ đến (A’BD) .

A. $\frac{\mathrm{a}\sqrt{3}}{3}$

B. $\frac{\mathrm{a}\sqrt{3}}{4}$

C. $\frac{\mathrm{a}\sqrt{3}}{2}$

D. $\frac{\mathrm{a}\sqrt{3}}{6}$

Câu 46: Giải bóng chuyền VTV Cup gồm 12 đội tham dự trong đó có 9 đội bóng nước ngoài, 3 đội bóng của Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia 3 bảng A, B, C mỗi bảng 4 đội. Tính xác suất để ba đội Việt Nam ở 3 bảng khác nhau.

A. $\frac{16}{55}$

B. $\frac{133}{165}$

C. $\frac{32}{165}$

D. $\frac{39}{65}$

Câu 47: Hình nón đỉnh S, đáy là hình tròn nội tiếp tam giác ABC. Biết rằng AB = BC = 10a, AC = 12a, góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng 45°. Tính thể tích V của khối nón đã cho.

A. $\mathrm{V}=9{\mathrm{\pi a}}^3$

B. $\mathrm{V}=12{\mathrm{\pi a}}^3$

C. $\mathrm{V}=27{\mathrm{\pi a}}^3$

D. $\mathrm{V}=3{\mathrm{\pi a}}^3$

Câu 48: Tìm tập hợp tất cả các giá trị thực của m để phương trình $1+{\log }_5({\mathrm{x}}^2+1)={\log }_5({\mathrm{mx}}^2+4\mathrm{x}+\mathrm{m})$ có hai nghiệm phân biệt.

A. $\mathrm{m}\in (3;7) \backslash \left\{5\right\}$

B. $\mathrm{m}\in (3;7)$

C. $\mathrm{m}\in \mathrm{ℝ} \backslash \left\{5\right\}$

D. $\mathrm{m}\in \mathrm{ℝ}$

Câu 49: Cho hàm số y = f(x) liên tục trên [1; 4] và thỏa mãn $\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{f}(2\sqrt{\mathrm{x}}-1)}{\sqrt{\mathrm{x}}}+\frac{\mathrm{lnx}}{\mathrm{x}}.$ Tính tích phân $\mathrm{I}=\underset{3}{\overset{4}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}.$

A. $\mathrm{I}=2{\ln }^{2}2$

B. $\mathrm{I}=2\ln 2$

C. $\mathrm{I}=3+2{\ln }^{2}2$

D. $\mathrm{I}={\ln }^{2}2$

Câu 50: Trong không gian với hệ tọa độ Oxyz, cho điểm $\mathrm{A}(1;2;-3)$ và mặt phẳng $\left(\mathrm{P}\right):2\mathrm{x}+2\mathrm{y}-\mathrm{z}+9=0.$ Đường thẳng đi qua A và vuông góc với mặt phẳng $\left(\mathrm{Q}\right):3\mathrm{x}+4\mathrm{y}-4\mathrm{z}+5=0$ cắt mặt phẳng (P) tại B. Điểm M nằm trong mặt phẳng (P) luôn nhìn đoạn AB dưới một góc vuông và độ dài MB lớn nhất. Tính độ dài MB.

A. $\mathrm{MB}=\sqrt{5}$

B. $\mathrm{MB}=\frac{\sqrt{5}}{2}$

C. $\mathrm{MB}=\frac{\sqrt{41}}{2}$

D. $\mathrm{MB}=\sqrt{41}$

Đề thi Giữa học kì 2 Toán lớp 12 - đề số 4

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa học kì 2

Năm học ...

Môn: Toán 12

Thời gian làm bài: 90 phút

Câu 1: Trong không gian với hệ tọa độ Oxyz, cho điểm H(1; 2; 3). Viết phương trình mặt phẳng (P) đi qua H, cắt các trục $\mathrm{x}\text{'}\mathrm{Ox},\mathrm{y}\text{'}\mathrm{Oy},\mathrm{z}\text{'}\mathrm{Oz}$ lần lượt tại các điểm A, B, C $\left(\mathrm{A},\mathrm{B},\mathrm{C}\ne \mathrm{O}\right)$ sao cho H là trực tâm của tam giác ABC.

A. $\left(\mathrm{P}\right):2\mathrm{x}+\mathrm{y}+3\mathrm{z}-13=0$

B. $\left(\mathrm{P}\right):2\mathrm{x}+3\mathrm{y}+\mathrm{z}-11=0$

C. $\left(\mathrm{P}\right):\mathrm{x}+2\mathrm{y}+3\mathrm{z}-14=0$

D. $\left(\mathrm{P}\right):\mathrm{x}+3\mathrm{y}+2\mathrm{z}-13=0$

Câu 2: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $\left(\mathrm{S}\right):{\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2-2\mathrm{x}-2\mathrm{y}-2\mathrm{z}=0$ và điểm A(2; 2; 0). Viết phương trình mặt phẳng (OAB), biết rằng điểm B thuộc mặt cầu (S), có hoành độ dương và tam giác OAB đều.

A. $\mathrm{x}-\mathrm{y}-2\mathrm{z}=0$

B. $\mathrm{x}-\mathrm{y}+\mathrm{z}=0$

C. $\mathrm{x}-\mathrm{y}-\mathrm{z}=0$

D. $\mathrm{x}-\mathrm{y}+2\mathrm{z}=0$

Câu 3: Cho hai số phức z₁ = 7 + 9i và z₂ = 8i. Gọi $\mathrm{z}=\mathrm{a}+\mathrm{bi}\mathrm{ }\left(\mathrm{a},\mathrm{b}\in \mathrm{ℝ}\right)$ là số phức thỏa mãn $\left|\mathrm{z}-1-\mathrm{i}\right|=5$. Tìm a + b, biết biểu thức $\mathrm{P}=\left|\mathrm{z}-{\mathrm{z}}_1\right|+2\left|\mathrm{z}-{\mathrm{z}}_2\right|$ đạt giá trị nhỏ nhất.

A. ‒3

B. ‒7

C. 3

D. 7

Câu 4: Trong không gian với hệ tọa độ Oxyz, cho hình lăng trụ đứng $\mathrm{ABC}.\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}$ có $\mathrm{A}\left({\mathrm{x}}_0;0;0\right)$, $\mathrm{B}\left(-{\mathrm{x}}_0;0;0\right)$, $\mathrm{C}\left(0;1;0\right)$ và $\mathrm{B}\text{'}\left(-{\mathrm{x}}_0;0;{\mathrm{y}}_0\right)$, trong đó  ${\mathrm{x}}_0; {\mathrm{y}}_0$ là các số thực dương và thỏa mãn ${\mathrm{x}}_0+{\mathrm{y}}_0=4$. Khi khoảng cách giữa hai đường thẳng $\mathrm{AC}\text{'}$ và $\mathrm{B}\text{'}\mathrm{C}$ lớn nhất thì mặt cầu ngoại tiếp hình lăng trụ có bán kính R bằng bao nhiêu?

A. $\mathrm{R}=\sqrt{17}$

B. $\mathrm{R}=\frac{29}{4}$

C. R = 17

D. $\mathrm{R}=\frac{\sqrt{29}}{2}$

Câu 5: Họ nguyên hàm của hàm số $\int \frac{\mathrm{dx}}{\sqrt{2\mathrm{x}-1}+4}$ là

A. $\sqrt{2\mathrm{x}-1}-2\ln \left(\sqrt{2\mathrm{x}-1}+4\right)+\mathrm{C}$

B. $\sqrt{2\mathrm{x}-1}-\ln \left(\sqrt{2\mathrm{x}-1}+4\right)+\mathrm{C}$

C. $\sqrt{2\mathrm{x}-1}-4\ln \left(\sqrt{2\mathrm{x}-1}+4\right)+\mathrm{C}$

D. $2\sqrt{2\mathrm{x}-1}-\ln \left(\sqrt{2\mathrm{x}-1}+4\right)+\mathrm{C}$

Câu 6: Tính tích phân $\underset{1}{\overset{\mathrm{e}}{\int }}{\mathrm{x}}^2\mathrm{lnxdx}$

A. $\frac{2{\mathrm{e}}^3+1}{9}$

B. $\frac{2{\mathrm{e}}^3-1}{9}$

C. $\frac{{\mathrm{e}}^3-2}{9}$

D. $\frac{{\mathrm{e}}^3+2}{9}$

Câu 7: Căn bậc hai của số phức z = -25 là

A. ${\mathrm{x}}_{1,2}=\pm 5$

B. Không tồn tại

C. ${\mathrm{x}}_{1,2}=\pm 25\mathrm{i}$

D. ${\mathrm{x}}_{1,2}=\pm 5\mathrm{i}$

Câu 8: Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng ${\mathrm{\Delta }}_1:\left\{\begin{array}{l}\mathrm{x}=-3+2\mathrm{t}\\ \mathrm{y}=1-\mathrm{t}\\ \mathrm{z}=-1+4\mathrm{t}\end{array}\right.$ và ${\mathrm{\Delta }}_2:\frac{\mathrm{x}+4}{3}=\frac{\mathrm{y}+2}{2}=\frac{\mathrm{z}-4}{-1}$. Khẳng định nào sau đây đúng?

A. ${\mathrm{\Delta }}_1,{\mathrm{\Delta }}_2$ chéo nhau và vuông góc nhau

B. ${\mathrm{\Delta }}_1$ cắt và không vuông góc với ${\mathrm{\Delta }}_2$

C. ${\mathrm{\Delta }}_1$ cắt và vuông góc với ${\mathrm{\Delta }}_2$

D. ${\mathrm{\Delta }}_1$ và ${\mathrm{\Delta }}_2$ song song với nhau

Câu 9: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $\left(\mathrm{P}\right):3\mathrm{x}+2\mathrm{y}-\mathrm{z}+1=0$. Mặt phẳng (P) có vectơ pháp tuyến là

A. $\overrightarrow{\mathrm{n}}=\left(-1;3;2\right)$

B. $\overrightarrow{\mathrm{n}}=\left(3;-1;2\right)$

C. $\overrightarrow{\mathrm{n}}=\left(2;3;-1\right)$

D. $\overrightarrow{\mathrm{n}}=\left(3;2;-1\right)$

Câu 10: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $\left(\mathrm{S}\right):{\left(\mathrm{x}-2\right)}^2+{\mathrm{y}}^2+{\left(\mathrm{z}+1\right)}^2=9$. Tọa độ tâm I của mặt cầu (S) là

A. $\mathrm{I}\left(2;-1;3\right)$

B. $\mathrm{I}\left(2;0;-1\right)$

C. $\mathrm{I}\left(-2;0;1\right)$

D. $\mathrm{I}\left(2;-1;0\right)$

Câu 11: Cho số phức z = 1 – 2i. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức liên hợp của số phức z?

A. ${\mathrm{M}}_1\left(1;2\right)$

B. ${\mathrm{M}}_2\left(-1;2\right)$

C. ${\mathrm{M}}_3\left(-1;-2\right)$

D. ${\mathrm{M}}_4\left(1;-2\right)$

Câu 12: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có $\mathrm{A}\left(2;-1;3\right), \mathrm{B}\left(3;5;-1\right)$ và C(1; 2; 7). Tìm tọa độ trọng tâm G của tam giác ABC.

A. $\mathrm{G}\left(2;2;3\right)$

B. $\mathrm{G}\left(6;6;9\right)$

C. $\mathrm{G}\left(\frac{4}{3};\frac{7}{3};\frac{10}{3}\right)$

D. $\mathrm{G}\left(3;3;\frac{9}{2}\right)$

Câu 13: Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD với $\mathrm{A}\left(0;0;3\right), \mathrm{B}\left(0;0;-1\right), \mathrm{C}\left(1;0;-1\right)$ và $\mathrm{D}\left(0;1;-1\right)$. Mệnh đề nào dưới đây sai?

A. $\mathrm{AB}\perp \mathrm{BC}$

B. $\mathrm{AB}\perp \mathrm{BD}$

C. $\mathrm{AB}\perp \mathrm{CD}$

D. $\mathrm{AB}\perp \mathrm{AC}$

Câu 14: Trong mặt phẳng tọa độ xét ba điểm A, B, C theo thứ tự biểu diễn ba số phức z₁, z₂, z₃ thỏa mãn $\left|{\mathrm{z}}_1\right|=\left|{\mathrm{z}}_2\right|=\left|{\mathrm{z}}_3\right|$ và z₁ + z₂ + z₃ = 0. Hỏi tam giác ABC là tam giác gì?

A. Tam giác vuông cân

B. Tam giác vuông có một góc nhọn bằng 30°

C. Tam giác đều

D. Tam giác cân có góc ở đỉnh bằng 30°

Câu 15: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3) và mặt phẳng $\left(\mathrm{\alpha }\right):\mathrm{x}-4\mathrm{y}+\mathrm{z}=0$. Viết phương trình mặt phẳng (β) đi qua A và song song với mặt phẳng (α).

A. $\mathrm{x}-4\mathrm{y}+\mathrm{z}-4=0$

B. $\mathrm{x}-4\mathrm{y}+\mathrm{z}+4=0$

C. $2\mathrm{x}+\mathrm{y}+2\mathrm{z}-10=0$

D. $2\mathrm{x}+\mathrm{y}+2\mathrm{z}+10=0$

Câu 16: Cho phương trình ${\mathrm{z}}^4+2{\mathrm{z}}^2-8=0$ có các nghiệm là z₁, z₂, z₃, z₄. Tính giá trị biểu thức $\mathrm{F}={\mathrm{z}}_1^2+{\mathrm{z}}_2^2+{\mathrm{z}}_3^2+{\mathrm{z}}_4^2$.

A. F = 4

B. F = - 4

C. F = 2

D. F = -2

Câu 17: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $\mathrm{d}:\frac{\mathrm{x}+1}{2}=\frac{\mathrm{y}}{1}=\frac{\mathrm{z}-2}{1}$, mặt phẳng $\left(\mathrm{P}\right):\mathrm{x}+\mathrm{y}-2\mathrm{z}+5=0$ và điểm $\mathrm{A}\left(1;-1;2\right)$. Viết phương trình đường thẳng ∆ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN.

A. $\mathrm{\Delta }:\frac{\mathrm{x}-3}{2}=\frac{\mathrm{y}-2}{3}=\frac{\mathrm{z}-4}{2}$

B. $\mathrm{\Delta }:\frac{\mathrm{x}-1}{6}=\frac{\mathrm{y}+1}{1}=\frac{\mathrm{z}-2}{2}$

C. $\mathrm{\Delta }:\frac{\mathrm{x}+5}{6}=\frac{\mathrm{y}+2}{1}=\frac{\mathrm{z}}{2}$

D. $\mathrm{\Delta }:\frac{\mathrm{x}+1}{2}=\frac{\mathrm{y}+4}{3}=\frac{\mathrm{z}-3}{2}$

Câu 18: Cho số phức $\mathrm{z}=\mathrm{a}+\mathrm{bi},\left(\mathrm{a},\mathrm{b}\in \mathrm{ℝ}\right)$; ${\mathrm{a}}^2+{\mathrm{b}}^2>0$ thỏa mãn $\left(1-\mathrm{i}\right){\left|\mathrm{z}\right|}^2+\left(2+2\mathrm{i}\right){\mathrm{z}}^2+2\mathrm{z}\left(\mathrm{z}+\mathrm{i}\right)=0$. Tìm giá trị của biểu thức $\mathrm{F}=\frac{\mathrm{a}}{\mathrm{b}}$.

A. $\mathrm{F}=-5$

B. $\mathrm{F}=-\frac{1}{5}$

C. $\mathrm{F}=\frac{3}{5}$

D. $\mathrm{F}=\frac{5}{3}$

Câu 19: Cho hai số thực a và b (a < b) sao cho ${\int }_{\mathrm{a}}^{\mathrm{b}}\left(3+2\mathrm{x}-{\mathrm{x}}^2\right)\mathrm{dx}$ đạt giá trị lớn nhất. Tìm b – a.

A. 2

B. 4

C. 6

D. 8

Câu 20: Gọi h(t) (cm) là mức nước ở một bồn chứa sau khi bơm nước vào bồn được t giây. Biết rằng $\mathrm{h}\text{'}\left(\mathrm{t}\right)=\frac{1}{5}\sqrt[3]{\mathrm{t}+8}$ và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 56 giây.

A. 40,8 cm

B. 38,4 cm

C. 36 cm

D. 51,2 cm

Câu 21: Công thức tính diện tích S của hình phẳng giới hạn bởi các đồ thị hàm số y = f(x), y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a,  x = b với a < b là

A. $\mathrm{S}=\left|\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\right|+\left|\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\mathrm{g}\left(\mathrm{x}\right)\mathrm{dx}\right|$

B. $\mathrm{S}=\left|\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\left[\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right]\mathrm{dx}\right|$

C. $\mathrm{S}=\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{dx}$

D. $\mathrm{S}=\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)\right|\mathrm{dx}+\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{dx}$

Câu 22: Biết phương trình ${\mathrm{z}}^2+\mathrm{az}+\mathrm{b}=0$, $\left(\mathrm{a},\mathrm{b}\in \mathrm{ℝ}\right)$ có một nghiệm phức là ${\mathrm{z}}_0=1+2\mathrm{i}$. Tìm a, b

A. $\left[\begin{array}{l}\mathrm{a}=-2\\ \mathrm{b}=5\end{array}\right.$

B. $\left[\begin{array}{l}\mathrm{a}=5\\ \mathrm{b}=-2\end{array}\right.$

C. $\left\{\begin{array}{l}\mathrm{a}=5\\ \mathrm{b}=-2\end{array}\right.$

D. $\left\{\begin{array}{l}\mathrm{a}=-2\\ \mathrm{b}=5\end{array}\right.$  

Câu 23: Trong không gian với hệ trục tọa độ Oxyz, cho điểm $\mathrm{A}\left(4;1;-2\right)$. Tọa độ điểm đối xứng với A qua mặt phẳng (Oxz) là

A. $\mathrm{A}\text{'}\left(4;-1;2\right)$

B. $\mathrm{A}\text{'}\left(-4;-1;2\right)$

C. $\mathrm{A}\text{'}\left(4;-1;-2\right)$

D. $\mathrm{A}\text{'}\left(4;1;2\right)$

Câu 24: Cho hàm số $\mathrm{y}={\mathrm{ax}}^4+{\mathrm{bx}}^2+\mathrm{c}$ có đồ thị (C), biết rằng (C) đi qua điểm $\mathrm{A}\left(-1;0\right)$. Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0, x = 2 bằng $\frac{28}{5}$ (phần tô đậm trong hình vẽ).

Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = -1, x = 0 có diện tích bằng

A. $\frac{2}{5}$

B. $\frac{1}{9}$

C. $\frac{2}{9}$

D. $\frac{1}{5}$

Câu 25: Chất điểm chuyển động theo một đường thẳng sau t giây đạt được vận tốc $\mathrm{v}={\mathrm{t}}^2.{\mathrm{e}}^{-5}$ (m/s). Tính quãng đường nó đi được trong t giây đầu tiên

A. $\mathrm{S}\left(\mathrm{t}\right)=2-{\mathrm{e}}^{-3\mathrm{t}}\left({\mathrm{t}}^2+2\mathrm{t}\right)$

B. $\mathrm{S}\left(\mathrm{t}\right)=2-{\mathrm{e}}^{-\mathrm{t}}\left({\mathrm{t}}^2+2\mathrm{t}+2\right)$

C. $\mathrm{S}\left(\mathrm{t}\right)=2-{\mathrm{e}}^{-\mathrm{t}}\left({\mathrm{t}}^2+3\mathrm{t}+2\right)$

D. $\mathrm{S}\left(\mathrm{t}\right)=1-{\mathrm{e}}^{-\mathrm{t}}\left(5{\mathrm{t}}^2+2\mathrm{t}+2\right)$

Câu 26: Cho hình phẳng D giới hạn bởi parabol $\left(\mathrm{P}\right):\mathrm{y}=2\mathrm{x}-{\mathrm{x}}^2$ và trục hoành Ox: y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình phẳng D quanh trục Oy

A. ${\mathrm{V}}_{\mathrm{y}}=\frac{4\mathrm{\pi }}{3}$

B. ${\mathrm{V}}_{\mathrm{y}}=\frac{\mathrm{\pi }}{3}$

C. ${\mathrm{V}}_{\mathrm{y}}=\frac{8\mathrm{\pi }}{3}$

D. ${\mathrm{V}}_{\mathrm{y}}=\frac{2\mathrm{\pi }}{3}$

Câu 27: Cho hai số phức z₁, z₂ thỏa mãn $\left|{\mathrm{z}}_1\right|=3, \left|{\mathrm{z}}_2\right|=4, \left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|=\sqrt{37}$. Xét số phức $\mathrm{z}=\frac{{\mathrm{z}}_1}{{\mathrm{z}}_2}=\mathrm{a}+\mathrm{bi}$. Tìm $\left|\mathrm{b}\right|$

A. $\left|\mathrm{b}\right|=\frac{3\sqrt{3}}{8}$

B. $\left|\mathrm{b}\right|=\frac{\sqrt{39}}{8}$

C. $\left|\mathrm{b}\right|=\frac{3}{8}$

D. $\left|\mathrm{b}\right|=\frac{\sqrt{3}}{8}$

Câu 28: Trong không gian với hệ tọa độ Oxyz, biết rằng tập hợp các điểm M(x, y, z) sao cho |x| + |y| + |z| = 3 là một hình đa diện. Tính thể tích V của khối đa diện đó

A. V = 54

B. V = 72

C. V = 36

D. V = 27

Câu 29: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) và mặt phẳng (P) có phương trình lần lượt là $\left(\mathrm{S}\right):{\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2-2\mathrm{x}+4\mathrm{y}-6\mathrm{z}-11=0$ và $\left(\mathrm{P}\right):2\mathrm{x}+2\mathrm{y}-\mathrm{z}+17=0$. Viết phương trình mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) theo một giao tuyến là đường tròn có chu vi bằng $6\mathrm{\pi }$

A. $\left(\mathrm{Q}\right):2\mathrm{x}+2\mathrm{y}-\mathrm{z}=0$

B. $\left(\mathrm{Q}\right):2\mathrm{x}+2\mathrm{y}-\mathrm{z}+5=0$

C. $\left(\mathrm{Q}\right):2\mathrm{x}+2\mathrm{y}-\mathrm{z}-2=0$

D. $\left(\mathrm{Q}\right):2\mathrm{x}+2\mathrm{y}-\mathrm{z}-7=0$

Câu 30: Cho z₁, z₂, z₃, z₄ là bốn nghiệm của phương trình ${\left(\frac{\mathrm{z}-1}{2\mathrm{z}-\mathrm{i}}\right)}^4=1$. Tính giá trị của biểu thức $\mathrm{P}=\left({\mathrm{z}}_1^2+1\right)\left({\mathrm{z}}_2^2+1\right)\left({\mathrm{z}}_3^2+1\right)\left({\mathrm{z}}_4^2+1\right)$

A. $\mathrm{P}=\frac{17}{9}$

B. $\mathrm{P}=-\frac{17}{9}$

C. $\mathrm{P}=425$

D. $\mathrm{P}=-425$

Câu 31: Trong không gian với hệ tọa độ Oxyz, xét các điểm $\mathrm{A}\left(\mathrm{a};0;0\right), \mathrm{B}\left(0;\mathrm{b};0\right), \mathrm{C}\left(0;0;\mathrm{c}\right)$ với a, b, c khác 0 và a + 2b + 2c = 6. Biết rằng khi a, b, c thay đổi thì quỹ tích tâm mặt cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ điểm O đến mặt phẳng (P)

A. d = 1

B. $\mathrm{d}=\sqrt{3}$

C. d = 2

D. d = 3

Câu 32: Cho hàm số y = f(x) liên tục và không âm trên $\mathrm{ℝ}$ thỏa mãn $\mathrm{f}\left(\mathrm{x}\right).\mathrm{f}\text{'}\left(\mathrm{x}\right)=2\mathrm{x}\sqrt{{\mathrm{f}}^2\left(\mathrm{x}\right)+1}$ và f(0) = 0. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1; 3]. Biết rằng giá trị của biểu thức P = 2M – m có dạng $\mathrm{a}\sqrt{11}-\mathrm{b}\sqrt{3}+\mathrm{c}$, $\left(\mathrm{a},\mathrm{b},\mathrm{c}\in \mathrm{\mathbb{Z}}\right)$. Tính a + b + c.

A. a + b + c = 4

B. a + b + c = 7

C. a + b + c = 6

D. a + b + c = 5

Câu 33: Biết rằng nghịch đảo của số phức $\mathrm{z}\left(\mathrm{z}\ne \pm 1\right)$ bằng số phức liên hợp của nó. Mệnh đề nào dưới đây đúng?

A. $\mathrm{z}\in \mathrm{ℝ}$

B. z là một số thuần ảo

C. |z| = -1

D. |z| = 1

Câu 34: Biết phương trình $7{\mathrm{z}}^2+3\mathrm{z}+2=0$ có hai nghiệm z₁, z₂ trên tập số phức. Tính giá trị biểu thức $\mathrm{A}={\mathrm{z}}_1^3{\mathrm{z}}_2+{\mathrm{z}}_1{\mathrm{z}}_2^3$

A. $\frac{81}{19208}$

B. $-\frac{38}{343}$

C. $-\frac{74}{343}$

 D. $-\frac{138}{343}$

Câu 35: Trong không gian Oxyz cho hình hộp $\mathrm{ABCD}.\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}\mathrm{D}\text{'}$. Biết $\mathrm{A}=\left(1;0;1\right), \mathrm{B}=\left(2;1;2\right)$, $\mathrm{D}=\left(1;-1;1\right)$ và $\mathrm{C}\text{'}=\left(4;5;-5\right)$. Tìm tọa độ đỉnh D'.

A. $\mathrm{D}\text{'}\left(5;6;-4\right)$

B. $\mathrm{D}\text{'}\left(-1;-6;8\right)$

C. $\mathrm{D}\text{'}\left(-3;-8;6\right)$

D. $\mathrm{D}\text{'}\left(3;4;-6\right)$

Câu 36: Tính diện tích hình phẳng giới hạn bởi đường cong y = x­², tiếp tuyến với đường cong đó tại điểm có hoành độ bằng 2 và trục Oy.

A. $\frac{-40}{3}$

B. $\frac{8}{3}$

C. $\frac{20}{3}$

D. $\frac{68}{3}$

Câu 37: Trong không gian Oxyz cho đường thẳng Δ có phương trình $\frac{\mathrm{x}-2}{1}=\frac{\mathrm{y}+3}{2}=\frac{\mathrm{z}-1}{3}$. Tìm phương trình tham số của đường thẳng d là hình chiếu vuông góc của Δ trên mặt phẳng (Oyz).

A. $\left\{\begin{array}{l}\mathrm{x}=0\\ \mathrm{y}=3+2\mathrm{t}\\ \mathrm{z}=-1+3\mathrm{t}\end{array}\right.$

B. $\left\{\begin{array}{l}\mathrm{x}=0\\ \mathrm{y}=-3+2\mathrm{t}\\ \mathrm{z}=1+3\mathrm{t}\end{array}\right.$

C. $\left\{\begin{array}{l}\mathrm{x}=-2+\mathrm{t}\\ \mathrm{y}=0\\ \mathrm{z}=0\end{array}\right.$

D. $\left\{\begin{array}{l}\mathrm{x}=2+\mathrm{t}\\ \mathrm{y}=0\\ \mathrm{z}=0\end{array}\right.$

Câu 38: Trong không gian Oxyz, viết phương trình mặt phẳng (P) chứa hai đường thẳng $\mathrm{d}:\frac{\mathrm{x}-5}{2}=\frac{\mathrm{y}-1}{-1}=\frac{\mathrm{z}-5}{1}$ và $\mathrm{d}\text{'}:\frac{\mathrm{x}-3}{-2}=\frac{\mathrm{y}+3}{1}=\frac{\mathrm{z}-1}{-1}$.

A. $\left(\mathrm{P}\right):\mathrm{x}-2\mathrm{y}-4\mathrm{z}+17=0$                                

B. $\left(\mathrm{P}\right):2\mathrm{x}+2\mathrm{y}-3\mathrm{z}+3=0$  

C. (P):$4\mathrm{x}-\mathrm{y}-\mathrm{z}-14=0$

D. $\left(\mathrm{P}\right):4\mathrm{x}+3\mathrm{y}-5\mathrm{z}+2=0$  

Câu 39: Tính khoảng cách từ điểm A(1; 2; 1) đến đường thẳng $\mathrm{d}:\frac{\mathrm{x}+2}{1}=\frac{\mathrm{y}-1}{2}=\frac{\mathrm{z}+1}{-2}$.

A. $\frac{5\sqrt{5}}{3}$

B. $\frac{5\sqrt{70}}{14}$

C. $\frac{10\sqrt{5}}{3}$

D. $\frac{5\sqrt{70}}{7}$

Câu 40: Xét hàm số $\mathrm{F}\left(\mathrm{x}\right)={\int }_2^{\mathrm{x}}\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}$ trong đó hàm số y = f(t) có đồ thị như hình vẽ bên.

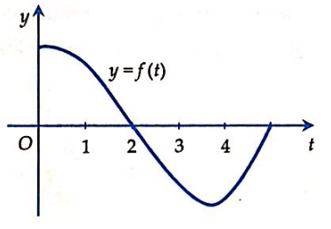
Giá trị nào dưới đây là lớn nhất?

A. F(0)

B. F(1)

C. F(2)

D. F(3)

Câu 41: Biết các số phức z₁, z₂, z₃ được biểu diễn bởi ba đỉnh của một hình bình hành nào đó trong mặt phẳng phức. Trong các số phức sau, tìm số phức được biểu diễn bởi đỉnh còn lại.

A. ${\mathrm{z}}_1+{\mathrm{z}}_2+{\mathrm{z}}_3$

B. ${\mathrm{z}}_1+{\mathrm{z}}_2-{\mathrm{z}}_3$

C. ${\mathrm{z}}_1-{\mathrm{z}}_2-{\mathrm{z}}_3$

D. $-{\mathrm{z}}_1-{\mathrm{z}}_2-{\mathrm{z}}_3$

Câu 42: Trong không gian Oxyz cho ba điểm $\mathrm{A}\left(-1;2;2\right)$, $\mathrm{B}\left(3;-1;-2\right)$ và $\mathrm{C}\left(-4;0;3\right)$. Tìm tọa độ điểm I trên mặt phẳng (Oxz) sao cho biểu thức $\left|\overrightarrow{\mathrm{IA}}-2\overrightarrow{\mathrm{IB}}+5\overrightarrow{\mathrm{IC}}\right|$ đạt giá trị nhỏ nhất.

A. $\mathrm{I}\left(-\frac{37}{4};0;\frac{19}{4}\right)$

B. $\mathrm{I}\left(-\frac{27}{4};0;\frac{21}{4}\right)$

C. $\mathrm{I}\left(\frac{37}{4};0;-\frac{23}{4}\right)$

D. $\mathrm{I}\left(\frac{25}{4};0;-\frac{19}{4}\right)$

Câu 43: Cho hình phẳng D giới hạn bởi đồ thị các hàm số $\mathrm{y}=\sqrt{1-{\mathrm{x}}^2}$ và y = 2(1 – x). Biết thể tích khối tròn xoay được tạo thành khi quay D quanh trục Ox bằng $\frac{\mathrm{a\pi }}{\mathrm{b}}$, trong đó a và b là các số tự nhiên nguyên tố cùng nhau. Tìm a – b.

A. 71

B. ‒71

C. 2

D. ‒2

Câu 44: Biết $\underset{1}{\overset{2}{\int }}\frac{2\mathrm{dx}}{{\mathrm{x}}^3+3{\mathrm{x}}^2+2\mathrm{x}}=\ln \frac{\mathrm{a}}{\mathrm{b}}$, trong đó a và b là các số tự nhiên nguyên tố cùng nhau. Tìm a + b.

A. 59

B. 58

C. 57

D. 56

Câu 45: Cho f(x) là một hàm liên tục trên $\mathrm{ℝ}$ và a là một số thực lớn hơn 1. Mệnh đề nào dưới đây sai?

A. $\underset{0}{\overset{\mathrm{a}}{\int }}{\mathrm{x}}^3\mathrm{f}\left({\mathrm{x}}^2\right)\mathrm{dx}=\frac{1}{2}\underset{0}{\overset{{\mathrm{a}}^2}{\int }}\mathrm{xf}\left(\mathrm{x}\right)\mathrm{dx}$

B. $\underset{0}{\overset{\mathrm{\pi }}{\int }}\mathrm{xf}\left(\mathrm{sinx}\right)\mathrm{dx}=\frac{\mathrm{\pi }}{2}\underset{0}{\overset{\mathrm{\pi }}{\int }}\mathrm{f}\left(\mathrm{sinx}\right)\mathrm{dx}$

C. $\underset{-\mathrm{\pi }}{\overset{\mathrm{\pi }}{\int }}\mathrm{xf}\left(\mathrm{cosx}\right)\mathrm{dx}=0$

D. $\underset{1}{\overset{{\mathrm{a}}^2}{\int }}\frac{\mathrm{f}\left(\sqrt{\mathrm{x}}\right)}{\sqrt{\mathrm{x}}}\mathrm{dx}=\frac{1}{2}\underset{1}{\overset{\mathrm{a}}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

Câu 46: Cho $\underset{0}{\overset{\frac{1}{2}}{\int }}\sqrt{1-{\mathrm{x}}^2}\mathrm{dx}=\frac{\mathrm{\pi }}{\mathrm{a}}+\frac{\sqrt{3}}{\mathrm{b}},(\mathrm{a},\mathrm{b}\in \mathrm{N})$. Khi đó S = a + b là:

A. 15

B. 18

C. 14

D. 20

Câu 47: Cho $\underset{0}{\overset{\frac{\mathrm{\pi }}{4}}{\int }}\mathrm{f}\left(\cos 2\mathrm{x}\right).\sin 2\mathrm{x}.\mathrm{dx}=4$. Khi đó $\underset{0}{\overset{1}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$ có giá trị là:

A. 8

B. 2

C. -8

D.  - 2

Câu 48: Cho $\int \mathrm{cosx}.\mathrm{f}\left(\mathrm{x}\right).\mathrm{dx}=\mathrm{sinx}.\mathrm{f}\left(\mathrm{x}\right)-\int \mathrm{cosx}.\mathrm{dx}$. Khi đó f(x) là hàm số nào trong các hàm số sau?

A. $\mathrm{f}\left(\mathrm{x}\right)=\ln \left|\mathrm{sinx}\right|$

B. $\mathrm{f}\left(\mathrm{x}\right)=\mathrm{cotx}$

C. $\mathrm{f}\left(\mathrm{x}\right)=\mathrm{tanx}$

D. $\mathrm{f}\left(\mathrm{x}\right)=-\ln \left|\mathrm{cosx}\right|$

Câu 49: Diện tích hình phẳng giới hạn bởi các đường y = f(x), y = g(x), x = a, x = b (a > b) có công thức tính là:

A. $\mathrm{S}=\underset{\mathrm{a}}{\overset{\mathrm{b}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{dx}$

B. $\mathrm{S}=\underset{\mathrm{b}}{\overset{\mathrm{a}}{\int }}\left[\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right]\mathrm{dx}$

C. $\mathrm{S}=\underset{\mathrm{b}}{\overset{\mathrm{a}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{dx}$

D. $\mathrm{S}=\mathrm{\pi }\underset{\mathrm{b}}{\overset{\mathrm{a}}{\int }}\left|\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right|\mathrm{dx}$