TOP 10 Đề thi Học kì 2 Toán lớp 12 năm 2024 có đáp án
Bộ 10 đề thi Học kì 2 Toán lớp 12 năm 2023 - 2024 có đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 12 Học kì 2. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi Học kì 2 Toán 12 bản word có lời giải chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi Học kì 2 Toán lớp 12 năm 2023 - 2024 có đáp án
Phòng Giáo dục và Đào tạo .....
Năm học ...
Môn: Toán 12
Thời gian làm bài: 90 phút
Câu 1. Cho số phức z thỏa mãn z+3ˉz=(¯1−2i)2. Phần ảo của z là
A. 34;
B. – 2;
C. 2;
D. -34.
Câu 2. Biết f(x) là hàm liên tục trên ℝ và 9∫0f(x)dx=9. Khi đó giá trị của 4∫1f(3x−3)dx là
A. 3;
B. 27;
C. 0;
D. 24.
Câu 3. Cho1∫0x.ex−1x+1(x+1)4dx=abe−cd trong đó a, b, c, d là các số nguyên dương và ab,cd là các phân số tối giản. Giá trị của logb(da+dc) bằng
A. 6;
B. 4;
C. 2;
D. 5.
Câu 4. Tích phân 2020∫02xdx bằng:
A. 22021−2ln2;
B. 22021−ln22;
C. 22020−1ln2;
D. 22020−ln22.
Câu 5. Số phức z = 4 – 3i có môđun bằng
A. 8;
B. 2√2;
C. 5;
D. 25.
Câu 6. Trong không gian Oxyz, đường thẳng Δ:x+1−2=y−23=z−21 có một vectơ
chỉ phương là
A. →u1=(1;−2;−2);
B. →u4=(2;−3;−1);
C. →u2=(−2;−3;−1);
D. →u3=(−1;2;2).
Câu 7. Trong không gian với hệ trục Oxyz cho ba điểmA(−1;2;−3), B(1;0;2), C(x;y;−2) thẳng hàng. Khi đó x + y bằng
A. x+y=−115;
B. x+y=115;
C. x+y=1;
D. x+y=17.
Câu 8. Tìm số thực a < 0 thỏa mãn a∫1(x3−6x)dx=8754.
A. a=−6;
B. a=−3;
C. a=−4;
D. a=−5.
Câu 9. Cho hàm số f(x) xác định trên R\{1} thỏa mãn f', f(0) = 2017, f(2) =
2018. Tính S = f(3) – f(1).
A. S = 4;
B. S = 1;
C. S = ln2;
D. S = ln4035.
Câu 10. Biết , với a, b, c là các số nguyên dương. Tính P = c + b – a.
A. P = 80;
B. P = – 76;
C. P = 82;
D. P = 86.
Câu 11. Trong không gian tọa độ Oxyz, cho điểm A(3; – 2; 5). Hình chiếu vuông góc
của điểm A trên mặt phẳng tọa độ (Oxz):
A. ;
B. ;
C. ;
D. .
Câu 12. Cho số phức z = 6 + 7i. Số phức liên hợp của z là:
A. ;
B. ;
C. ;
D. .
Câu 13. Biết a là số thực thỏa mãn . Mệnh đề nào sau đây đúng?
A. ;
B. ;
C. ;
D. .
Câu 14. Trong không gian cho và . Đường thẳng đi qua hai điểm
AB có phương trình là.
A. ;
B. ;
C. ;
D. .
Câu 15. Cho biết . Tính giá trị của .
A. P = 19;
B. P = 37;
C. P = 27;
D. P = 15.
Câu 16. Cho hàm số y = f(x) liên tục trên [3; 4;]. Gọi D là hình phẳng giới hạn bởi đồ
thị hàm số y = f(x), trục hoành và hai đường thẳng x = 3, x = 4. Thể tích khối tròn xoay
tạo thành khi quay D quanh trục hoành được tính theo công thức
A. ;
B. ;
C. ;
D. .
Câu 17. Họ nguyên hàm của hàm số là
A. ;
B. ;
C. ;
D. .
Câu 18. Phương trình có hai nghiệm là . Giá trị của là
A. 6;
B. 4;
C. 2;
D. 3.
Câu 19. Cho số phức z thỏa mãn là số thực và . Phần ảo của z là:
A. 2;
B. 1;
C. – 2;
D. – 1.
Câu 20. Cho hàm số f(x) liên tục trên biết: và . Giá trị của bằng
A. 10;
B. 5;
C. 9;
D. 16.
Câu 21. Trong không gian với hệ tọa độ Oxyz, cho hai điểm , mặt
phẳng . Biết rằng khoảng cách từ A, B đến mặt phẳng (P) lần
lượt bằng 6 và 3. Giá trị của biểu thức T = a + b + c bằng
A. – 6;
B. 6;
C. – 3;
D. 3.
Câu 22. Trong không gian Oxyz, cho các vectơ , và
. Tọa độ của vectơ là
A. ;
B. ;
C. ;
D. .
Câu 23. Cho và . Khi đó bằng
A. 7;
B. 12;
C. – 12;
D. 1.
Câu 24. Trong không gian Oxyz, mặt phẳng cắt ba trục toạ độ tại
A, B, C sao cho tam giác ABC có trọng tâm . Giá trị a + c bằng
A. 5;
B. 3;
C. – 5;
D. – 3.
Câu 25. Cho số phức z có mô đun bằng . Biết rằng tập hợp điểm trong mặt phẳng
tọa độ biểu diễn các số phức là đường tròn có tâm I(a; b), bán kính
R. Tổng a + b + R bằng:
A. 7;
B. 3;
C. 5;
D. 1.
Câu 26. Cho . Khi đó bằng
A. 8;
B. 4;
C. 1;
D. 2.
Câu 27. Họ nguyên hàm của hàm số f(x) = x – sinx là
A. ;
B. ;
C. ;
D. .
Câu 28. Trong không gian Oxyz, cho mặt cầu . Tìm
tọa độ tâm I và bán kính R của (S) là
A. , ;
B. , ;
C. , ;
D. , .
Câu 29. Trong không gian Oxyz, cho đường thẳng và mặt
phẳng , phương trình đường thẳng ∆ nằm trong mặt phẳng (P),
cắt d và vuông góc với d là
A. ;
B. ;
C. ;
D. .
Câu 30. Ký hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục
hoành, đường x = a, x = b (như hình vẽ). Khẳng định nào sau đây là đúng?
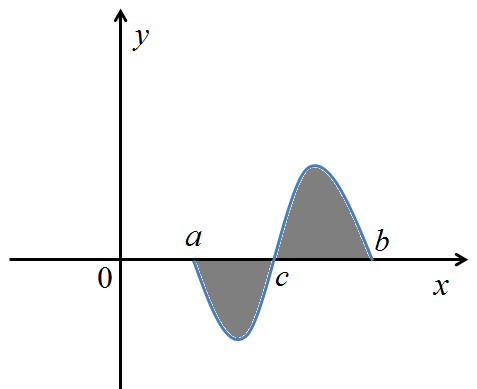
A. ;
B. ;
C. ;
D. .
Câu 31. Biết (a, b, c là các số nguyên). Giá trị a + b – c bằng
A. 3 ;
B. 2 ;
C. – 4 ;
D. – 1.
Câu 32. Cho và với có đồ thị như
hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y = f(x). Diện tích
hình phẳng giới hạn bởi hai đường cong y = f(x) và y = g(x) gần nhất với kết quả nào
dưới đây?
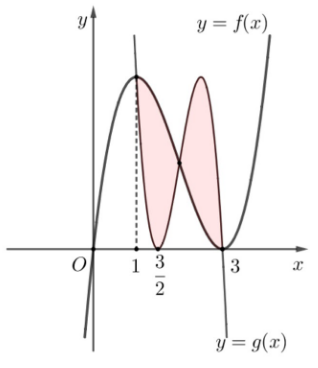
A. 3,67;
B. 4,5;
C. 4,25;
D. 3,63.
Câu 33. Nguyên hàm của hàm số là
A. ;
B. ;
C. ;
D. .
Câu 34. Cho hàm số f(x) có đạo hàm f’(x) liên tục trên [a; b], f(b) và , khi
đó f(a) bằng
A. – 6;
B. – 4;
C. 4;
D. 6.
Câu 35. Cho số phức z = 3 – 4i. Tìm phần thực và phần ảo của số phức z.
A. Phần thực là 3 và phần ảo là – 4;
B. Phần thực là – 4 và phần ảo là 3i ;
C. Phần thực là – 4 và phần ảo là 3 ;
D. Phần thực là 3 và phần ảo là – 4i.
Câu 36. Biết số phức z = –3 + 4i là một nghiệm của phương trình , trong
đó a, b là các số thực. Tính a – b.
A. – 11 ;
B. 1 ;
C. – 31 ;
D. – 19.
Câu 37. Cho tích phân trong đó a, b là các số nguyên dương. Tổng a + b2 bằng
A. 8;
B. 16;
C. 20;
D. 12.
Câu 38. Cho số phức z, w khác 0 thỏa mãn và . Khi đó bằng:
A. ;
B. 3;
C. ;
D. .
Câu 39. Biết rằng có duy nhất 1 cặp số thực (x; y) thỏa mãn .
Tính S = x + 2y.
A. S = 4;
B. S = 3;
C. S = 5;
D. S = 6.
Câu 40. Biết , trong đó a, b, m, n là các số nguyên dương. Giá trị của biểu thức (a + b)(m + n) bằng
A. 40;
B. 36;
C. 72;
D. 42.
Câu 41. Trong không gian Oxyz, mặt phẳng đi qua 3 điểm A(1; 0; 0), B(0; 2; 0), C(0;
0; 3) có phương trình là
A. ;
B. ;
C. ;
D. .
Câu 42. Tích phân bằng
A. ;
B. ;
C. 1;
D. .
Câu 43. Gọi z1, z2 là hai trong các số phức z thỏa mãn và .
Tìm môđun của số phức .
A. ;
B. ;
C. ;
D. .
Câu 44. Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua
hai điểm , và vuông góc với mặt phẳng (Q): x + y + z = 0.
A. ;
B. ;
C. ;
D. .
Câu 45. Trong không gian Oxyz, đường thẳng ∆ đi qua và nhận véc tơ
làm véctơ chỉ phương có phương trình chính tắc là:
A. ;
B. ;
C. ;
D. .
Câu 46. Trong không gian Oxyz, phương trình đường thẳng đi qua A(1; 2; 4) song
song với (P): và cắt đường thẳng
d:có phương trình:
A. ;
B. ;
C. ;
D. .
Câu 47. Trong mặt phẳng Oxy, điểm nào sau đây biểu diễn số phức z = 2 + i?
A. ;
B. ;
C. ;
D. .
Câu 48. Cho . Tính tích phân .
A. ;
B. ;
C. ;
D. I = 2.
Câu 49. Trong không gian Oxyz, mặt phẳng , (P) đi qua điểm nào
dưới đây?
A. ;
B. ;
C. ;
D. .
Câu 50. Trong không gian với hệ trục tọa độ Oxyz, cho điểm .
Mặt cầu (S) có tâm I thuộc Ox và đi qua hai điểm A, B có phương trình.
A. ;
B. ;
C. ;
D. .
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 12
Thời gian làm bài: 90 phút
Đề thi Toán lớp 12 Học kì 2 đề số 2
Câu 1. Tìm một nguyên hàm F(x) của hàm số biết F(3) = 10.
A.;
B.;
C.;
D..
Câu 2. Trong không gian Oxyz, cho hai điểm A(2; 1; 2) và B(0; 1; 4). Tìm tọa độ điểm
M trên mặt phẳng tọa độ (Oxy) sao cho nhỏ nhất.
A. M(– 2; 2; 0);
B. M(– 1; 1; 0);
C. M(2; – 2; 0);
D. M(1; 1; 0).
Câu 3. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thỏa mãn điều kiện
|z – i| = 4 là một đường tròn có tâm I và bán kính R là
A. I(1; 0) và R = 2 ;
B. I(–1; 0) và R = 4 ;
C. I(0; –1) và R = 2 ;
D. I(0; 1) và R = 4.
Câu 4. Trong không gian Oxyz cho tam giác ABC có A(1; 0; 0), B(0; –2; 3), C(1; 1;
1). Phương trình mặt phẳng (P) chứa A, B sao cho khoảng cách từ C tới (P) là .
A. x + y + z – 1 = 0 hoặc – 23x + 37y + 17z + 23 = 0;
B. 2x + 3y + z – 1 = 0 hoặc 3x + y + 7z + 6 = 0;
C. x + 2y + z – 1 = 0 hoặc – 2x + 3y + 6z + 13 = 0;
D. x + y + 2z – 1 = 0 hoặc – 2x + 3y + 7z + 23 = 0.
Câu 5. Kết quả của tích phân
A. K = ln2;
B. K = 2ln2;
C. ;
D. .
Câu 6. Trong không gian Oxyz, cho ba điểmvà. Tìm tọa
độ điểm Q để tứ giác MNPQ là hình bình hành.
A.;
B.;
C.;
D..
Câu 7. Cho hai mặt phẳng (P) và (Q) có phương trình lần lượt là: 2x – y + z = 0 và 2x
– y + z – 7 = 0. Khoảng cách giữa hai mặt phẳng trên là:
A.;
B.;
C. 7;
D. .
Câu 8. Hàm số là nguyên hàm của hàm số f(x) nào
A. ;
B. ;
C.;
D..
Câu 9. Trong không gian Oxyz, cho mặt phẳng (P): x + 2y + 3z – 1 = 0. Vectơ nào
dưới đây là một vectơ pháp tuyến của (P)?
A. ;
B. ;
C. ;
D. .
Câu 10. Cho A(–1; 2; 1), B(–4 ; 2; –2), C(–1; –1; –2). Viết phương trình tổng quát của
mp(ABC).
A. (ABC): 2x + y – 2z + 2 = 0;
B. (ABC): x – y + 3z = 0;
C. (ABC): 2x + y + z – 1 = 0;
D. (ABC): x + y – z = 0.
Câu 11. Trong không gian với hệ tọa độ Oxyz. Cho các vectơ
. Tìm tọa độ của vectơ , biết:
A.(2; 4; 3) ;
B.(2; 3; 4) ;
C.(–5; –7; 0) ;
D.(5; 7; 1).
Câu 12. Điểm biểu diễn số phức có tọa độ là
A. (1; 4) ;
B.(–1; 4) ;
C.(–1; –4) ;
D.(1; –4).
Câu 13. Trong không gian Oxyz, cho hai vectơ , tạo với nhau góc v
. Khi đó, bằng:
A.;
B.;
C. ;
D. 2.
Câu 14. Biết F(x) là một nguyên hàm của hàm số và F(0) = 5e. Tính F(3).
A. ;
B.;
C.;
D..
Câu 15. Số phức z thỏa mãn: là
A. –3 – 2i ;
B. –3 + 2i ;
C. 3 – 2i ;
D. 3 + 2i.
Câu 16. Cho số phức và . Môđun số phức là
A.;
B. 8;
C.;
D. 4.
Câu 17. Cho hình phẳng (H) giới hạn bởi đường thẳng y = x ; trục hoành và đường thẳng x
= m, m > 0. Thể tích khối tròn xoay tạo bởi khi quay (H) quanh trục hoành là (đvtt).
Giá trị của tham số m là :
A. 3 ;
B. 6 ;
C. 9 ;
D. 1.
Câu 18. Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A'B'C' có A(1; 1; 1),
B(1; 2; 1), C(1; 1; 2) và A’(2; 2; 1). Viết phương trình mặt cầu đi qua bốn điểm A, B,
C, A'?
A. x2 + y2 + z2 – 3x – 3y – 3z – 6 = 0;
B. x2 + y2 + z2 – 3x – 3y – 3z + 6 = 0;
C. x2 + y2 + z2 + 3x – 3y – 3z + 6 = 0;
D. x2 + y2 + z2 – 3x – 3y + 3z + 6 = 0
Câu 19. Khẳng định nào sau đây sai ?
A.
B.
C.;
D.
Câu 20. Mặt cầu (S) có tâm I(1; 2; –3) và đi qua A(1; 0; 4) có phương trình
A. (x + 1)2 + (y + 2)2 + (z + 3)2 = 53;
B. (x – 1)2 + (y – 2)2 + (z – 3)2 = 53;
C. (x + 1)2 + (y + 2)2 + (z – 3)2 = 53;
D. (x – 1)2 + (y – 2)2 + (z + 3)2 = 53;
Câu 21. Cổng của trường ĐHBK Hà nội có hình dạng Parabol, chiều rộng 8m, chiều
cao 12,5m . Diện tích của cổng là
A.
B.
C.
D.
Câu 22. Trong không gian Oxyz, mặt cầu có tâm trên trục Ox và tiếp xúc với hai mặt
phẳng x + 2y – 2z + 5 = 0 và 3x – 2y + 6z – 7 = 0 có phương trình là:
A. ;
B. ;
C. ;
D. .
Câu 23. Trong không gian Oxyz, gọi là mặt phẳng cắt ba trục tọa độ tại ba điểm
, ,. Phương trình của là:
A.;
B.;
C.;
D..
Câu 24. Số phức z thỏa mãn: . Vậy môđun của số phức z là
A.;
B.;
C. 1;
D. 3.
Câu 25. Cho số phức z thỏa |z – 3 + 4i | = 2 và w = 2z + 1 – i. Trong mp phức, tập hợp
điểm biểu diễn số phức w là đường tròn tâm I, bán kính R với:
A. I(3; –4) ; R = 2;
B. I(4; –5) ; R = 4;
C. I(5; –7) ; R = 4;
D. I(7; –9) ; R = 4.
Câu 26. Gọi A, B, C lần lượt là các điểm biểu diễn các số phức: . Ta có:
A.Tam giác ABC không cân;
B.Tam giác ABC không vuông;
C.Tam giác ABC vuông cân;
D.Tam giác ABC là tam giác đều.
Câu 27. Một vật chuyển động với vận tốc 10 (m/s) thì tăng tốc với gia tốc a(t)=3t + t2
(m/s2). Tính quãng đường vật đi được trong khoảng thới gian 6 giây kể từ lúc bắt đầu
tăng tốc.
A. 267 (m);
B.(m);
C.(m);
D. 276 (m).
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
. Tính bán kính R của (S).
A.;
B. R = 8;
C. R = 4;
D. R = 64.
Câu 29. Trong không gian đối với một hệ trục Oxyz. Cho A(–2; 3; 8) , điểm A' đối
xứng với A qua mp(Oxz) có toạ độ là :
A. (–2; 3; –8);
B. (–2; –3; 8);
C. (2; 3; 8);
D. (2; –3; –8).
Câu 30. Điểm M trong hình vẽ bên là điểm biểu diễn số phức
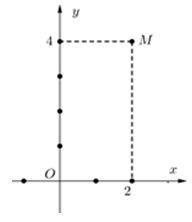
A.;
B.;
C.;
D..
Câu 31. Gọi F(x) là một nguyên hàm của hàm số f(x) = ln(x + 2) mà F(–1) = 2 , giá trị
F(0) bằng:
A. 4ln2 + 1;
B. 2ln2 + 1;
C. 5ln2 + 1;
D. 3ln2 + 1.
Câu 32. Cho và . Tính
A. –8;
B. –4;
C. 7;
D. 4.
Câu 33. Diện tích hình phẳng giới hạn bởi các đường thẳng và trục
tung bằng
A.;
B.;
C.;
D..
Câu 34. Diện tích hình phẳng giới hạn bởi các đường: y = x2 +3 và y = 4x là:
A.;
B.;
C.;
D..
Câu 35. Biết rằng tích phân, tích 4ab bằng:
A. 2;
B. 3;
C. 1;
D. 4.
Câu 36. Cho số phức . Tìm số phức w =1+ z + z2
A.;
B. 0 ;
C.;
D. 1.
Câu 37. Trong không gian Oxyz, cho hai mặt phẳng và
. Tìm các giá trị của m, n để hai mặt phẳng và song
song với nhau.
A.;
B.;
C.;
D..
Câu 38. Tích phân bằng:
A.;
B.;
C.;
D..
Câu 39. Nếu với a, b thuộc Q thì a + 2b bằng:
A. 1;
B. 2;
C. ;
D. .
Câu 40. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thỏa mãn điều
kiện là:
A. Đường tròn;
B. Elip;
C. Hypebol;
D. Parabol.
Câu 41. Cho số phức: . Khi đó giá trị môdun của là:
A. 1 ;
B. 5 ;
C. 4 ;
D. 2.
Câu 42. Cho 2 điểm A(2; 4; 1), B(–2; 2; –3). Phương trình mặt cầu đường kính AB là:
A. x2 + (y – 3)2 + (z + 1)2 = 3 ;
B. x2 + (y – 3)2 + (z – 1)2 = 9 ;
C. x2 + (y + 3)2 + (z – 1)2 = 9 ;
D. x2 + (y – 3)2 + (z + 1)2 = 9.
Câu 43. Cho f(x) liên tục trên đoạn [0; 10] thỏa mãn
Khi đó giá trị của là:
A. 10;
B. 1;
C. 4043;
D. –1.
Câu 44. Một vật thể không gian giới hạn bởi hai mặt phẳng x = a, x = b. Một mặt
phẳng tùy ý vuông góc với trục Ox tại điểm x (a ≤ x ≤ b) cắt vật theo thiết diện là một
hình vuông có đường chéo bằng . Thể tích của vật bằng
A.;
B.;
C.;
D.
Câu 45. Diện tích hình phẳng phần bôi đen trong hình sau được tính theo công thức:

A.;
B.;
C.;
D..
Câu 46. Cho biết, với a, b là các số nguyên dương. Giá trị của a, b là
A. 12;
B. 18;
C. 11;
D. 13.
Câu 47. Trong không gian Oxyz, cho điểm A(3; –1; 1). Hình chiếu vuông góc của A
trên mặt phẳng (Oxz) là điểm
A.;
B.;
C.;
D..
Câu 48. Cho hàm số f(x) có đạo hàm liên tục trên và thỏa mãn và f(0) = 9. Tích phân bằng
A. I = 2013;
B. I = 2031;
C. I = 2030;
D. I = 2011.
Câu 49. Cho số phức z = 3 – 4i. Phần thực và phần ảo của số phức liên hợp là
A. Phần thực bằng 3 và phần ảo bằng 4;
B. Phần thực bằng 3 và phần ảo bằng – 4i;
C. Phần thực bằng 3 và phần ảo bằng – 4;
D. Phần thực bằng 3 và phần ảo bằng 4i.
Câu 50. Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục Ox, đường thẳng x = a, x = b (a < b) là:
A.;
B.;
C.;
D..
Để xem trọn bộ Đề thi Toán 12 có đáp án, Thầy/ cô vui lòng Tải xuống!
Xem thêm các chương trình khác:
- Góp ý sgk lớp 12 tất cả các môn năm 2024 - 2025 (3 bộ sách)
- Đề thi chính thức các môn THPT Quốc Gia các năm
- (3000+) Đề thi thử THPT Quốc Gia (các năm) từ các trường, sở trên cả nước
- Đề minh họa THPT quốc gia các năm
- Đề thi Đánh giá năng lực năm 2023 | Thông tin | Cấu trúc ĐGNL ĐHQG Hà Nội, HCM, ĐHBK, Bộ Công an
