Câu hỏi:
23/07/2024 1,290Cho hình chóp S.ABC có SA = SB = SC = BA = BC = 1. Tìm thể tích lớn nhất của khối chóp S.ABC?
A. 16
B. √212
C. 18
D. √312
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C.
Cách 1:
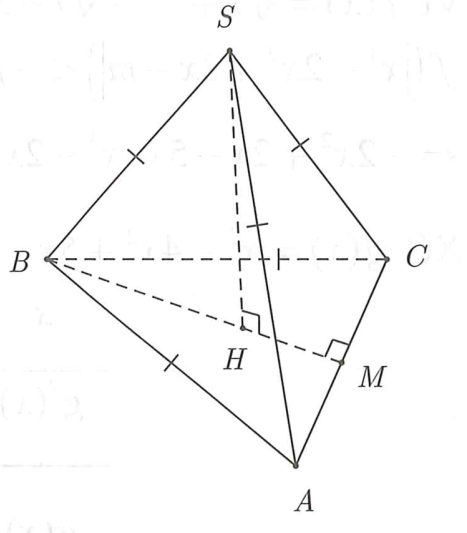
Gọi H là hình chiếu của S lên (ABC).
Khi đó H là tâm đường tròn ngoại tiếp
Vì ΔABC cân tại B nên H thuộc đường trung trực BM của AC.
Đặt AC =
Ta có: SΔABC=12.BM.AC=12.x.√1−x24=x√4−x24 và R=abc4SΔABC=1√4−x2.
Chiều cao của khối chóp là: SH=√SB2−BH2=√SB2−R2=√3−x24−x2.
Thể tích khối chóp là: V=13.SH.SΔABC=13.√3−x24−x2.x√4−x24=√x2(3−x2)12.
Theo bất đẳng thức Côsi ta có: √x2(3−x2)≤√(x2+3−x2)24=32.
Do đó V=√x2(3−x2)12≤32.12=18.
Dấu “=” xảy ra khi và chỉ khi x2=3−x2⇔x=√32.
Cách 2:
Gọi K, I lần lượt là hình chiếu của C lên (SAB) và SB.
Thể tích khối chóp: V=13.CK.SSAB≤13.CI.SSAB.13.√32.√34=18.
Dấu “=” xảy ra khi và chỉ khi hình chiếu của C lên (SAB) trùng trung điểm SB.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Cho phương trình 2(x−1)2.log2(x2−2x+3)=4|x−m|.log2(2|x−m|+2) với m là tham số thực. Tìm tất cả các giá trị của m để phương trình có đúng hai nghiệm phân biệt.
Câu 5:
Cho hàm số bậc bốn y = f(x) có đồ thị như hình vẽ dưới đây.
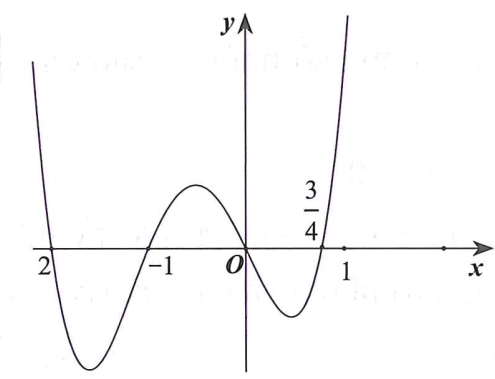
Số điểm cực trị của hàm số g(x)=f(2x3+3x2) là
Câu 7:
Cho các số thực a, b (với a < b). Nếu hàm số y = f(x) có đạo hàm là hàm liên tục trên thì
Câu 8:
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A(1;2;-3) có vectơ pháp tuyến →n=(2;−1;3) là
Câu 10:
Hệ thức liên hệ giữa giá trị cực đại và giá trị cực tiểu của hàm số y=x3−2x là
Câu 11:
Phương trình bậc hai nào dưới đây nhận hai số phức 2 - 3i và 2 + 3i làm nghiệm?
Câu 13:
Cho hàm số y=x2−m2+2m+1x−m (với m là tham số). Tìm tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên từng khoảng xác định.
Câu 14:
Một thùng đựng thư được thiết kế như hình vẽ bên, phần phía trên là nửa hình trụ. Thể tích của thùng đựng thư bằng
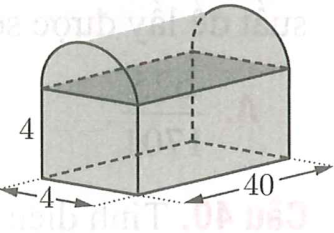
Câu 15:
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ →a=(2;−3;1) và →b=(−1;4;−2). Giá trị của biểu thức →a.→b bằng



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)