Câu hỏi:
12/07/2024 221
Cho hàm số f(x) = ax2 + bx + c (a, b, c ≠ 0) có đồ thị như hình vẽ bên.
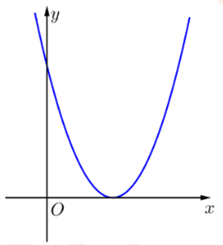
Biết f(c) = c. Giá trị của b là:
Cho hàm số f(x) = ax2 + bx + c (a, b, c ≠ 0) có đồ thị như hình vẽ bên.

Biết f(c) = c. Giá trị của b là:
A. b = –6;
B. b = –2;
C. \(b = - \frac{5}{2}\);
D. b = –4.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Quan sát đồ thị, ta thấy parabol cắt trục hoành tại đỉnh của parabol hay parabol cắt trục hoành tại một điểm duy nhất.
Nghĩa là, phương trình ax2 + bx + c = 0 có nghiệm kép.
Do đó ∆ = 0.
Suy ra b2 – 4ac = 0 (1)
Ta có f(c) = c.
Suy ra ac2 + bc + c = c.
Khi đó c(ac + b) = 0.
Vì vậy ac + b = 0 (vì c ≠ 0).
Do đó \(c = - \frac{b}{a}\) (vì a ≠ 0).
Thay \(c = - \frac{b}{a}\) vào (1) ta được: \({b^2} - 4.a.\left( { - \frac{b}{a}} \right) = 0\).
Khi đó b2 + 4b = 0 Û b(b + 4) = 0.
Vì vậy b = 0 hoặc b = –4.
Vì b ≠ 0 nên ta nhận b = –4.
Vậy ta chọn phương án D.
Hướng dẫn giải
Đáp án đúng là: D
Quan sát đồ thị, ta thấy parabol cắt trục hoành tại đỉnh của parabol hay parabol cắt trục hoành tại một điểm duy nhất.
Nghĩa là, phương trình ax2 + bx + c = 0 có nghiệm kép.
Do đó ∆ = 0.
Suy ra b2 – 4ac = 0 (1)
Ta có f(c) = c.
Suy ra ac2 + bc + c = c.
Khi đó c(ac + b) = 0.
Vì vậy ac + b = 0 (vì c ≠ 0).
Do đó \(c = - \frac{b}{a}\) (vì a ≠ 0).
Thay \(c = - \frac{b}{a}\) vào (1) ta được: \({b^2} - 4.a.\left( { - \frac{b}{a}} \right) = 0\).
Khi đó b2 + 4b = 0 Û b(b + 4) = 0.
Vì vậy b = 0 hoặc b = –4.
Vì b ≠ 0 nên ta nhận b = –4.
Vậy ta chọn phương án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Đồ thị hàm số y = mx2 – 2mx – m2 – 2 (m ≠ 0) là parabol có đỉnh nằm trên đường thẳng y = x – 3 thì m nhận giá trị nằm trong khoảng nào dưới đây?
Câu 2:
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt giá trị nhỏ nhất bằng 4 tại x = 2 và có đồ thị đi qua điểm A(0; 6). Giá trị biểu thức P = abc bằng
Câu 3:
Một chiếc cổng hình parabol có phương trình \(y = - \frac{1}{2}{x^2}\). Biết cổng có chiều rộng d = 5 m. Chiều cao h của cổng bằng:
Câu 4:
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học phát hiện ra rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ có cân nặng P(n) = 360 – 10n. Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lượng cá sau một vụ thu được nhiều nhất?


