Cho định lí “Nếu hai tam giác bằng nhau thì diện tích chúng bằng nhau”. Mệnh đề nào sau đây đúng?

Đáp án đúng là: D

* Lời giải

- Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau.

$\to$D đúng, A sai.

- Hai tam giác có diện tích bằng nhau là điều kiện cần đề chúng bằng nhau.

$\to$ C sai.

- Hai tam giác có diện tích bằng nhau nhưng chưa chắc đã bằng nhau nên không thể là điều kiện cần và đủ để chúng bằng nhau.

$\to$B sai.

* Phương pháp giải

- Cho định lí P $\Rightarrow$ Q ta nói:

+ "P là điều kiện đủ để có Q" hoặc Q là điều kiện cần để có P"

+ "P là điều kiện cần và đủ để có Q" nếu mệnh đề P $\iff$Q đúng.

*Một số lý thuyết nắm thêm về mệnh đề: 

1. Mệnh đề toán học

• Mệnh đề toán học là mệnh đề khẳng định một sự kiện trong toán học.

2. Mệnh đề chứa biến

• Ở mệnh đề chứa biến, ta chưa thể khẳng định ngay tính đúng hoặc sai. Với mỗi giá trị cụ thể của biến số, ta có một mệnh đề toán học mà ta có thể khẳng định tính đúng hoặc sai của mệnh đề.

Kí hiệu mệnh đề chứa biến n là P(n), mệnh đề chứa biến x, y là P(x, y), …

Ví dụ:

+ P(x): “x là một số nguyên tố” là một mệnh đề chứa biến

3. Phủ định của một mệnh đề

• Cho mệnh đề P. Mệnh đề “Không phải P” được gọi là mệnh đề phủ định của mệnh đề P và kí hiệu là $\overline{P}$.

Mệnh đề $\overline{P}$ đúng khi P sai, và ngược lại.

Ví dụ:

+ A: “69420 là một số lẻ” là mệnh đề sai.

Mệnh đề phủ định $\overline{A}$: “69420 không phải một số lẻ”, $\overline{A}$ là mệnh đề đúng.

Chú ý: Để phủ định một mệnh đề, ta chỉ cần thêm (hoặc bớt) từ “không” (hoặc “không phải”) vào trước vị ngữ của mệnh đề đó.

4. Mệnh đề kéo theo

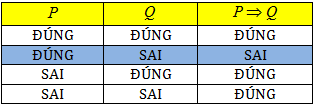
• Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, được kí hiệu là P ⇒ Q.

Mệnh đề P ⇒ Q chỉ sai khi P đúng Q sai, và đúng trong tất cả các trường hợp còn lại.

Nhận xét: Tùy theo nội dung cụ thể, đôi khi người ta còn phát biểu mệnh đề P ⇒ Q là “P kéo theo Q” hay “P suy ra Q” hay “Vì P nên Q”…

Ví dụ:

+ Xét hai mệnh đề: P: “Tứ giác ABCD có bốn cạnh bằng nhau” và Q: “Tứ giác ABCD là hình thoi”.

+ Mệnh đề P ⇒ Q được phát biểu là: “Nếu tứ giác ABCD có bốn cạnh bằng nhau thì tứ giác ABCD là hình thoi”. Mệnh đề này là mệnh đề đúng.

Nhận xét: Các định lí toán học thường phát biểu ở dạng mệnh đề kéo theo P ⇒ Q.

Khi đó ta nói:

P là giả thiết, Q là kết luận của định lí, hay P là điều kiện đủ để có Q, hoặc Q là điều kiện cần để có P.

5. Mệnh đề đảo. Mệnh đề tương đương

• Mệnh đề Q ⇒ P là mệnh đề đảo của mệnh đề P ⇒ Q.

Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều đúng, P và Q là hai mệnh đề tương đương và kí hiệu P ⇔ Q.

Nhận xét: Mệnh đề P ⇔ Q có thể phát biểu ở những dạng như sau:

+ “P tương đương Q”;

+ “P là điều kiện cần và đủ để có Q”;

+ “P khi và chỉ khi Q”;

+ “P nếu và chỉ nếu Q”.

6. Kí hiệu ∀ và ∃

• Kí hiệu ∀ đọc là “với mọi”.

• Kí hiệu ∃ đọc là “tồn tại”, hoặc “có một” (tồn tại một), hoặc “có ít nhất một” (tồn tại ít nhất một).

Ví dụ: Phát biểu các mệnh đề:

+ “$\forall x\in ℝ,x^2+1>0$”: Với mọi số thực x thì x² + 1 luôn lớn hơn 0.

+ “$\exists x\in \mathbb{N},2x=3$”: Tồn tại số tự nhiên x sao cho 2x bằng 3.

• Phủ định của mệnh đề “$\forall x\in X,P\left(x\right)$” là mệnh đề “$\exists x\in X,\overline{P\left(x\right)}$”.

• Phủ định của mệnh đề “$\exists x\in X,P\left(x\right)$” là mệnh đề “$\forall x\in X,\overline{P\left(x\right)}$”.

Xem thêm các bài viết hay, chi tiết khác:

Lý thuyết Toán 10 Bài 1: Mệnh đề - Kết nối tri thức

Giải SBT Toán lớp 10 Bài 1: Mệnh đề - Kết nối tri thức