Nội dung bài viết

    Xem thêm

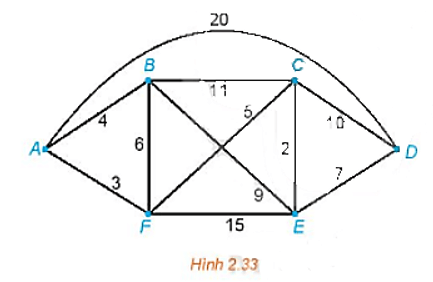
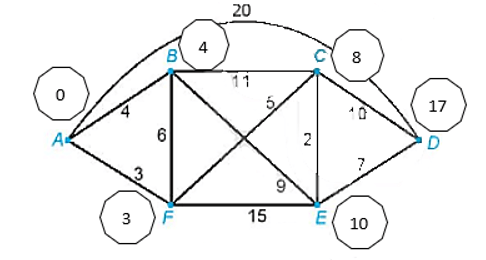
    Tìm đường đi ngắn nhất từ A đến D trong đồ thị có trọng số trên Hình 2.33

    Lời giải Bài 2.15 trang 49 Chuyên đề Toán 11 sách Chuyên đề học tập Toán lớp 11 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập.

    1 557 03/07/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Chuyên đề Toán 11 Kết nối tri thức Bài 10: Bài toán tìm đường tối ưu trong một vài trường hợp đơn giản

    Bài 2.15 trang 49 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ A đến D trong đồ thị có trọng số trên Hình 2.33.

    Bài 2.15 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức

    Lời giải:

    Đầu tiên, ta gắn nhãn đỉnh A là I(A) = 0 và gắn cho ba đỉnh kề với A là B, F và D các nhãn tạm thời I(A) + 4, I(A) + 3 và I(A) + 20. Chọn số nhỏ nhất trong chúng và viết I(F) = 3. Đỉnh F bây giờ được gắn nhãn vĩnh viễn là 3.

    Tiếp theo, ta gắn cho các đỉnh kề với F là B, C và E các nhãn tạm thời I(F) + 6, I(F) + 5 và I(F) + 15 (B hiện có hai nhãn tạm thời là 4 và 9). Nhãn tạm thời nhỏ nhất trong các nhãn đã gán (ở B, C, E) hiện nay là 4 (tại B), nên ta viết I(B) = 4. Đỉnh B được gắn nhãn vĩnh viễn là 4.

    Bây giờ ta xét các đỉnh kề với B (mà chưa được gắn nhãn vĩnh viễn) là C và E. Ta gắn cho đỉnh C nhãn tạm thời là I(B) + 11 (hiện C có hai nhãn tạm thời là 8 và 15), gắn cho đỉnh E nhãn tạm thời là I(B) + 9 (E hiện có hai nhãn tạm thời là 18 và 13. Nhãn tạm thời nhỏ nhất bây giờ là 8 (tại C), do đó ta viết I(C) = 8.

    Bây giờ ta xét các đỉnh kề với C (mà chưa được gắn nhãn vĩnh viễn) là E và D. Ta gắn nhãn cho đỉnh E tạm thời là I(C) + 2 (hiện E có ba nhãn tạm thời là 18, 13 và 10), gắn cho đỉnh D nhãn tạm thời là I(C) + 10. Nhãn tạm thời nhỏ nhất bây giờ là 10 (tại E), do đó ta viết I(E) = 10.

    Xét đỉnh kề với E là D, ta gắn cho D nhãn tạm thời I(E) + 7 (hiện D có hai nhãn tạm thời là 18 và 17). Vậy đỉnh D sẽ được gắn nhãn vĩnh viễn là 17 hay I(D) = 17.

    Vì I(D) = 17 nên đường đi ngắn nhất từ A đến D có độ dài là 17.

    Bài 2.15 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức

    Để tìm một đường đi ngắn nhất từ A đến D như vậy, ta sẽ lần ngược từ điểm cuối D. Ta chỉ cần giới hạn ở việc xét những cạnh mà độ dài là hiệu của các nhãn gắn tại đầu các mút của nó, đó là DE, EC, CF và FA (do I(D) – I(E) = 17 = 10 = 7, I(E) – I(C) = 10 – 8 = 2, I(C) – I(F) = 8 – 3 = 5 và I(F) – I(A) = 3 – 0 = 3).

    Khi đó ta có thể kết luận, đường đi ngắn nhất từ A đến D phải đi qua các cạnh DE, EC, CF và FA.

    Vậy, đường đi ngắn nhất (trong trường hợp này là duy nhất) từ A đến D là

    A → F → C → E → D.

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

    HĐ trang 46 Chuyên đề Toán 11: Cho sơ đồ như trên Hình 2.28, ở đó A, B, C, D, E, F là các địa điểm nối với nhau...

    Luyện tập trang 49 Chuyên đề Toán 11: Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.32.

    Bài 2.15 trang 49 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ A đến D trong đồ thị có trọng số trên Hình 2.33.

    Bài 2.16 trang 49 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ đỉnh S đến  mỗi đỉnh khác của đồ thị có trọng số trên Hình 2.34.

    Bài 2.17 trang 49 Chuyên đề Toán 11: Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.35.

    Bài 2.18 trang 49 Chuyên đề Toán 11: Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.36.

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

    Bài 7: Phép đồng dạng

    Bài tập cuối chuyên đề 1

    Bài 8: Một vài khái niệm cơ bản

    Bài 9: Đường đi Euler và đường đi Hamilton

    Bài tập cuối chuyên đề 2

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 557 03/07/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: